Тела вращения.
Телом вращения называется такое тело, которое плоскостями, перпендикулярными некоторой прямой (оси вращения), пересекается по кругам с центрами на этой прямой.
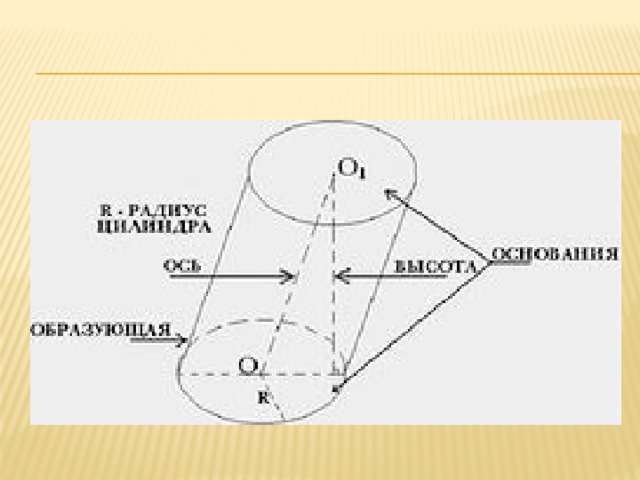
Цилиндр - это тело, которое состоит из двух кругов, не лежащих в одной плоскости и совмещаемых параллельным переносом, и всех отрезков, соединяющих соответствующие точки этих кругов.
Площадь боковой поверхности цилиндра равна произведению длины окружности основания на высоту.
S=2*π*r*h
где r – радиус цилиндра, а h – его высота.

Объём цилиндра равен произведению площади основания на высоту.
V = S*H.
V = πr2 * H.
Конус – это тело, которое состоит из круга (основания конуса), точки, не лежащей в плоскости этого круга (вершины конуса) и всех отрезков, соединяющих вершину конуса с точками основания.
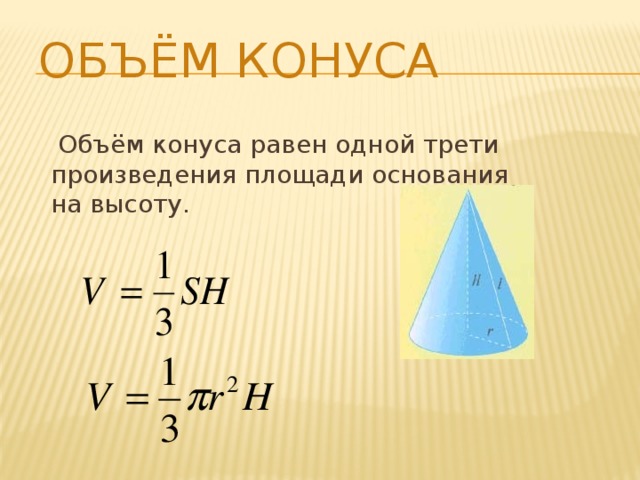
Объём конуса равен одной трети произведения площади основания на высоту.

 Получите свидетельство
Получите свидетельство Вход
Вход






















 Презентация к уроку математики "Тела вращения" (0.24 MB)
Презентация к уроку математики "Тела вращения" (0.24 MB)
 0
0 1053
1053 74
74 Нравится
0
Нравится
0


