Сценарий и презентация для внеклассного мероприятия по матемтаике "Замечательные кривые"

1. Рассмотреть конические сечения: гиперболу параболу эллипс; их определения способы построения как следа точки. Познакомить с другими  замечательными кривыми.

 2. Развивать кругозор любознательность умение видеть применение математических понятий в профессии и жизни.

 3. Воспитывать сознательное отношение к учёбе и образованию. Показать  красоту предмета.

Задачи:

1. Познакомить обучающихся с биографиями ученых : Якоба Бернулли, Рене Декарта, Фридриха Гюйгенса, их достижениями. Показать презентацию «Замечательные кривые».

 2. Построить эллипс, параболу, гиперболу как след движущейся точки, рассмотреть свойства этих линий и применение их в технике, в жизни.

 3. Провести оптические опыты с параболическим и гиперболическим зеркалами, опыт с размешиванием чая в стакане.

 4. Показать применение замечательных кривых в кондитерском деле.

Оборудование: компьютерная коммуникативная установка, планшеты для рисования кривых, параболические зеркала, гиперболическое зеркало, бусы, свеча, стакан с чаем и палочкой для размешивания, муляжи тортов и фрагменты украшения тортов.

Оформление доски: тема: «Замечательные кривые», дата, эпиграф « Математика далеко не скучная и не сухая наука. Есть в математике нечто,

 вызывающее человеческий восторг».

 Три чертежа двухполостного конуса с эллиптическим, параболическим и гиперболическим сечениями.

Ход мероприятия:

Организационный момент.

Вступление

 Мы в настоящее время изучаем на геометрии тела вращения, их свойства. Одним из тел вращения является конус. Мы рассматриваем конус как остроконечное круглое тело. На самом деле конус состоит из двух центрально - симметричных полостей. Если пересекать конус какой - либо плоскостью, то сечение будет иметь круглую, либо эллиптическую, либо параболическую, либо гиперболическую форму.

 На сегодняшнем уроке мы рассмотрим очень интересные свойства этих кривых и познакомимся с другими линиями, которые называются в математике замечательными кривыми.

 3. Показ слайдов с комментариями учителя.

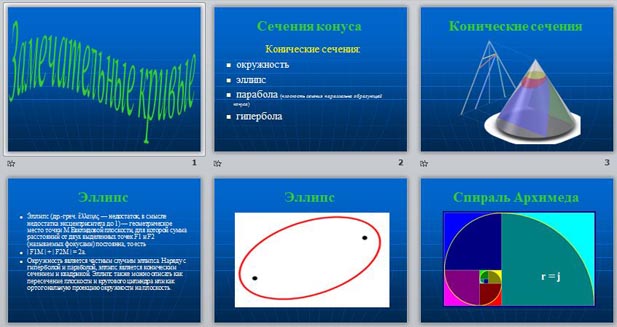
СПИРАЛЬ АРХИМЕДА.

 Архимед – ок. 287 - 212 гг. до н. э.

Родом из Сиракуз (Сицилия), сделал открытия в математике, физике, инженерном деле.

Изобретения: Архимедов винт, определение состава сплавов взвешиванием в воде, система для поднятия тяжестей, военная метательная машина.

Форма спирально завитой раковины привлекла внимание Архимеда. Он изучал эту кривую и вывел ее формулу. В настоящее время спираль А. широко используется в технике и очень распространена в природе. Раковина улитки закручена по спирали. Небольшая 10 - сантиметровая раковина имеет спираль длиной 35 см - это длина небольшой змеи. Где ее можно наблюдать? Представьте, что по радиусу равномерно вращающегося диска ползет муха. Путь, описанный мухой - это и есть С. А.

Звуковая дорожка грампластинки идет по А. спирали. Если в центр вращающейся пластинки положить натертый мелом шарик, то он, скатываясь, будет оставлять след в виде А. спирали.

 ЦИКЛОИДА ( греч. цикл - круг, идос - вид)

След, оставляемый точкой окружности, катящейся без скольжения по прямолинейной поверхности.

Можно представить как траекторию катафота, прикрепленного к ободу велосипедного колеса.

Трохоида - циклоида с избытком (трохос - колесо)

 ЛЕМНИСКАТА БЕРНУЛЛИ ( лемниската - украшенный лентами - лат. )

Якоб Бернулли - швейцарский математик из г. Базель.

XVII век. Ему принадлежат значительные достижения в дифференциальном исчислении и теории чисел, но главная его заслуга в том, что он сформулировал и доказал частный случай важнейшей теоремы теории вероятностей - закона больших чисел. Описал свойства лемнискаты.

 ЛОГАРИФМИЧЕСКАЯ СПИРАЛЬ.

Рене Декарт - франц. математик философ и естествоиспытатель построил и вывел формулу отличной от Арх. Спирали.

Луч, выходящий из центра спирали пересекает ее витки под одним и тем же углом. Это ее свойство используется в режущих станках, спираль так нравилась Я. Бернулли, что он завещал высечь ее на своей могиле.

Декартов лист.

Различные виды циклоид: гипоциклоиды, эпициклоиды - след точки окружности, катящейся по внутренней или наружной поверхности другой окружности (гипо - над, эпи - внутри)

Астроида - след точки окружности, катящейся без скольжения по внутренней поверхности окружности вчетверо большего радиуса. Если радиус окружности, катящейся по другой окружности такой же, то след точки - кардиоида (сердце)

Другие кривые: трехлепестковая роза, цепная линия.

ВЫВОД: Кривая (линия) - есть след движущейся точки. Такой точкой в наших примерах является острие карандаша, острый край куска мела, раскаленный метеор, пронизывающий верхние слои атмосферы или ракета. Прямую линию тоже можно считать следом движущейся точки.

Рассмотреть свойства параболы и их применение в технике (фокусирование лучей, принцип действия параболической антенны)