Презентация к уроку математики "Призма"

Материал на украинском языке. Дана робота присвячена вивченню одного з розділів геометрії 11 класу. Містить необхідний теоретичний матеріал та підбір опорних задач, що дозволить учням глибше та доступніше сприйняти один з видів многогранників.

Призмою  називається многогранник, який складається з двох плоских многокутників, які лежать в різних площинах і суміщаються паралельним перенесенням, та всіх відрізків, що сполучають відповідні точки цих многокутників.

Многокутники називаються основами призми, а відрізки, які сполучають відповідні вершини,― бічними ребрами призми.

Оскільки паралельне перенесення є рух, то основи призми рівні.

Через те, що при паралельному перенесенні площина переходить у паралельну площину (або в себе), то основи призми лежать у паралельних площинах.

Оскільки при паралельному перенесені точки зміщуються вздовж паралельних прямих або прямих,які збігаються,на одну і ту саму відстань,то бічні ребра призми паралельні і рівні.

ПРИЗМА

Означення призми .

Елементи призми.

Види призм.

Призми вписані та описані.

Площа поверхні призми.

Об ‘єм призми .

Означення призми . Елементи призми

Призмою називається многогранник, який складається з двох плоских многокутників, які лежать в різних площинах і суміщаються паралельним перенесенням, та всіх відрізків, що сполучають відповідні точки цих многокутників.

Многокутники називаються основами призми , а відрізки, які сполучають відповідні вершини,― бічними ребрами призми .

• Оскільки паралельне перенесення є рух, то основи призми рівні .
• Через те, що при паралельному перенесенні площина переходить у паралельну площину (або в себе), то основи призми лежать у паралельних площинах .

Оскільки при паралельному перенесені точки зміщуються вздовж паралельних прямих або прямих,які збігаються,на одну і ту саму відстань,то бічні ребра призми паралельні і рівні .

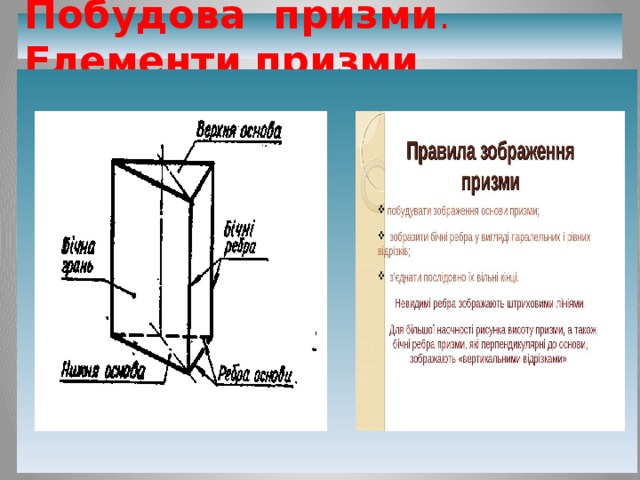
Побудова призми . Елементи призми

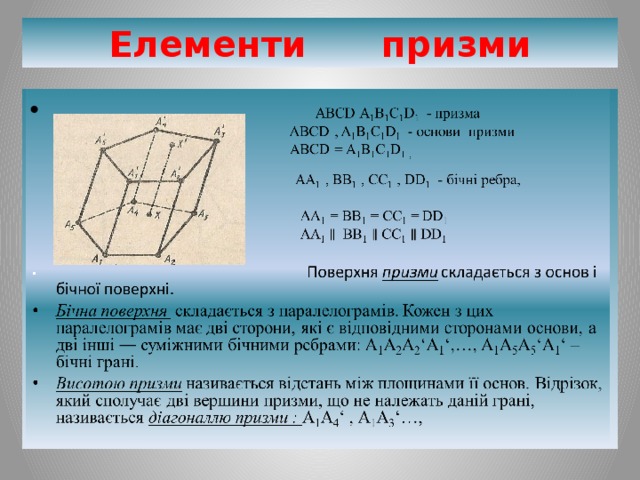
Елементи призми

ABCD A 1 B 1 C 1 D 1 - призма

ABCD , A 1 B 1 C 1 D 1 - основи призми

ABCD = A 1 B 1 C 1 D 1 ,

АА 1 , ВВ 1 , СС 1 , DD 1 - бічні ребра,

АА 1 = ВВ 1 = СС 1 = DD 1

АА 1 ВВ 1 СС 1 DD 1

• Поверхня призми складається з основ і бічної поверхні.

• Бічна поверхня складається з паралелограмів. Кожен з цих паралелограмів має дві сторони, які є відповідними сторонами основи, а дві інші ― суміжними бічними ребрами: А 1 А 2 А 2 ‘А 1 ‘,…, А 1 А 5 А 5 ‘А 1 ‘ – бічні грані.
• Висотою призми називається відстань між площинами її основ. Відрізок, який сполучає дві вершини призми, що не належать даній грані, називається діагоналлю призми : А 1 А 4 ‘ , А 1 А 3 ‘…,

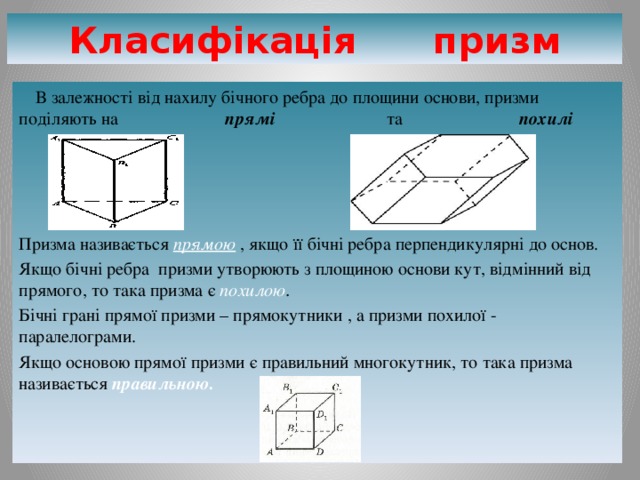
Класифікація призм

В залежності від нахилу бічного ребра до площини основи, призми поділяють на прямі та похилі

Призма називається прямою , якщо її бічні ребра перпендикулярні до основ.

Якщо бічні ребра призми утворюють з площиною основи кут, відмінний від прямого, то така призма є похилою .

Бічні грані прямої призми – прямокутники , а призми похилої - паралелограми.

Якщо основою прямої призми є правильний многокутник, то така призма називається правильною.

призми вписані та списані

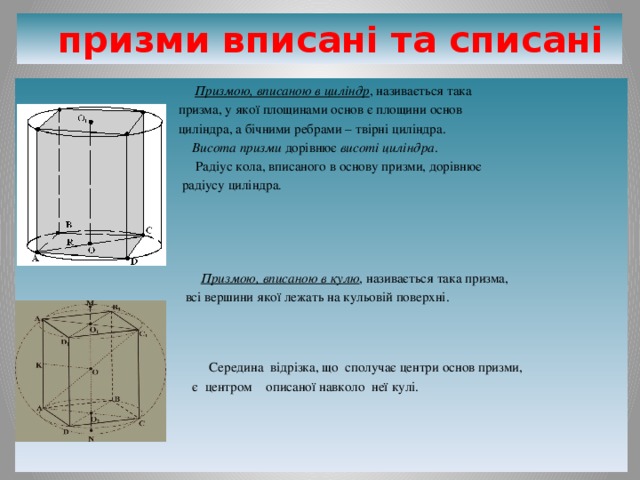
Призмою, вписаною в циліндр , називається така

призма, у якої площинами основ є площини основ

циліндра, а бічними ребрами – твірні циліндра.

Висота призми дорівнює висоті циліндра .

Радіус кола, вписаного в основу призми, дорівнює

радіусу циліндра .

Призмою, вписаною в кулю , називається така призма,

всі вершини якої лежать на кульовій поверхні.

Середина відрізка, що сполучає центри основ призми,

є центром описаної навколо неї кулі.

призми вписані та описані

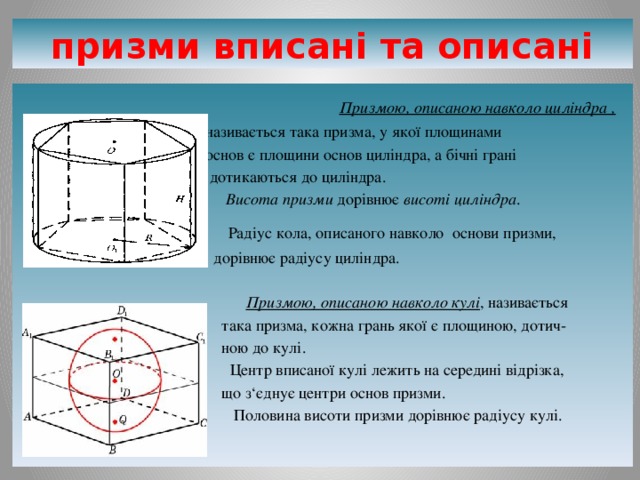
Призмою, описаною навколо циліндра ,

називається така призма, у якої площинами

основ є площини основ циліндра, а бічні грані

дотикаються до циліндра.

Висота призми дорівнює висоті циліндра .

Радіус кола, описаного навколо основи призми,

дорівнює радіусу циліндра.

Призмою, описаною навколо кулі , називається

така призма, кожна грань якої є площиною, дотич-

ною до кулі.

Центр вписаної кулі лежить на середині відрізка,

що з‘єднує центри основ призми.

Половина висоти призми дорівнює радіусу кулі.

Площа поверхні призми

Площа повної поверхні призми дорівнює сумі площ усіх її граней.

S поверхні = 2S основи + S бічне .

Теорема 1 .

Бічна поверхня прямої призми дорівнює добутку периметра основи на висоту призми, тобто на довжину бічного ребра.

Доведення: Бічні грані прямої призми ―прямокутники. Основи цих прямокутників є сторонами многокутника , що лежить в основі призми , а висоти дорівнюють довжині бічних ребер . Звідси випливає , що бічна поверхня призми дорівнює : S=a 1 l+a 2 l+…+a n l = pl, де а 1 …,а n ― довжини ребер основи, р ― периметр основи призми, а l― довжина бічних ребер. Теорему доведено.

Площа поверхні призми

Теорема 2 .

Площа бічної поверхні похилої призми дорівнює добутку периметра її перпендикулярного перерізу на довжину бічного ребра.

Доведення

Нехай у призмі А 1 А 2 …А n В 1 В 2 …В довжина бічного

ребра дорівнює l , перпендикулярний переріз

С 1 С 2 …С n має периметр Р. Треба довести, що S біч = ℓ•Р ┴ .

1) Перпендикулярний переріз призми проведений

перпендикулярно до якогось з її ребер , отже, площина

перерізу(за властивістю паралельних прямих)

перпендикулярна до всіх ребер даної призми. Тоді

відрізки С 1 С 2 , С 2 С 3 , …, С n С 1 є висотами паралелограмів

бічних граней.

2) Площа бічної поверхні призми дорівнює сумі площ паралелограмів її бічних граней:

Теорему доведено .

Об ‘єм призми

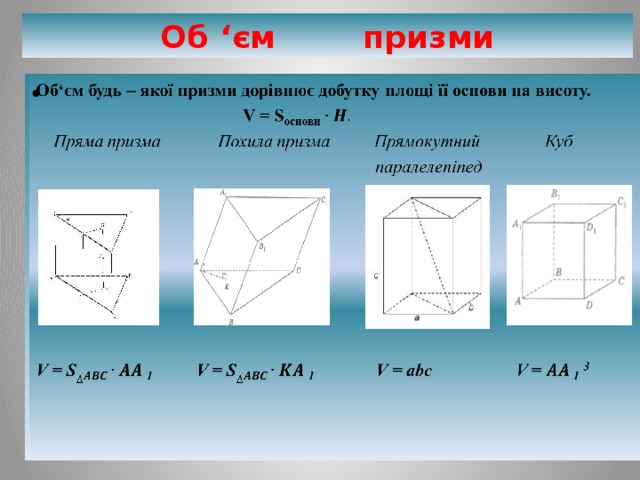
Об‘єм будь – якої призми дорівнює добутку площі її основи на висоту.

V = S основи

Пряма призма Похила призма Прямокутний Куб

паралелепіпед

V = S 1 V = S 1 V = abc V = 1 3

Виконаємо разом

Задача 1

Бічна поверхня правильної чотирикутної призми дорівнює 32 см 2 , а повна поверхня 40 см 2 . Знайти висоту призми.

Розв‘язання. Оскільки S поверхні = 2S основи + S бічне , то

2S основи = 40 – 32 = 8 (см 2 ),

S основи = 4 см 2 .

Основою правильної чотирикутної призми є квадрат, площа якого дорівнює 4 см 2 , тоді його сторона має довжину 2 см, отже периметр основи дорівнює 8 см.

Знаючи, що S бічне = p основи H,

H = = = 4 (см).

Відповідь: 4 см

Виконаємо разом

Задача 2

У прямому паралелепіпеді сторони основи 3 см і 8 см, кут між ними 60 °.

Бічна поверхня дорівнює 320 см 2 . Знайти повну поверхню призми.

Розв‘язання. S поверхні = 2S основи + S бічне .

Основою паралелепіпеда є паралелограм, площу якого обчислимо за формулою: S = a b sin (a, b)

S = 3 8 sin 60° = 12 (см 2 ),

S поверхні = 2 + 320 = 24 + 320 (см 2 ).

Відповідь: 24 + 320 см 2

Виконаємо разом

Задача 3

Три латунних куби з ребрами 3см, 4см і 5см переплавлено в один куб. Знайти ребро нового куба.

Розв‘язання. Об‘єм нового куба дорівнює сумі об‘ємів трьох кубів, тоді

V = + + = 27 + 64 + 125 = 216 (см 3 ),

отже а = = 6 (см)

Відповідь: 6см

Виконаємо разом

Задача 4

Знайти об‘єм прямокутного паралелепіпеда, діагональ якого a утворює з площиною основи кут , а з бічною гранню кут .

Розв‘язання.

Нехай на малюнку зображено прямокутний паралелепіпед, у якого діагональ B 1 D дорівнює а і утворює з площиною основи кут B 1 DB, що дорівнює , а з бічною гранню (DD 1 C 1 ) кут B 1 DC 1 , градусна міра якого .

Шуканий об‘єм знайдемо за формулою

V = abc = AB AD BB 1 .

За співвідношеннями між сторонами та кутами прямокутного трикутника B 1 DB, знайдемо невідомі катети :

BB 1 = a sin , BD = a cos .

Аналогічно, катет B 1 C 1 трикутника B 1 DC 1 дорівнює a sin .

Оскільки B 1 C 1 = AD , то з трикутника ABD визначимо за теоремою Піфагора катет AB:

AB = = = a . Отже, шуканий об‘єм дорівнює :

V = a a sin a sin = sin sin .

Відповідь : sin sin

Виконаємо разом

Задача 5

Знайти радіус кулі, описаної навколо куба із стороною а .

Розв‘язання.

Оскільки куб вписаний в кулю, то всі його вершини лежать на поверхні кулі.

Отже, діагональ куба є діаметром кулі.

АС 1 = а , де а – сторона куба,

тоді радіус кулі дорівнює

АС 1 = .

Відповідь :