Презентация к уроку математики "Линейные уравнения"

Основные понятия.

Равенство между двумя алгебраическими выражениями с одной переменной называют уравнением с одной неизвестной.

Корнем уравнения называют значение переменной, при котором уравнение обращается в верное числовое равенство. 

Решить уравнение означает найти все его корни или доказать, что корней нет.

Уравнения, которые имеют одни и те же корни, называются равносильными.

Определение линейного уравнения.

Уравнение вида aх = b (где х – переменная, а и b – некоторые числа) называется линейным уравнением с одной переменной.

Отличительная особенность такого уравнения – переменная х входит в уравнение обязательно в первой степени.

Распределите уравнения по группам.

Нелинейные.

Линейные.

Линейные уравнения

Презентацию подготовила учитель МОУ гимназии №9 Киренкина Вера Викторовна

Основные понятия

Равенство между двумя алгебраическими выражениями с одной

переменной называют уравнением с одной неизвестной

Корнем уравнения называют значение переменной , при котором уравнение обращается в верное числовое равенство.

Решить уравнение означает найти все его корни или доказать, что корней нет.

Уравнения, которые имеют одни и те же корни, называются равносильными .

Определение линейного уравнения

Уравнение вида a х = b (где х – переменная, а

и b – некоторые числа) называется линейным уравнением с одной переменной .

Отличительная особенность такого уравнения – переменная

х входит в уравнение обязательно в первой степени.

Распределите уравнения по группам

Линейные

Нелинейные

3х 2 +6х+7=0

2х 2 -5х 3 = 3

3 х=7

-2 х=5

х(х-3)=х 5

6х-10=х-3

Макрос создан программистом Хансом Хофманом (Германия)

Основные свойства

• Если в уравнении перенести

слагаемые из одной части в другую,

изменив его знак, то получится

уравнение, равносильное данному;

• Если обе части уравнения умножить или разделить на одно и то же отличное от нуля число, то получится уравнение равносильное данному.

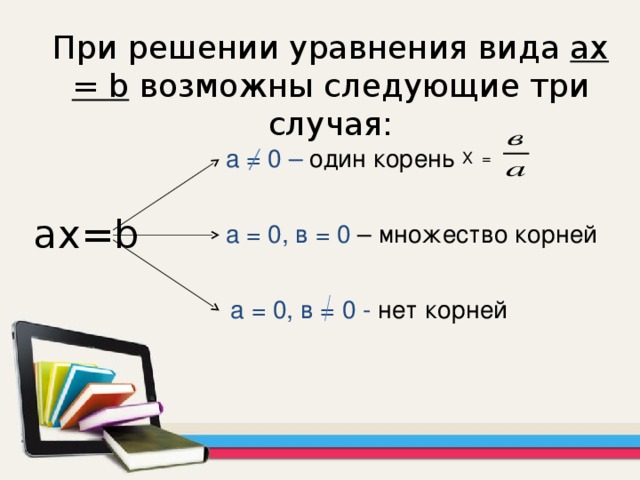
При решении уравнения вида ах = b возможны следующие три случая:

ах= b

а = 0 – один корень

Х =

а = 0, в = 0 – множество корней

а = 0, в = 0 - нет корней

Пример 1

Решим уравнение:

Раскроем скобки:

Получим выражение:

Слагаемые, зависящие от х, перенесём в левую часть уравнения; числа – в правую, изменяя их знаки на противоположные:

Приведем подобные:

Найдем неизвестный множитель:

Получаем решение:

Пример 2

Решим уравнение:

Раскроем скобки:

Получим выражение:

Слагаемые, зависящие от х, перенесём в левую часть уравнения; числа – в правую, изменяя их знаки на противоположные:

Приведем подобные:

При подстановке любого значения х

получаем верное числовое равенство 0=0

Получаем решение:

Пример 3

Решим уравнение:

Раскроем скобки:

Получим выражение:

Слагаемые, зависящие от х, перенесём в левую часть уравнения; числа – в правую, изменяя их знаки на противоположные:

Приведем подобные:

При подстановке любого значения x

Получаем решение:

получаем неверное числовое равенство 0=14

Реши самостоятельно

1. 2.

Ответ:

Ответ:

-3

Спасибо за внимание