Презентация к проекту по математике "Симметрия вокруг нас"

Цель проекта:

Задачи проекта:

Изучить учебную и научную литературу по данной  теме;

Найти симметричные  фигуры  и  предметы в  окружающем  мире;

Методом  измерения  исследовать  наличие  симметрии  в  собственном  окружении.

Определить значение использования симметрии;

Расширить  математический  кругозор.

Этамы работы:

Ознакомление с предметом  исследования на уроках математики. Миниисследования;

Изучение  дополнительных  информационных  источников;

Проведение  исследования при помощи измерений в окружающей меня обстановке;

Работа над презентацией;

Изготовление буклета «Симметрия в архитектуре г. Рязани и с. Захарово».

В древности слово симметрия употреблялось в значении «гармония» и «красота».

Симметрия - От греч. symmetria – «соразмерность, пропорциональность, одинаковость в расположении частей».

В геометрии симметрия - это свойство геометрических фигур при отображении плоскости и пространства. Виды симметрии: центральная, осевая, зеркальная, винтовая, поворотная, переносная.

Закон симметрии

Ещё в XIX веке исследования в этой области привели к заключению, что симметрия природных форм в значительной степени зависит от влияния сил земного тяготения, которое в каждой точке имеет симметрию конуса. В результате был найден следующий закон, которому подчиняются формы природных тел:

Всё, что растёт или движется по вертикали, то есть вверх или вниз относительно земной поверхности, подчиняется радиально-лучевой симметрии. Всё то, что растёт и движется горизонтально или наклонно по отношению к земной поверхности, подчиняется билатеральной (зеркальной)симметрии.

Давайте представим, что всё в природе асимметрично. Это что же получится? Всё будет некрасивым.

«…быть прекрасным, значит быть соразмерным» (Платон).

Выводы

Практически все живые существа на планете  симметричны.  Большинство  видов  обладает  осевой и зеркальной симметрией,  некоторые  подводные  обитатели  обладают  центральной  симметрией.

В любом растении можно найти какую-то его часть, обладающую  осевой,  центральной, поворотной или винтовой симметрией. Это  могут  быть  листья,  цветы, стебли, стволы деревьев, плоды  и  более мелкие  части.

Симметрия форм, окраски  насекомых,  животных, растений  придает им красоту.

Симметрия является одним из принципов гармонического построения мира. «Сфера влияния» симметрии поистине безгранична. Всюду она определяет гармонию природы, мудрость науки и красоту.

 Действительно, симметрию мы можем наблюдать везде. Она    противостоит хаосу, беспорядку. Значит, симметрия –

- гармония и красота,

- равновесие,

- устойчивость.

Симметрия вокруг нас

Выполнила:

Ученица 8б класса

ЗСОШ №1

Борисова Елена.

Руководитель:

Учитель математики

Полякова Татьяна Васильевна.

• О, Симметрия! Гимн тебе пою! Тебя повсюду в мире узнаю. Ты в Эйфелевой башне, в малой мошке, Ты в елочке, что у лесной дорожки. С тобою дружен и тюльпан, и роза, И снежный рой – творение мороза! (Автор неизвестен)

Цель проекта:

• Изучение многообразия симметрии , поиск и исследование симметрии в мире растений, животных, неживой природе

Задачи проекта:

• Изучить учебную и научную литературу по данной теме;
• Найти симметричные фигуры и предметы в окружающем мире;
• Методом измерения исследовать наличие симметрии в собственном окружении.
• Определить значение использования симметрии;
• Расширить математический кругозор.

Этапы работы

• Ознакомление с предметом исследования на уроках математики. Миниисследования;
• Изучение дополнительных информационных источников;
• Проведение исследования при помощи измерений в окружающей меня обстановке;
• Работа над презентацией;
• Изготовление буклета «Симметрия в архитектуре г. Рязани и с. Захарово»

В древности слово симметрия употреблялось в значении «гармония» и «красота» Симметрия - От греч. symmetria – «соразмерность, пропорциональность, одинаковость в расположении частей»

• В геометрии симметрия - это свойство геометрических фигур при отображении плоскости и пространства.
• Виды симметрии: центральная, осевая, зеркальная, винтовая, поворотная, переносная.

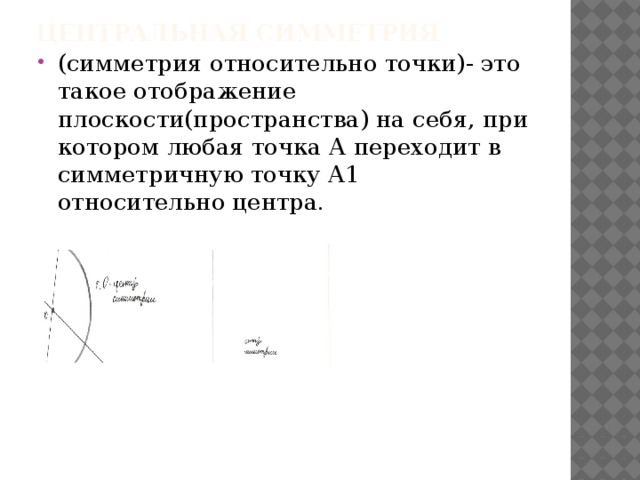
Центральная симметрия

• (симметрия относительно точки)- это такое отображение плоскости(пространства) на себя, при котором любая точка А переходит в симметричную точку А1 относительно центра.

Осевая симметрия

• (симметрия относительно прямой) - это такое отображение плоскости(пространства) на себя, при котором любая точка А переходит в симметричную точку А1 относительно прямой.

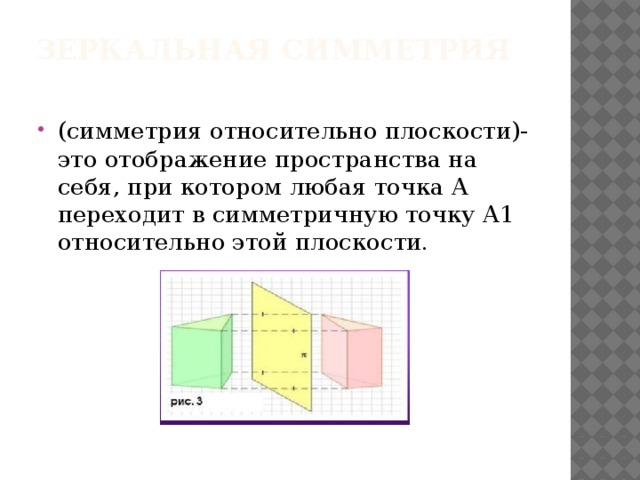
Зеркальная симметрия

• (симметрия относительно плоскости)- это отображение пространства на себя, при котором любая точка А переходит в симметричную точку А1 относительно этой плоскости.

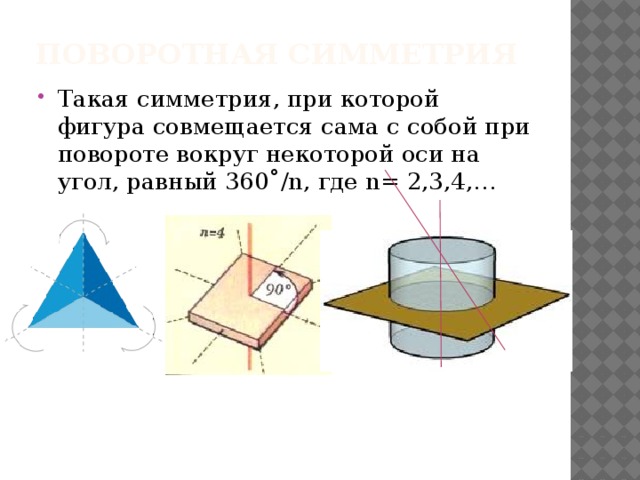
Поворотная симметрия

• Такая симметрия, при которой фигура совмещается сама с собой при повороте вокруг некоторой оси на угол, равный 360˚/n, где n= 2,3,4,…

Винтовая симметрия

• Симметрия относительно группы преобразований: преобразование поворота вокруг оси и переноса его вдоль этой оси.

Переносная симметрия

• (трансляционная). При переносе вдоль прямой АB на расстояние, равное а, фигура совмещается сама с собой. Прямая, вдоль которой происходит перемещение объекта, называется осью переноса, расстояние а- периодом.

а

Земля в представлении большинства начитанных людей до эпохи Коперника была центром мироздания. Поэтому прямые, проходящие через центр Земли, они считали центром Вселенной. Поэтому даже макет Земли - глобус имеет ось симметрии.

Симметрия в мире растений

• Центральная симметрия (лучевая= лучистая, радиальная)
• Фигура симметрична относительно точки (центр О), если её точки попарно лежат на прямых, проходящих через центр О, по разные стороны и на равных расстояниях от него .
• Форма симметрии, при которой тело (или фигура) совпадает само с собой при вращении объекта вокруг определённой точки .

В

А

• Ею обладают в основном цветки растений.

Поворотная симметрия.

80˚

Осевая симметрия

Ярко выраженной осевой симметрией обладают листья, ветви, цветы, плоды.

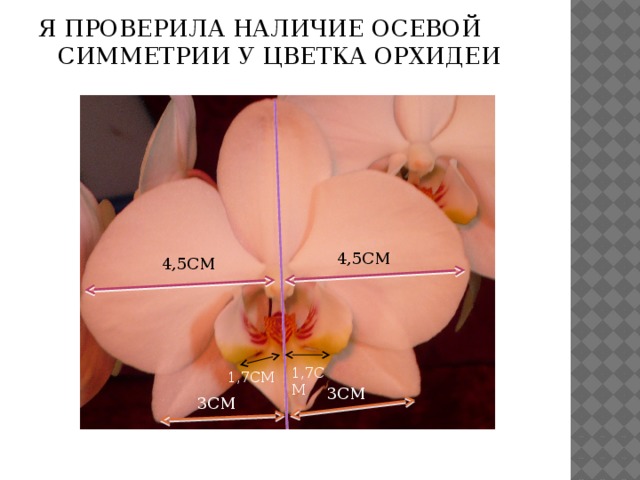
Я ПРОВЕРИЛА НАЛИЧИЕ ОСЕВОЙ СИММЕТРИИ У ЦВЕТКА ОРХИДЕИ

4,5СМ

4,5СМ

1,7СМ

1,7СМ

3СМ

3СМ

• Осевая симметрия у филодендрона и финика пальчатого

9

9

14

14

3

3

2

2

• Для деревьев характерна симметрия конуса, которая хорошо видна на примере фактически любого дерева. Ствол - ось симметрии.

Винтовая симметрия ярко проявляется в расположении листьев на стебле, веток на стволе, в строении шишек. Стебель обладает винтовой осью симметрии . У подсолнечника каждый листок появляется после поворота на 72˚. Располагаясь винтом по стеблю, листья как бы раскидываются в разные стороны и не заслоняют друг друга от света, хотя сами листья тоже имеют ось симметрии.

6,1

Я ИССЛЕДОВАЛА ВЕТОЧКУ ФИКУСА, РАСТУЩЕГО В МОЕМ ДОМЕ, ОКАЗАЛОСЬ, ЧТО ОНА ТОЖЕ ОБЛАДАЕТ ВИНТОВОЙ СИММЕТРИЕЙ, ПРИЧЁМ РАССТОЯНИЕ МЕЖДУ ЛИСТЬЯМИ,РАСПОЛОЖЕННЫМИ НА ОДНОЙ СТОРОНЕ СТЕБЛЯ И ЛИСТЬЯМИ НА ДРУГОЙ СТОРОНЕ СТЕБЛЯ,В МОЕМ СЛУЧАЕ ОКАЗАЛИСЬ ПРИБЛИЖЕННО РАВНЫ 6,1 СМ, А ВСЕ ЛИСТОЧКИ НАКЛОНЕНЫ К СТЕБЛЮ ПОД УГЛОМ 65˚

65˚

6,1

Зеркальная симметрия

С горизонтальной зеркальной симметрией мы встречаемся редко. Ее нашла совершенно случайно. Мне просто понравился пейзаж и я его решила сфотографировать. Оказывается, отражение в воде – единственный пример горизонтальной симметрии в природе.

3,1

3,1

Симметрия в животном мире.

• Под симметрией у животных понимают соответствие в размерах и форме, а также расположение частей тела, находящихся на противоположных сторонах разделяющей линии (плоскости симметрии).

Зеркальная симметрия

Я проверила наличие зеркальной симметрии у бабочки и майского жука. Если проведём вертикальную линию на тельце бабочки, жука, в морде собаки, коровы , кота, например, видна зеркальная симметрия. 

ммм

Я нашла симметрию и у своего кота

Значение Билатеральной симметрии.

Мы не разу не видели, чтобы у любого насекомого лапы слева были бы больше, чем справа, а правое крыло бабочки или божьей коровки было бы больше, чем левое. Такого в природе не бывает, иначе насекомые не смогли бы летать.

Значение зеркальной симметрии.

Органы, управляющие движением, вся нервная система, включая спинной и головной мозг животных и человека, имеют двустороннюю симметрию. При таком устройстве мозга значительно проще организовать слаженную работу плавников, ног или крыльев, чтобы активно перемещаться в пространстве, избегая столкновения с подвижными и неподвижными предметами, неукоснительно поддерживать равновесие тела, осуществлять безаварийное приземление в заданной точке пространства и совершать другие координированные движения.

• Снежинки – самый яркий пример красоты форм осевой симметрии. Она таит в себе все виды симметрии: центральную,поворотную, осевую и каждая снежинка зеркально симметрична.

• Законы симметрии в равной мере распространяются и на творение рук человеческих. Одним из самых наглядных использований законов симметрии жизни служит строения архитектуры.

Закон симметрии

Ещё в XIX веке исследования в этой области привели к заключению, что симметрия природных форм в значительной степени зависит от влияния сил земного тяготения, которое в каждой точке имеет симметрию конуса. В результате был найден следующий закон, которому подчиняются формы природных тел:

Всё, что растёт или движется по вертикали, то есть вверх или вниз относительно земной поверхности, подчиняется радиально-лучевой симметрии. Всё то, что растёт и движется горизонтально или наклонно по отношению к земной поверхности, подчиняется билатеральной (зеркальной)симметрии.

• Давайте представим, что всё в природе асимметрично. Это что же получится? Всё будет некрасивым:

«…быть прекрасным,

значит быть

соразмерным»

(Платон).

Выводы

• Практически все живые существа на планете симметричны. Большинство видов обладает осевой и зеркальной симметрией, некоторые подводные обитатели обладают центральной симметрией.
• В любом растении можно найти какую-то его часть, обладающую осевой, центральной, поворотной или винтовой симметрией. Это могут быть листья, цветы, стебли, стволы деревьев, плоды и более мелкие части.
• Симметрия форм, окраски насекомых, животных, растений придает им красоту.
• Симметрия   является одним из принципов гармонического построения мира. «Сфера влияния» симметрии поистине безгранична. Всюду она определяет гармонию природы, мудрость науки и красоту.
• Действительно, симметрию мы можем наблюдать везде. Она противостоит хаосу, беспорядку. Значит, симметрия –
• -гармония и красота,
• -равновесие,
• -устойчивость.