Презентация для подготовки к ЕГЭ по математике

Тип задания. Стереометрическая задача на нахождение геометрических величин (длин, углов, площадей объёмов).

Характеристика задания. Несложное задание по стереометрии на применение основных формул, связанных с вычислением площадей поверхностей или объёмов многогранников (пирамид и призм) или тел вращения (цилиндров, конусов, шаров), в том числе вписанных или описанных около других многогранников или тел вращения.

Комментарий. Для решения задачи достаточно знать формулы площадей поверхностей и объёмов пирамиды, призмы, цилиндра, конуса и шара.

Типичные ошибки:

перепутать площадь поверхности с объемом;

при изменении радиуса некоторых тел в несколько раз, объем меняем ошибочно в это же количество раз, но надо смотреть на формулу, радиус может быть в квадрате (а значит надо изменять объем дважды в это количество раз) или в кубе (значит надо изменять объем трижды в это количество раз).

Полную информацию смотрите в файле. 

Задания В11

ЕГЭ по математике

Автор: учитель математики

МКОУ «Безголосовская СОШ»

Николайцева Лариса Николаевна

• Тип задания. Стереометрическая задача на нахождение геометрических величин (длин, углов, площадей объёмов).

• Характеристика задания. Несложное задание по стереометрии на применение основных формул, связанных с вычислением площадей поверхностей или объёмов многогранников (пирамид и призм) или тел вращения (цилиндров, конусов, шаров), в том числе вписанных или описанных около других многогранников или тел вращения.

• Комментарий . Для решения задачи достаточно знать формулы площадей поверхностей и объёмов пирамиды, призмы, цилиндра, конуса и шара.

Типичные ошибки:

• перепутать площадь поверхности с объемом;
• при изменении радиуса некоторых тел в несколько раз, объем меняем ошибочно в это же количество раз, но надо смотреть на формулу, радиус может быть в квадрате (а значит надо изменять объем дважды в это количество раз) или в кубе (значит надо изменять объем трижды в это количество раз).

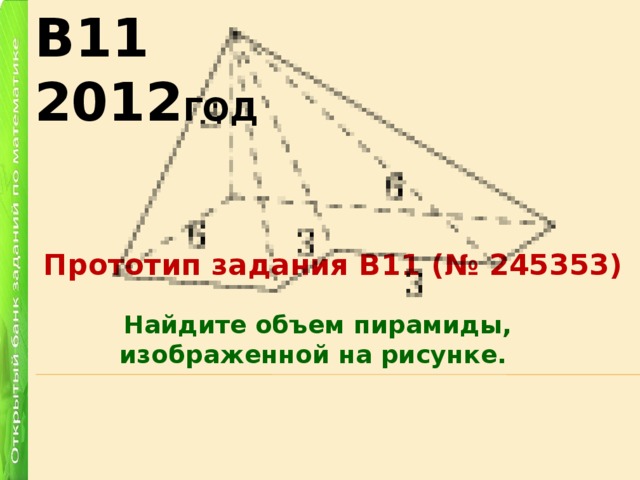
В11 2012 год

Прототип задания B11 (№ 245353)

Найдите объем пирамиды, изображенной на рисунке.

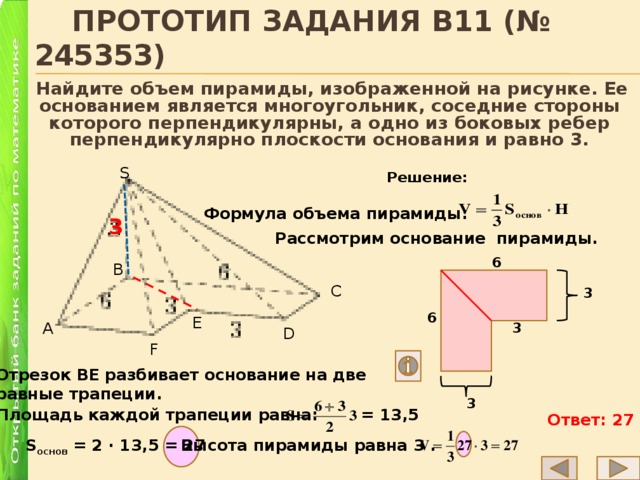
Прототип задания B11 (№ 245353)

Найдите объем пирамиды, изображенной на рисунке. Ее основанием является многоугольник, соседние стороны которого перпендикулярны, а одно из боковых ребер перпендикулярно плоскости основания и равно 3.

S

Решение:

Формула объема пирамиды:

3

Рассмотрим основание пирамиды.

6

B

C

3

6

E

A

3

D

F

Отрезок ВЕ разбивает основание на две

равные трапеции.

3

Площадь каждой трапеции равна:

= 13,5

Ответ: 27

Высота пирамиды равна 3 .

S основ = 2 ∙ 13,5 = 27

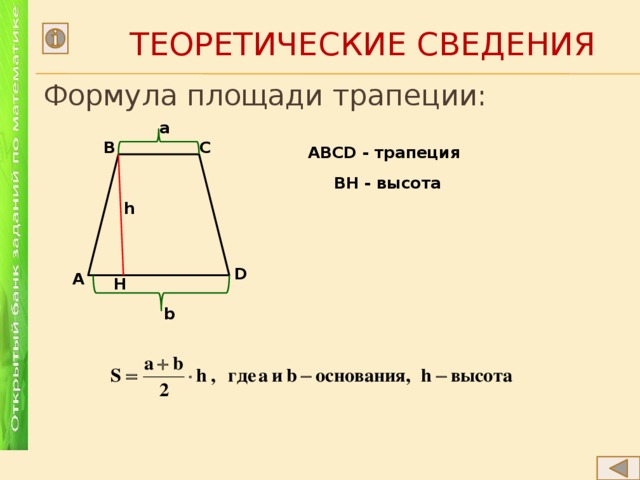
Теоретические сведения

• Формула площади трапеции:

a

С

В

ABCD - трапеция

ВН - высота

h

D

А

H

b

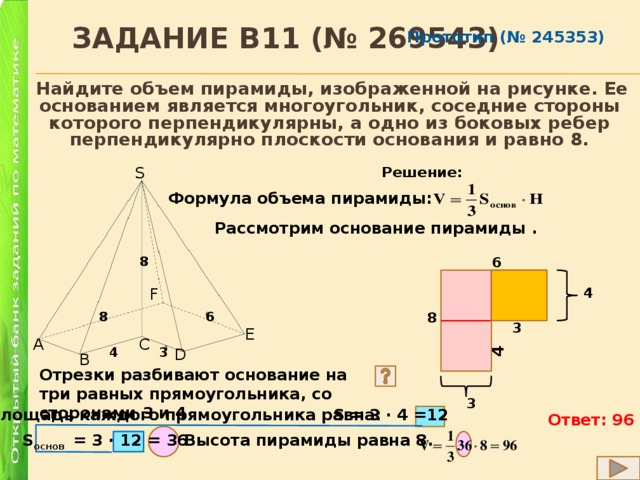
Задание B11 (№ 269543)

4

Прототип (№ 245353)

Найдите объем пирамиды, изображенной на рисунке. Ее основанием является многоугольник, соседние стороны которого перпендикулярны, а одно из боковых ребер перпендикулярно плоскости основания и равно 8.

S

Решение:

Формула объема пирамиды:

Рассмотрим основание пирамиды .

8

6

F

4

8

8

6

3

E

A

C

4

3

D

B

Отрезки разбивают основание на три равных прямоугольника, со сторонами 3 и 4

3

S = 3 ∙ 4 =12

Площадь каждого прямоугольника равна:

Ответ: 96

Высота пирамиды равна 8.

S основ = 3 ∙ 12 = 36

Теоретические сведения

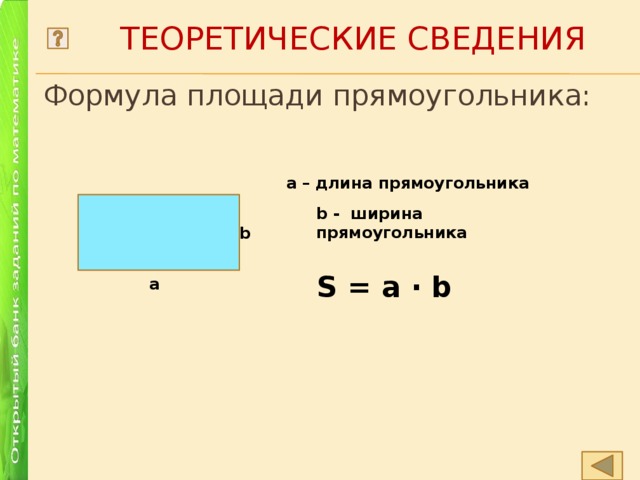
• Формула площади прямоугольника:

a – длина прямоугольника

b - ширина прямоугольника

b

S = a ∙ b

a

Задание B11 (№ 270037)

Прототип (№ 245353)

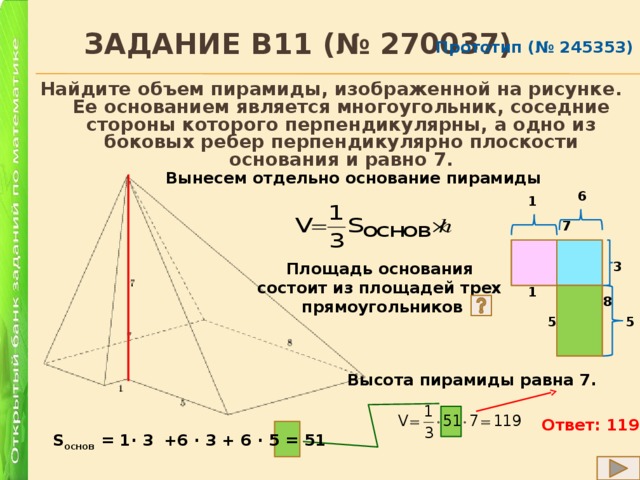
Найдите объем пирамиды, изображенной на рисунке. Ее основанием является многоугольник, соседние стороны которого перпендикулярны, а одно из боковых ребер перпендикулярно плоскости основания и равно 7.

Вынесем отдельно основание пирамиды

6

1

7

Площадь основания

3

состоит из площадей трех

прямоугольников

1

8

5

5

Высота пирамиды равна 7.

Ответ: 119

S основ = 1∙ 3 +6 ∙ 3 + 6 ∙ 5 = 51

Диагн. Раб. 25.01.12

В11 Дана правильная треугольная призма ABCA 1 B 1 C 1 , площадь основания которой равна 6, а боковое ребро равно 8. Найдите объем многогранника, вершинами которого являются точки ABCA 1 C 1 ,

A 1

С 1

В 1

С

A

В

Трен. раб.27.09.11

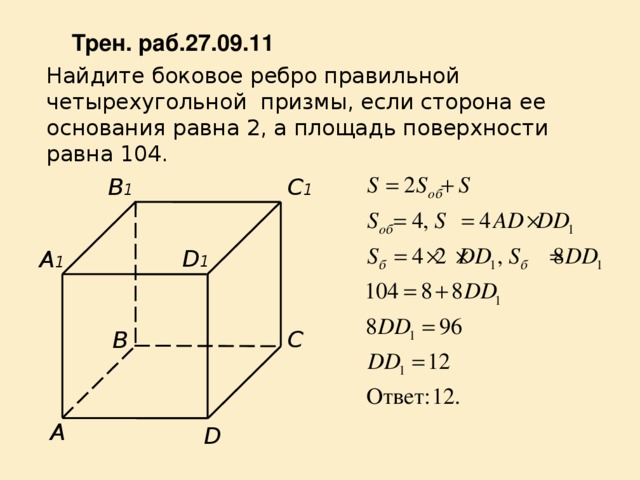
Найдите боковое ребро правильной четырехугольной призмы, если сторона ее основания равна 2, а площадь поверхности равна 104.

B 1

C 1

D 1

А 1

C

B

А

D

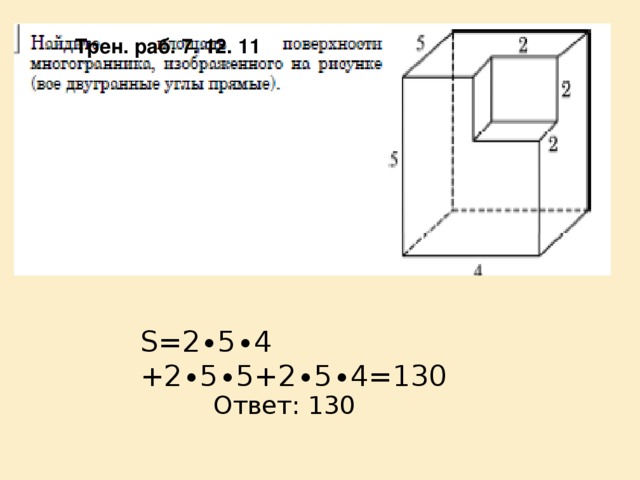
Трен. раб. 7. 12. 11

S=2∙5∙4 +2∙5∙5+2∙5∙4=130

Ответ: 130

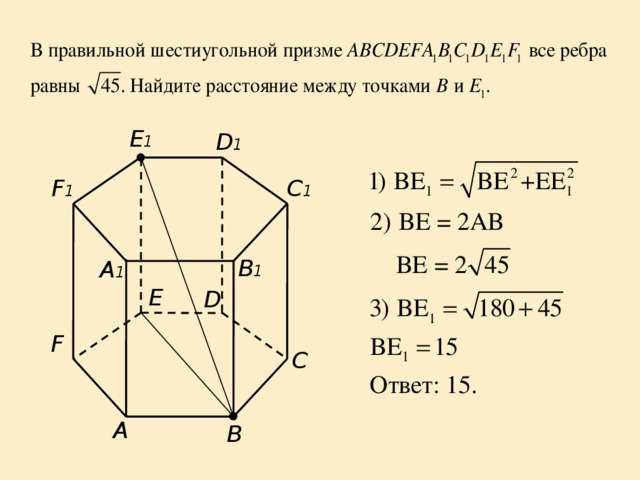
E 1

D 1

F 1

C 1

B 1

A 1

E

D

F

C

A

B

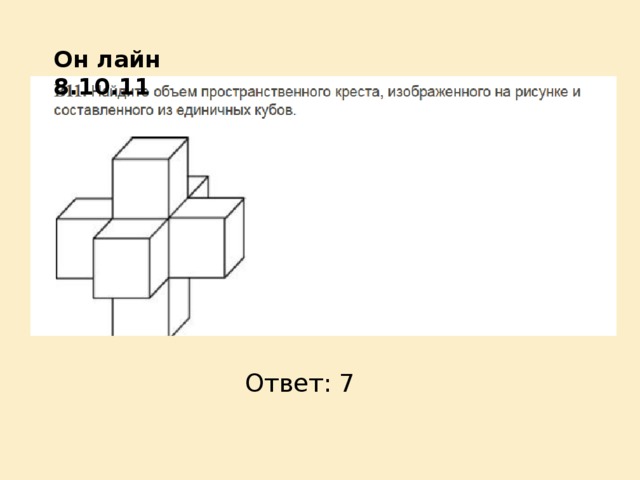
Он лайн 8.10.11

Ответ: 7

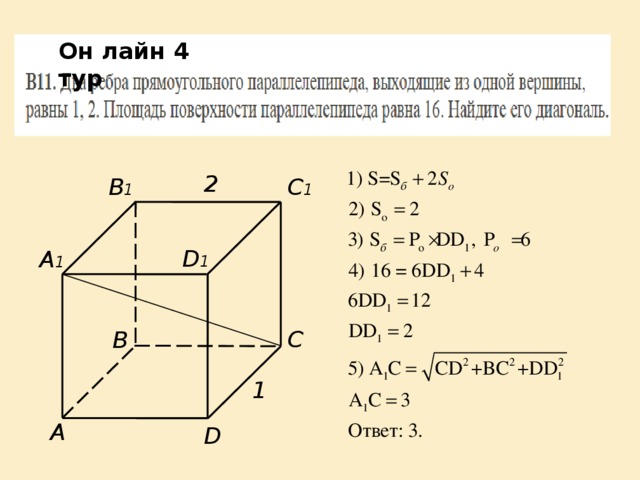
Он лайн 4 тур

2

C 1

B 1

D 1

А 1

C

B

1

А

D

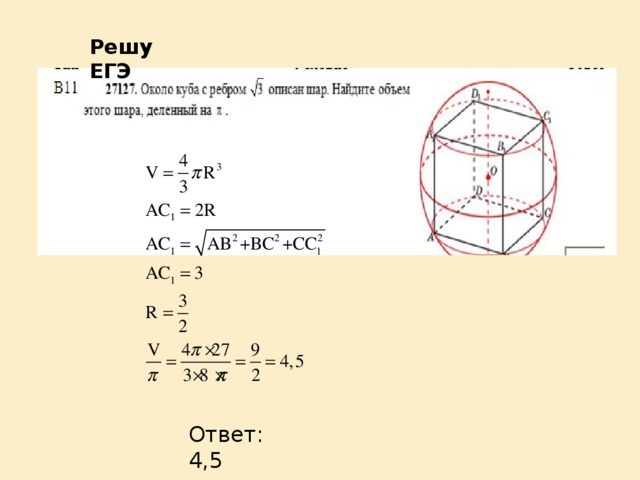
Решу ЕГЭ

Ответ: 4,5

Демо, 2012

Ответ: 9

Ященко

Ответ: 2175