Правильные многогранники вокруг нас

ЦЕЛЬ:

Рассмотреть вопросы практического применения многогранников в жизни человека.

Ознакомится с видами многогранников и их свойствами.

Рассмотреть современные гипотезы обустройства мира.

Изучить связь многогранников с живой природой.

Рассмотреть практическое применение многогранников.

Вопрос: Сможет ли человек в наше время жить без многогранников?

Древнегреческий ученый и философ Платон считал, что эти тела олицетворяют сущность природы.

Поэтому эти многогранники называют Платоновыми телами.

Пифагорейцы  уделяли в своих космологических теориях особенно важное место правильным многогранникам, неоценимое превосходство которых над всеми другими телами они усмотрели в том, что их только пять.  

Правильные многогранники вокруг нас

Выполнила:

Учитель математики

МБОУ СОШ №1

С. АЛЕКСАНДРОВ ГАЙ

САРАТОВСКАЯ ОБЛАСТЬ

Касимова Лидия Владимировна

ЦЕЛЬ: Рассмотреть вопросы практического применения многогранников в жизни человека.

• Ознакомится с видами многогранников и их свойствами.
• Рассмотреть современные гипотезы обустройства мира.
• Изучить связь многогранников с живой природой.
• Рассмотреть практическое применение многогранников.
• Вопрос : Сможет ли человек в наше время жить без многогранников ?

В своих философских теориях правильные многогранники использовали:

Кеплер

Платон

Евклид

Пифагор

Архимед

Древнегреческий ученый и философ Платон считал, что эти тела олицетворяют сущность природы.

Поэтому эти многогранники называют Платоновыми телами.

Пифагорейцы уделяли в своих космологических теориях особенно важное место правильным многогранникам, неоценимое превосходство которых над всеми другими телами они усмотрели в том, что их только пять .

Правильными многогранниками занимался Архимед. Ему также принадлежит открытие тринадцати так называемых полуправильных многогранников («архимедовых тел»).

Учение о правильных многогранниках, содержащееся в последней XIII книге Евклида, является венцом его «Начал».

Признаки правильных многогранников

Многогранник – выпуклый

Все его грани – равные правильные многоугольники

В каждой вершине сходится одинаковое число граней

Равны все двугранные углы, содержащие две грани с общим ребром.

Тетраэдр

Составлен из 4 равносторонних треугольников. Каждая его вершина является вершиной трёх треугольников. Следовательно: сумма плоских углов при каждой вершине равна 180°.

Гексаэдр или куб

Составлен из 6 квадратов. Каждая вершина куба является вершиной трёх квадратов. Следовательно: сумма плоских углов при каждой вершине равна 270º.

Октаэдр

Составлен из 8 равносторонних треугольников.

Каждая вершина октаэдра является вершиной четырёх треугольников.

Следовательно:

сумма плоских углов при каждой вершине 240º.

Икосаэдр

Составлен из 20 равносторонних треугольников. Каждая вершина икосаэдра является вершиной пяти треугольников. Следовательно:

сумма плоских углов при каждой вершине равна 300º .

Додекаэдр

Составлен из 12 правильных пятиугольников. Каждая вершина додекаэдра является вершиной трёх правильных пятиугольников. Следовательно:

сумма плоских углов при каждой вершине равна 324º .

Правильные многогранники

Правильный многогранник

Число

Граней

Тетраэдр

4

Вершин

Куб

Ребер

6

4

Октаэдр

6

Додекаэдр

8

8

12

12

Икосаэдр

6

20

20

12

30

12

30

Формула Эйлера .

Эйлерова характеристика всякого многогранника нулевого рода равна 2. Иначе говоря, между Г , В и Р любого многогранника нулевого рода имеет место зависимость .

В + Г – Р = 2

В – число вершин, Г – число граней, .Р – число ребер

Гипотеза Кеплер предположил, что расстояния между шестью известными тогда планетами выражаются через размеры пяти правильных выпуклых многогранников .

• Вокруг сферы Меркурия, ближайшей к Солнцу планеты, описан октаэдр
• Этот октаэдр вписан в сферу Венеры, вокруг которой описан икосаэдр .
• Вокруг икосаэдра описана сфера Земли, а вокруг этой сферы - додекаэдр .
• Додекаэдр вписан в сферу Марса, вокруг которой описан тетраэдр
• Вокруг тетраэдра описана сфера Юпитера, вписанная в куб .
• Наконец, вокруг куба описана сфера Сатурна.

Современные гипотезы обустройства мира

• Идеи Пифагора, Платона, Кеплера о связи правильных многоугольников с гармоничным устройством мира и в наше время нашли свое продолжение в интересной научной гипотезе, которую высказали в начале 80-х гг. ХХ века московские инженеры В.Макаров и В. Морозов.
• Они считают, что ядро Земли имеет форму и свойства растущего кристалла, оказывающего воздействие на развитие всех природных процессов, идущих на планете. Лучи этого кристалла, а точнее его силовое поле, обусловливают икосаэдро-додекаэдровую структуру Земли. Она проявляется в том, что в земной коре как бы проступают проекции вписанных в земной шар правильных многогранников: икосаэдра и додекаэдра. Многие залежи полезных ископаемых тянутся вдоль икосаэдро-додекаэдровой сетки; 62 вершины и середины ребер многогранников, называемых авторами узлами, обладают рядом специфических свойств, позволяющих объяснить некоторые непонятные явления. Здесь располагаются очаги древнейших культур и цивилизаций: Перу, Северная Монголия, Гаити, Обская культура и другие. В этих точках наблюдаются максимумы и минимумы атмосферного давления, гигантские завихрения мирового океана. В этих узлах находится озеро Лох-Несс, Бермудский треугольник. Дальнейшие исследования Земли, возможно, определят отношение к этой научной гипотезе, в которой, как видно, правильные многогранники занимают важное место.

Пять элементов

• Начиная с 7 века до нашей эры в Древней Греции создаются философские школы , в которых происходит постепенный переход от практической к философской геометрии.  Большое значение в этих  школах приобретают рассуждения, с  помощью которых удалось получать новые геометрические свойства.
• Существование пяти правильных многогранников относили к строению материи и Вселенной. Пифагорейцы, а затем Платон полагали, что материя состоит из четырех  основных элементов:  огня, земли, воздуха и воды.
• А так как пятой стихии в природе не было, то по их учению додекаэдр представлял собой всю Вселенную, то есть они считали, что мы живём внутри небесного свода, имеющего форму поверхности правильного додекаэдра.

о г о н ь

В О Д А

ВОЗДУХ

ЗЕМЛЯ

В С Е ЛЕН Н А Я

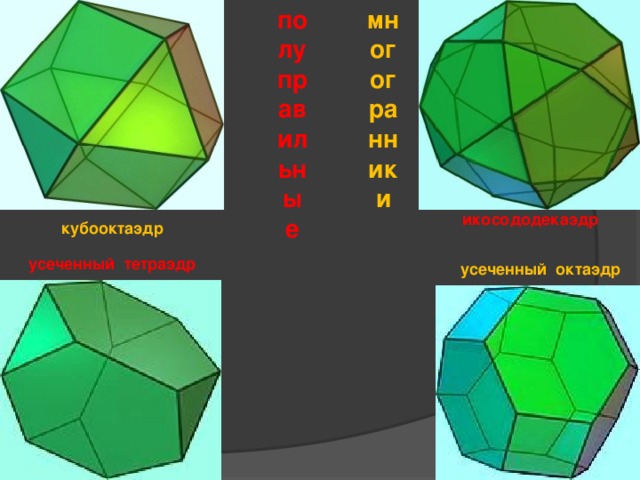
полуправильные

многогранники

икосододекаэдр

кубооктаэдр

усеченный тетраэдр

усеченный октаэдр

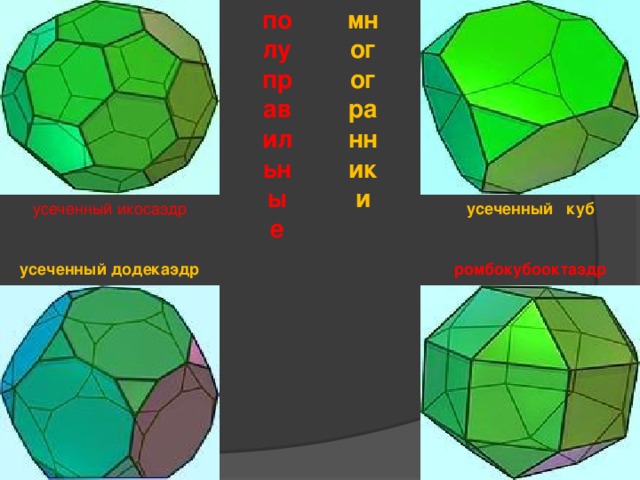
полуправильные

многогранники

усеченный икосаэдр

усеченный куб

усеченный додекаэдр

ромбокубооктаэдр

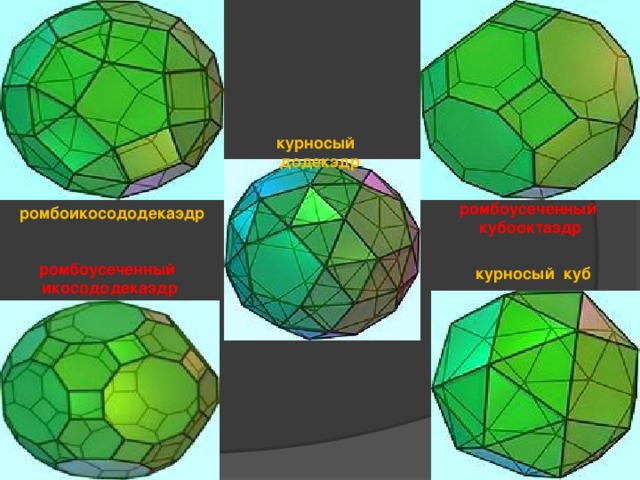
курносый додекэдр

ромбоусеченный кубооктаэдр

ромбоикосододекаэдр

ромбоусеченный икосододекаэдр

курносый куб

Многогранники в архитектуре

Музей Плодов в Яманаши Ицуко Хасегава

Великая пирамида в Гизе

Александрийский маяк

Фаросский маяк

Один из Японских музеев

Многогранники в родном крае

Остров Буян

Мечеть

здание Администрации

Многогранники в природе

• Правильные многогранники – самые выгодные фигуры.

• Удивительно разнообразен мир кристаллов, являющихся природными многогранниками.

• Подтверждением тому служит форма некоторых кристаллов (поваренная соль, сернистый колчедан).

• Но кроме формы правильных многогранников, многие кристаллы имеют форму просто многогранника (кварц, исландский шпат, пирит, гранат, алмаз)!

Кристалл поваренной соли

Кристаллическая решетка поваренной соли имеет кубическую структуру.

Кристаллы в форме октаэдра

Квасцы

Шпинель

Флюорит

Алмаз

Кристаллы в форме призм

Рубин

Горный хрусталь

Простейшее

• Скелет одноклеточного организма феодарии (Circogonia icosahedra) по форме напоминает икосаэдр.
• Большинство феодарий живут на морской глубине и служат добычей коралловых рыбок. Но простейшее животное защищает себя двенадцатью иглами, выходящими из 12 вершин скелета. Он больше похоже на звёздчатый многогранник.

Из всех многогранников с тем же числом граней икосаэдр имеет наибольший объём при наименьшей площади поверхности.

Это свойство помогает морскому организму преодолевать давление толщи воды.

Вирусы-бактериофаги

Головка вируса-бактериофага также имеет форму икосаэдра

Вывод :

Изучив работы великих математиков, я пришла к выводу, что этот вопрос полностью на современном этапе не изучен.

Поставленная цель была достигнута, задачи выполнены. Для себя я сделала вывод, что многогранники окружают нас. И мы живем среди них, любуясь их красотой и совершенством.

Источники информации

• http://images.yandex.ru/ - картинки для презентации искались с помощью этой поисковой системы
• http://ru.wikipedia.org/ -источник информации о многогранниках