Презентация к исследовательской работе по математике "Многогранники в ювелирном деле"

Цель работы:

Исследовать, как геометрические фигуры, в частности: многогранники, используются в ювелирном деле.

Задачи:

Ознакомиться с многогранниками, их видами. Дать понятие правильных многогранников.

Показать связь геометрии и драгоценных камней.

Гипотеза:

Заключается в том, что наш мир не может существовать без многогранников, и их роль важна.

Актуальность темы:

Современного человека вообще тяжело представить без драгоценностей. Сейчас достаточно мастерских по изготовлению и ремонту эксклюзивных изделий из драгметаллов, где каждый клиент сможет подобрать для себя необходимую услугу.

Как во многих сферах человеческой деятельности, так и ювелирном искусстве существуют свои модные течение. Но все же проходят десятилетия и забытые на время направления опять становятся современными и модными. Основных модных течений в ювелирных украшениях в современном мире насчитывается три — это классический стиль, авангард и фольклорная тематика, которая связывает своё существование с геометрическими фигурами.

Многогранники достаточно актуальны в наше время. Они широко используются, в частности, для интерьера. В некоторых квартирах, стены выполнены в форме многогранника. Чтобы придать драгоценным камням красоту и игру цветов, их шлифуют, камню придают форму многогранника. Исходя из всех вышеперечисленных примеров, можно с уверенностью сказать, что многогранники есть вокруг нас!

Понятие многогранника: поверхность, составленная из многоугольников и ограничивающая некоторое геометрическое тело, называется многогранником.

Составные части многогранника:

1. Грани. Гранями называются многоугольники, из которых состоит многогранник.

2. Ребра. Стороны граней называются ребрами.

3. Вершины. Концы ребер – вершины многогранника.

Высшая категория кристаллов.

вольфрам

алмаз

германиум

золото.

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ АМУРСКОЙ ОБЛАСТИ УПРАВЛЕНИЕ ОБРАЗОВАНИЯ МУНИЦИПАЛИТЕТА ГОРОДА ТЫНДА МУНИЦИПАЛЬНОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ БЮДЖЕТНОЕ УЧРЕЖДЕНИЕ «СРЕДНЯЯ ОБЩЕОБРАЗОВАТЕЛЬНАЯ ШКОЛА № 7 ИМЕНИ ГЕРОЯ РОССИИ И.В.ТКАЧЕНКО»

ИССЛЕДОВАТЕЛЬСКАЯ РАБОТА

На тему:

« Многогранники в ювелирном деле»

По курсу:

Математика

Исполнитель: Миткеева Ирина ученица 9 « Г» класса.

Руководитель: Черныш Тамара Валентиновна .

Цель работы :

• Исследовать, как геометрические фигуры, в частности: многогранники, используются в ювелирном деле.

Задачи :

• Ознакомиться с многогранниками, их видами . Дать понятие правильных многогранников.

• Показать связь геометрии и драгоценных камней.

Гипотеза:

• Заключается в том, что наш мир не может существовать без многогранников, и их роль важна .

Актуальность темы:

• Современного человека вообще тяжело представить без драгоценностей. Сейчас достаточно мастерских по изготовлению и ремонту эксклюзивных изделий из драгметаллов, где каждый клиент сможет подобрать для себя необходимую услугу.
• Как во многих сферах человеческой деятельности, так и ювелирном искусстве существуют свои модные течение. Но все же проходят десятилетия и забытые на время направления опять становятся современными и модными. Основных модных течений в ювелирных украшениях в современном мире насчитывается три — это классический стиль, авангард и фольклорная тематика, которая связывает своё существование с геометрическими фигурами.

• Многогранники достаточно актуальны в наше время. Они широко используются, в частности, для интерьера. В некоторых квартирах, стены выполнены в форме многогранника. Чтобы придать драгоценным камням красоту и игру цветов, их шлифуют, камню придают форму многогранника. Исходя из всех вышеперечисленных примеров, можно с уверенностью сказать, что многогранники есть вокруг нас!

• Понятие многогранника: поверхность, составленная из многоугольников и ограничивающая некоторое геометрическое тело, называется многогранником.

• Составные части многогранника:
• 1. Грани . Гранями называются многоугольники, из которых состоит многогранник.
• 2. Ребра. Стороны граней называются ребрами.
• 3 . Вершины . Концы ребер – вершины многогранника.

Высшая категория кристаллов.

вольфрам

алмаз

германиум

золото

Средняя категория кристаллов.

цинк

графит

берилл

рубин

Низкая категория кристаллов.

слюда

медный купорос

гипс

рубин

александрит

топаз

СТАНОК ДЛЯ ОГРАНКИ КАМНЯ

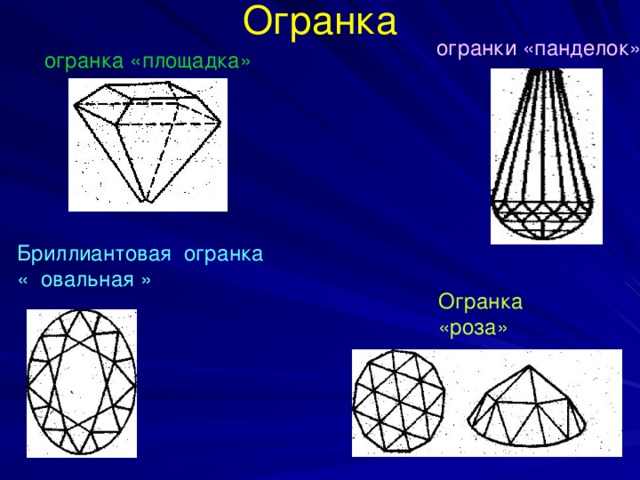
Огранка

огранки «панделок»

огранка «площадка»

Бриллиантовая огранка « овальная »

Огранка «роза»

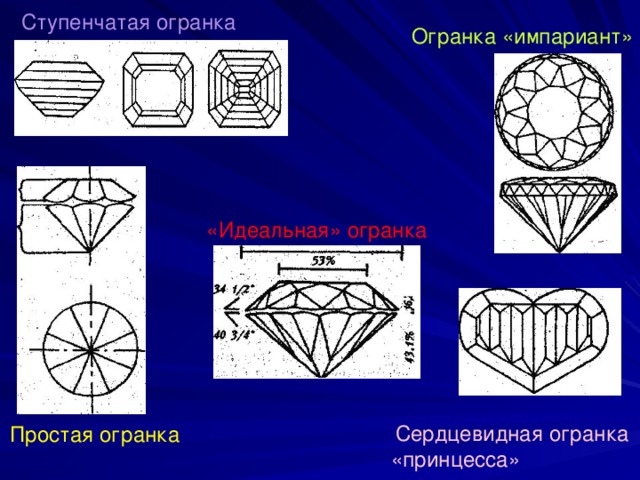
Ступенчатая огранка

Огранка «импариант»

«Идеальная» огранка

Сердцевидная огранка «принцесса»

Простая огранка

Выпуклые многогранники.

Многогранник называется выпуклым, если он весь расположен по одну сторону от плоскости каждой из его граней. Выпуклый многогранник называется правильным, если все его грани - одинаковые правильные многоугольники и все многогранные углы при вершинах равны. Существуют 5 видов правильных многогранников: тетраэдр, куб, октаэдр, додекаэдр, икосаэдр . (это доказал Евклид)

Тетраэдр - правильный четырехгранник . Он ограничен четырьмя равносторонними треугольниками (это - правильная треугольная пирамида).

Куб - Стороны граней именуются рёбрами куба. Всего их двенадцать, и каждое ребро принадлежит двум граням. Куб - хорошо знакомый нам многогранник, но не самый простой

Октаэдр - правильный восьмигранник .Он состоит из восьми равносторонних и равных между собой треугольников, соединенных по четыре у каждой вершины.

Додекаэдр - правильный двенадцатигранник, состоит из двенадцати правильных и равных пятиугольников, соединенных по три около каждой вершины .

Икосаэдр - имеет двадцать граней. Если каждую из них продолжить неограниченно, то тело будет окружено великим многообразием отсеков – частей пространства, ограниченных плоскостями граней. Все звездчатые формы икосаэдра можно получить добавлением к исходному телу таких отсеков.

Звездчатый октаэдр - восемь пересекающихся плоскостей граней .Это малые тетраэдры, основания которых совпадают с гранями октаэдра. Его можно рассматривать как соединение двух пересекающихся тетраэдров, центры которых совпадают с центром исходного октаэдра. Октаэдр имеет только одну звездчатую форму. Такой звездчатый многогранник в 1619 году описал Кеплер (1571-1630).

Многогранники вокруг нас

• Эти тела еще называют телами Платона.

Тетраэдр

Гексаэдр

Октаэдр

Додекаэдр

Икосаэдр

Ювелирная мастерская «ЗЛАТО»

Вывод:

• Моя гипотеза подтвердилась. По проведенной исследовательской работе можно сказать, что я, выполнив поставленные задачи и добившись цели, выяснила: что, действительно, многогранники играют не мало важную роль в окружающей среде и также важно их использование. Изучение многогранников занимает одну из важных тем и в геометрии. В этой работе я исследовала прекрасное с практикой, т.е. красоту ювелирного дела с математикой- геометрией.
• Думаю, я заинтересовала всех, и дала возможность открыть тайны огранки драгоценного камня у меня, надеюсь получилось.

Спасибо за внимание!

Список литературы.

• http://enc-dic.com/colier/Dragocenne-kamni-2796.html
• http://www.dragkamen.ru
• http://www.leto-doma.ru
• http://otebe.info/kamen.html
• а так же книги, учебники.