29.11.2024
- Элементы теории алгоритмов
Практические работы
1. Машина Тьюринга
Тренажёр «Машина Тьюринга» — это учебная модель универсального исполнителя (абстрактной вычислительной машины), предложенного в 1936 году А. Тьюрингом для уточнения понятия алгоритма. Согласно тезису Тьюринга, любой алгоритм может быть записан в виде программы для машины Тьюринга. Доказано, что машина Тьюринга по своим возможностям эквивалентна машине Поста и нормальным алгорифмам Маркова.
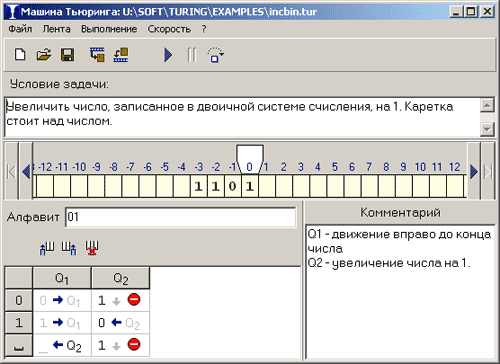
Машина Тьюринга состоит из каретки (считывающей и записывающей головки) и бесконечной ленты, разбитой на ячейки. Каждая ячейка ленты может содержать символ из некоторого алфавита A={a0,a1,…,aN}. Любой алфавит содержит символ «пробел», который обозначается как a0 или Λ. При вводе команд пробел заменяется знаком подчеркивания «_».
Машина Тьюринга — это автомат, который управляется таблицей. Строки в таблице соответствуют символам выбранного алфавита A, а столбцы — состояниям автомата Q={q0,q1,…,qM}. В начале работы машина Тьюринга находится в состоянии q1. Состояние q0 — это конечное состояние: попав в него, автомат заканчивает работу.
В каждой клетке таблицы, соответствующей некоторому символу ai и некоторому состоянию qj, находится команда, состоящая из трех частей:
символ из алфавита A;
направление перемещения: (вправо), (влево) или . (на месте);
новое состояние автомата
Наберите программу из учебника, которая увеличивает двоичное число на 1 и проверьте её работу.
Будет ли правильно работать эта программа, если вначале каретка расположена справа от числа? Почему?
Ответ:
Измените программу для увеличения двоичного числа на 1 так, чтобы она работала правильно, если вначале каретка расположена справа от числа.
|
| q1 | q2 |
| 0 | | 1 . q0 |
| 1 | | 0 |
| | q2 | 1 . q0 |
Опишите алгоритм работы программы для машины Тьюринга:
|
| q1 | q2 |
| а | q2 | |
| б | q2 | |
| | | q0 |
Ответ:
q1 –
q2 –
При каком начальном состоянии ленты и положении каретки эта программа зацикливается?
Ответ:
Лента:
Каретка:
Составьте программу для машины Тьюринга, которая заменяет в двоичном числе все 0 на 1 и все 1 на 0 (из числа 10101100 получается 01010011). Каретка находится слева от числа.
|
| q1 | q2 |
| 0 |
|
|
| 1 |
|
|
| |
|
|
Описание состояний:
q1 –
q2 –
Составьте программу для машины Тьюринга, которая умножает двоичное число на 2. Каретка находится над числом.
|
| q1 |
| 0 |
|
| 1 |
|
| |
|
Описание состояний:
q1 –
Составьте программу для машины Тьюринга, которая увеличивает троичное число на 1. Каретка находится справа от числа.
|
| q1 | q2 |
| 0 |
|
|
| 1 |
|
|
| 2 |
|
|
| |
|
|
Описание состояний:
q1 –
q2 –
При каком начальном положении каретки эта программа зацикливается?
Ответ:
Составьте программу для машины Тьюринга, которая уменьшает двоичное число на 1. Каретка находится над числом.
|
| q1 | q2 | q3 | q4 |
| 0 |
|
|
|
|
| 1 |
|
|
|
|
| |
|
|
|
|
Описание состояний:
q1 –
q2 –
q3 –
q4 –
При каком начальном положении каретки эта программа зацикливается?
Ответ:
2. Машина Поста
Тренажёр «Машина Поста» — это учебная модель универсального исполнителя (абстрактной вычислительной машины), основанного на работах Э.Л. Поста по уточнению понятия алгоритма. Согласно тезису Поста, любой алгоритм может быть записан в виде программы для машины Поста. Доказано, что машина Поста по своим возможностям эквивалентна машине Тьюринга и нормальным алгорифмам Маркова.
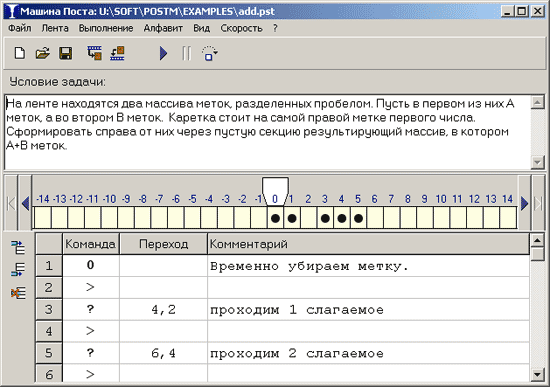
Машина Поста состоит из каретки (считывающей и записывающей головки) и бесконечной ленты, разбитой на ячейки. Каждая ячейка ленты может быть либо пустой («0»), или содержать метку («1»).
Программа состоит из пронумерованных строк. В каждой строке записывается одна из следующих команд:
N переместить каретку вправо на 1 ячейку и перейти к строке с номером N;
переместить каретку влево на 1 ячейку и перейти к строке с номером N
0 N записать в текущую ячейку «0» (стереть метку) и перейти к строке с номером N
1 N записать в текущую ячейку «1» (поставить метку) и перейти к строке с номером N
? N, M если текущая ячейка содержит «0» (не отмечена), то перейти к строке с номером N, иначе перейти к строке M
. остановить программу
Номер строки перехода в командах , , 0 и 1 можно не указывать, при этом происходит переход к следующей строке.
Для завершения работы программы достаточно сделать переход на строку 0, например, так:
? 25, 0 остановить программу, если текущая ячейка содержит «1», иначе перейти к строке 25.
Что делает следующая программа для машины Поста?
| 1 | |
| 2 | ? 3,4 |
| 3 | 1 1 |
| 4 | стоп |
Ответ:
Как она будет работать при различных начальных состояниях ленты?
Ответ:
Напишите программу для машины Поста, которая неприменима (то есть зацикливается) при любом начальном состоянии ленты.
| 1 |
|
| 2 |
|
| 3 |
|
Напишите программу для машины Поста, которая увеличивает на 1 число, записанной в унарной системе счисления. Каретка стоит над первой (самой левой) отметкой.
| 1 |
|
| 2 |
|
| 3 |
|
| 4 |
|
Решите задачу 2 при условии, что в начале работы каретка расположена где-то справа от записи числа.
| 1 |
|
| 2 |
|
| 3 |
|
| 4 |
|
| 5 |
|
Напишите программу для машины Поста, которая уменьшает на 1 число, записанной в унарной системе счисления. Каретка стоит над первой (самой левой) отметкой.
| 1 |
|
| 2 |
|
| 3 |
|
| 4 |
|
| 5 |
|
На ленте расставлены метки, между которыми могут быть пропуски длиной в одну ячейку. Заполнить все пропуски метками. Каретка стоит над самой левой меткой.
3.Нормальные алгорифмы Маркова (НАМ)
Тренажёр «Нормальные алгорифмы Маркова» — это учебная модель универсального исполнителя, предложенного в 1940-х годах А.А. Марковым для уточнения понятия алгоритма. Марков предположил, что любой алгоритм может быть записан в виде нормального «алгорифма» (учёный считал, что правильно произносить это иностранное слово именно так). Позднее было доказано, что нормальные алгорифмы Маркова эквивалентны по своим возможностям другим универсальным исполнителям: машине Тьюринга и машине Поста.
Нормальный алгорифм задает метод преобразования строк с помощью системы подстановок. Каждая подстановка состоит из слова-образца и слова-замены, разделенных цепочкой символов «-». На каждом шаге замены подстановки просматриваются по порядку сверху вниз, и выполняется первая из них, которая подошла: первое найденное слово-образец рабочей строки заменяется на слово-замену.
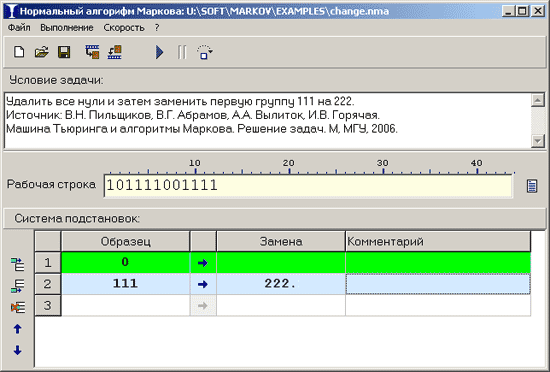
Слова слева и справа от знака «-» могут быть (а могут и не быть) заключены в апострофы или двойные кавычки. Следующие подстановки равносильны и определяют замену буквы «а» на сочетание «бв»:
а - бв
'а' - 'бв'
"а" - "бв"
'а' - "бв"
Левая часть (слово-образец) может отсутствовать, в этом случае слово-замена ставится в самое начало рабочего слова. Обычно такая замена должна стоять последней в списке подстановок (иначе происходит зацикливание).
Правая часть подстановки тоже может отсутствовать (при стирании образца).
Символ «.» после слова-замены обозначает терминальную подстановку, после которой выполнение алгоритма заканчивается. Например:
'а' - 'б'. заменить «а» на «б» и остановить программу
* - . стереть знак «*» и остановить программу
Что делает следующий НАМ, если применить его к символьной цепочке, состоящей из нулей и единиц:
| *0 0* *1 1* * =. * |
Ответ:
Как будет работать этот алгоритм при различных начальных состояниях ленты?
Ответ:
Напишите НАМ, который «сортирует» цифры двоичного числа так, чтобы сначала стояли все нули, а потом – все единицы.
Ответ:
Напишите НАМ, который удаляет последний символ строки, состоящей из цифр 0 и 1. Какую операцию он выполняет, если рассматривать строку как двоичную запись числа?
Ответ:
Напишите НАМ, который умножает двоичное число на 2, добавляя 0 в конец записи числа.
Ответ:
Напишите НАМ, который переводит число из двоичной системы счисления в единичную (унарную).
Ответ:
Дано слово, состоящее из букв «а», «б» и пробелов. Постройте нормальный алгоритм Маркова, который символы «а» переносит влево, символы «б» – вправо, а пробелы оставляет посередине.
Ответ:

 Получите свидетельство
Получите свидетельство Вход
Вход












 Практическая работа по теме "Алгоритмические машины" (679.35 KB)
Практическая работа по теме "Алгоритмические машины" (679.35 KB)
 0
0 155
155 8
8 Нравится
0
Нравится
0


