Платоновы тела и применение в строительстве

Презентация к конкурсу «Рубежи науки»

Тема: Платоновы тела и применение в строительстве

Выполнил работу студент группы С13-20: Милидонов Илья Владимирович

Преподаватель: Лаврентьева Татьяна Николаевна

КОД СПЕЦИАЛЬНОСТИ: 08.02.01 Чебоксарский техникум строительства и ГОРОДСКОГО хозяйства

Цель проекта:

Рассказать о правильных многогранниках, о их происхождении, их нахождении в природе, архитектуре и живописи.

История правильных многогранников

Их изучали ученые, ювелиры, священники, архитекторы. Этим многогранникам даже приписывали магические свойства. Древнегреческий ученый и философ Платон (IV–V в до н. э.) считал, что эти тела олицетворяют сущность природы. В своем диалоге «Тимей» Платон говорит, что атом огня имеет вид тетраэдра, земли – гексаэдра (куба), воздуха – октаэдра, воды – икосаэдра. В этом соответствии не нашлось места только додекаэдру и Платон предположил существование еще одной, пятой сущности – эфира, атомы которого как раз и имеют форму додекаэдра. Ученики Платона продолжили его дело в изучении перечисленных тел. Поэтому эти многогранники называют платоновыми телами.

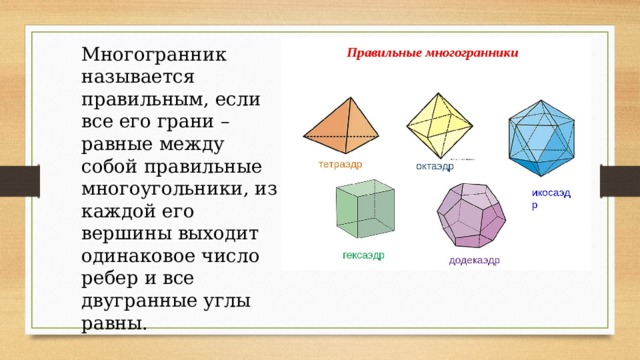
Многогранник называется правильным, если все его грани – равные между собой правильные многоугольники, из каждой его вершины выходит одинаковое число ребер и все двугранные углы равны.

Тетра́эдр — простейший многогранник, гранями которого являются четыре треугольника. Тетраэдр является треугольной пирамидой при принятии любой из граней за основание. У тетраэдра 4 грани, 4 вершины и 6 рёбер. Тетраэдр, у которого все грани — равносторонние треугольники, называется правильным. Сумма плоских углов при каждой вершине равна 180º

Правильный тетраэдр

Куб — правильный многогранник, каждая грань которого представляет собой квадрат. Составлен из 6 квадратов. Сумма плоских углов при каждой вершине равна 270º.

Правильный куб

(гексаэдр)

Окта́эдр — многогранник с восемью гранями. Пра́вильный окта́эдр является одним из пяти выпуклых правильных многогранников, так называемых платоновых тел; его грани — восемь равносторонних треугольников. Сумма плоских углов при каждой вершине 240º

Правильный октаэдр

Правильный икосаэдр:

Икосаэдр — это многогранник с 20 гранями. Существует бесконечно много непохожих икосаэдров, некоторые из которых имеют больше симметрий, другие меньше. Наиболее известен правильный икосаэдр — один из правильных многогранников, гранями которого являются 20 правильных треугольников. Сумма углов при каждой вершине равно 300º

Правильный додекаэдр

Пра́вильный додека́эдр — один из пяти возможных правильных многогранников. Додекаэдр составлен из двенадцати правильных пятиугольников, являющихся его гранями. Каждая вершина додекаэдра является вершиной трёх правильных пятиугольников. Таким образом, додекаэдр имеет 12 граней, 30 рёбер и 20 вершин. Сумма плоских углов при каждой вершине равна 324º

Применение в строительстве

Куб

Есть очень много зданий, которые используют куб как основную форму. Одним из наиболее ярких примеров может служить жилой дом по улице Петрова в г. Чебоксары

Тетраэдр

В современной архитектуре встречаются шедевры на основе тетраэдра. Стеклянная пирамида Лувра во дворе Наполеона служит главным входом в Лувр и является одним из символов Парижа. Примечателен и Офис Словацкого радио в виде перевёрнутой пирамиды. Здание было построено в 1969-1984 годах, архитектором Ш. Дюрковичем,Б. Кислингом и Ш. Светко.

Стеклянная пирамида Лувра

Офис Словацкого радио

Икосаэдр

Первым геодезическим куполом на основе икосаэдра стал открытый 18 июля 1926 года в Йене планетарий имени Цейса, созданный немецким инженером Вальтером Бауэрсфельдом. Однако истинную революцию в инженерии произвёл Ричард Бакминстер Фуллер, спроектировав пространственную конструкцию «геодезического купола». Но самое известное использование икосаэдра, вероятно, Павильон США на Экспо-67, ныне музей «Биосфера».

Планетарий им. Цейса

«Геодезический купол»

Музей «Биосфера»

Многогранники в кристаллах:

Правильные многогранники – самые выгодные фигуры, поэтому они широко распространены в природе. Подтверждением служит форма некоторых кристаллов:

Кристалл поваренной соли в форме гексаэдра(куба)

Кристалл алюмо-калиевого кварца имеет форму октаэдра

Кристалл сернистого колчедана имеет форму додекаэдра

Кристалл сурьменистого сернокислого натрия имеет форму тетраэдра

Интересно!!!

Икосаэдр оказался в центре внимания биологов в их спорах относительно формы вирусов. Вирус не может быть совершенно круглым, как считалось ранее. Чтобы установить его форму, брали различные многогранники, направляли на них свет под теми же углами, что и поток атомов на вирус. Оказалось, что только один многогранник дает точно такую же тень - икосаэдр.

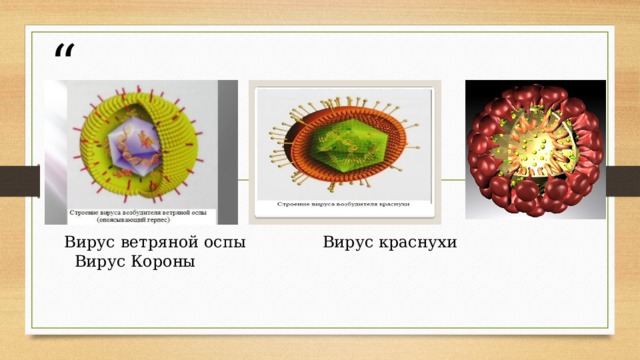
Вирус ветряной оспы Вирус краснухи Вирус Короны

За информацию огромное спасибо сайтам:

https://sites.google.com/site/stereometriaru/mnogogranniki/mnogogranniki-v-prirode

https://docplayer.ru/71184995-Aktualnost-platonovyh-tel-v-sovremennoy-arhitekture-i-stroitelstve-n-e-baumana.html

http://www.myshared.ru/slide/1082595/

https://mnogogranniki.ru/platonovy-tela.html