| Раздел долгосрочного планирования: 8.1А Многоугольники. Исследование четырехугольников. | Школа: КГУ «Чермошнянская средняя школа» Тайыншинский район СКО | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Дата : | ФИО учителя: Борович Ольга Вениаминовна | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| класс: 8 | Участвовали: | Не участвовали: | |||||||||||||||||||||||||||||||||||||||||||||||||||||
| Тема урока: | Признаки параллелограмма | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Цели обучения, достигаемые на этом уроке (Ссылка на учебный план) | 8.1.1.5 Выводить и применять признаки параллелограмма | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Цель урока | Все: формулируют признаки параллелограмма из свойств; определяют является ли четырехугольник параллелограммом на основе признаков; Большинство: применяют признаки параллелограмма при решении задач на доказательство; Некоторые: доказывают признаки параллелограмма; определяют необходимое и достаточное условие существование параллелограмма | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Уровни навыков мышления | Знание, понимание, применение | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Критерии оценивания | Выводят признаки параллелограмма; Различают три признака параллелограмма; находят в четырехугольнике равные отрезки, находят в четырехугольнике параллельные стороны, устанавливают причинно- следственные связи; применяют признаки параллелограмма при решении задач на доказательство; устанавливают необходимое условие существования параллелограмма; устанавливают достаточное условие существования параллелограмма | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Языковые задачи
| Языковая цель обучения: Учащиеся будут: -формулировать определение параллелограмма; -формулировать свойства параллелограмма; Формулировать теорему обратную свойству параллелограмма Комментировать ход решения задачи Предметная лексика и терминология: Свойство; признак; прямая и обратная теорема, доказательство признака; применение признака Серия полезных фраз для диалога/ письма Параллельные стороны, противолежащие стороны, противолежащие углы, равные стороны, равные углы, если____ то, свойство фигуры, признак фигуры, признак параллелограмма | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Воспитание ценностей
| Воспитание Национального единства, мира и согласия в нашем обществе через этот урок осуществляется путем формирования ценностей: равные права у всех при работе в группах; взаимоуважение и взаимовыручка при работе в парах и группах, воспитание лидерских качеств: через распределение ролей при работе в группах; через систему разноуровневых заданий | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Межпредметная связь | Внутрипредметная | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Предыдущие знания
| Определение параллелограмма, свойства параллелограмма. Условие и заключение теоремы. Прямая и обратная теорема. Справедливость обратной теоремы, доказательство теоремы Для вывода признака фигуры необходимо поменять местами условие и заключение в теореме, выражающей свойство фигуры; установить справедливость новой теоремы, доказать ее на основе имеющихся знаний | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Ход урока | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Запланированные этапы урока | Виды упражнений, запланированных на урок:
| Ресурсы | |||||||||||||||||||||||||||||||||||||||||||||||||||||
| Вызов.
Целеполагание
| Приветствие. Объединение в группы приемом «Песочница» Эффективность: Прием позволяет заранее распределить учащихся на группы примерно равных возможностей, но так чтобы в каждой группе оказался ученик с повышенной мотивацией и низкой мотивацией. Повторение правила работы в группе, распределение ролей в группе. При помощи «Магического стула» лидеры групп получают задания для работы в группе: Актуализация опорных знаний: I-группа Задание1 «Объясните смысл понятия-свойство фигуры. Перечислите свойства параллелограмма » II-группа Задание1 «Объясните смысл понятия-обратная теорема. Всегда ли верна обратная теорема? Приведите пример верной и неверной обратной теоремы» III-группа Задание1 «Объясните смысл понятия- признак. Перечислите признаки параллельных прямых » Взаимопроверку выполненного задания учащиеся выполняют приемом «Карусель», с последующей защитой постеров Цель: Повторение и систематизация материала необходимого для изучения нового материала Эффективность приема: - актуализация знаний; - повторение большого объема информации за малый промежуток времени - развитие коммуникативных навыков в процессе работы в группах - взаимоуважение и взаимовыручка при работе в группах, воспитание лидерских качеств. ФО прием «В чем разница?» Учитель: Определите разницу между понятиями «свойство фигуры» и «признак фигуры»; между понятиями «прямая теорема» и «обратная теорема» Предполагаемые ответы учащихся: -Свойства и признак взаимно- обратные теоремы На прошлом уроке вами были изучены свойства параллелограмма. Как вы считаете, какова цель урока? Предполагаемые ответы учащихся: Изучить признаки параллелограмма Учитель вместе с учащимися формулирует цель урока -Вывести признаки параллелограмма и научиться применять их при решении задач Учитель: У каждого предмета есть признаки, которые отличают его от других предметов. Важно помнить, что признаки предмета могут быть существенными и несущественными. Рассмотрим пример: В желтом четырехугольнике диагонали точкой пересечения делятся пополам. Можно ли утверждать что этот четырехугольник параллелограмм? Что в условии существенно? Что несущественно? |
| |||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Осмысление
Применение | Задание 2. Работы в группах: На основе свойств параллелограмма, выведите признаки параллелограмма. Заполните таблицу. Прием: «Конструктор события» Цель: Формирование умений сравнивать, устанавливать причинно-следственные связи.
Критерии: -Признаки существенные; -Формулировки четкие, не содержащие лишней информации Защита постеров, взаимооценивание прием «Две звезды, одно пожелание» Эффективность приема: -Внимательно слушают, что способствует лучшему запоминанию; - Оценивают на основе критериев; -Сопоставляют, сравнивают, анализируют, чтобы сформулировать пожелание. -устанавливают причинно-следственные связи Учитель обобщает, делает вывод Задачи, на готовых чертежах
|
Слайд презентации
Л.С.Атанасян Геометрия 7-9 Учебник для Общеобразовательных учреждений; 2002г
| |||||||||||||||||||||||||||||||||||||||||||||||||||||
| |
Задание Доказать:
ФО прием : «Внутренний и внешний круг» Вопросы: Ученик ученику; учитель ученику. Эффективность приема: взаимообучение и взаимоконтроль; вовлечение всех обучающихся в процесс обучения; коррекция знаний учащиеся двигаются, меняется вид деятельности, заменяет разминочные упражнения для поддержания здоровья обучающихся Задание 3 для работы в группах: Из вершин B и D параллелограмма ABCD, у которого AB и BC не равны и угол А острый, проведены перпендикуляры ВК и DM к прямой АС. Докажите, что четырехугольник BMDK – параллелограмм.
ФО прием «Светофор» Индивидуальная работа по карточкам: Карточка А Задание 1
Задание 2 В четырехугольнике MNPQ диагонали в точке пересечения делятся пополам. Доказать, что четырехугольнике MNPQ параллелограмм Обозначить точку пересечения диагоналей О 2.Рассмотреть треугольники, найти равные (указать в треугольниках равные элементы) 3. Определить признак параллельности прямых, вытекающий из равенства углов треугольника
Карточка В Задание 1. Дано: АВСD – четырехугольник, AD=BC,АЕ- биссектриса угла А,
Доказать: АВСD- параллелограмм
Задание 2 Докажи один из признаков параллелограмма
Карточка С Задание 1 На сторонах AB, BC, CD и DA четырехугольника ABCD отмечены соответственно точки M, N, P и Q так, что AM=CP, BN=DQ, BM=DP, NC=QA. Докажите, что ABCD и MNPQ — параллелограммы. Задание 2 Докажи один из признаков параллелограмма
ФО прием «Светофор» Домашнее задание: А) Выучить признаки параллелограмма; Задача: Точки К и М принадлежат диагонали BD параллелограмма ABCD, причем BK=MD. Определите, является ли четырехугольник AKCM параллелограммом?
В) Выучить признаки параллелограмма, Задача: Пусть Е- середина стороны ВС, а F-середина стороны AD параллелограмма ABCD. Докажите, что четырехугольник BEDF-параллелограмм.
С) Решите задачи с использованием признака (признаков) параллелограмма Задача 1. Через точку пересечения диагоналей параллелограмма проведена прямая. Докажите, что отрезок ее, заключенный между параллельными сторонами, делится в этой точке пополам. Задача 2. Найдите периметр параллелограмма, если биссектриса одного из его углов делит сторону параллелограмма на отрезки 7 см и 14 см. |
Л.С.Атанасян Геометрия 7-9 Учебник для Общеобразовательных учреждений; 2002г
https://www.kursoteka.ru/course/5313/lesson/19922/unit/50482
http://www.mathematics-repetition.com/tag/zadatchi-na-primenenie-priznakov-parallelogramma
Л.С.Атанасян Геометрия 7-9 Учебник для Общеобразовательных учреждений; 2002г
Л.С.Атанасян Геометрия 7-9 Учебник для Общеобразовательных учреждений; 2002г
Л.С.Атанасян Геометрия 7-9 Учебник для Общеобразовательных учреждений; 2002г
http://www.mathematics-repetition.com/tag/zadatchi-na-primenenie-priznakov-parallelogramma
Ж.Кайдасов и др.Геомет.Учебник для 8 кл, общеобразовательной школы Алматы:Мектеп2016г
Д.Юсупов, С.Заурбеков геометрия 8, Аматы: Мектеп 2012г
Д.Юсупов, С.Заурбеков геометрия 8, Аматы: Мектеп 2012г
| |||||||||||||||||||||||||||||||||||||||||||||||||||||
| Рефлексия
| Прием «Телеграмма». Учитель раздает учащимся бланки телеграммы Инструкция: -Напишите телеграмму своему другу или подруге, которых будем считать, что на уроке не было -Расскажите ему (ей), чему вы научились на уроке -Было ли интересно, и т. -Текст телеграммы начните со слов: Сегодня на уроке я узнал… |
| |||||||||||||||||||||||||||||||||||||||||||||||||||||
| Дифференциация – каким способом вы хотите больше оказывать поддержку? Какие задания вы даете ученикам более способным по сравнению с другими? | Оценивание – как Вы планируете проверять уровень усвоения материала учащимися? | Охрана здоровья и соблюдение техники безопасности | |||||||||||||||||||||||||||||||||||||||||||||||||||||
| Дифференциацию на уроке начинаю с постановки цели урока с учетом потребностей обучающихся (все; большинство; некоторые). Задания на урок подбираю с учетом ступенчатости: от простого к сложному, с учетом дифференциации- учетом потребностей. Так как в классе есть обучающиеся с высокой и низкой мотивацией, для их поддержки использую способы : распределение ролей при работе в группе; свободный выбор обучающимися уровня сложности задания(А; В;С); Домашнее задание составляю с учетом дифференциации: трех уровней сложности, что позволит обучающемуся самому определить уровень сложности и определить самому свою зону ближайшего развития. | С целью оценивание для обучения применяю различные техники формативного ценивания: Прием «Внешний и внутренний круг»- взаимооценка усвоения теоретического материала по вопросам; Прием «Светофор» сигнальные карточки об уровне усвоенных знаний; Прием «Телеграмма»-самооценка учащимся результатов своей деятельности на уроке
Оценивание на основе критериев: Прием «Две звезды, одно пожелание» К каждой задаче на применение признаков параллелограмма, на доказательство разрабатываю критерии оценивания и дескрипторы к ним
| Активные методы обучения планируемые на урок позволят менять деятельность учащихся, что способствует снижению утомляемости, лучшему усвоению материала Пункты Правил техники безопасности Правила работы в группе; При применении методов связанных с перемещениями по классу напоминаю правила поведения в школе; | |||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| Используйте данный раздел урока для рефлексии. Ответьте на вопросы, которые имеют важное значение в этом столбце. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Итоговая оценка
Какие две вещи прошли действительно хорошо (принимайте в расчет, как преподавание, так и учение)? 1: 2: Какие две вещи могли бы улучшить Ваш урок (принимайте в расчет, как преподавание, так и учение)? 1: 2: Что нового я узнал из этого урока о своем классе или об отдельных учениках, что я мог бы использовать при планировании следующего урока? | |||||||||||||||||||||||||||||||||||||||||||||||||||||||

 Получите свидетельство
Получите свидетельство Вход
Вход






 B C
B C
 F
F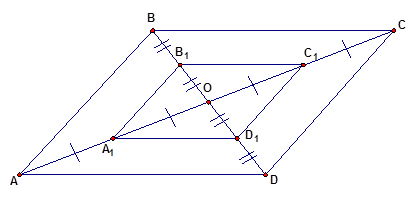










 План урока по геомерии в 8 классе "Признаки параллелограмма" (119.79 KB)
План урока по геомерии в 8 классе "Признаки параллелограмма" (119.79 KB)
 0
0 260
260 31
31 Нравится
0
Нравится
0


