План урока информатики и презентация на тему Метод Крамера

И в шутку, и в серьёз…

•   За сколькими зайцами нельзя угнаться? 

(За двумя.)

• - Какая нога собаке ни к чему?

(Пятая.)

• - Золотое колесо в синем небе?

(Солнце.)

• - Сколько цифр в двоичной системе счисления? 

(2)

• - Назовите три последние буквы алфавита. 

(э, ю, я.)

• - Какой сегодня день?

  (Пятница, 16 ноября.)

16.11.2018

Решение системы линейных уравнений методом Крамера

Урок информатики в 12-А классе

Учитель II дид. категории

Гоя М.А.

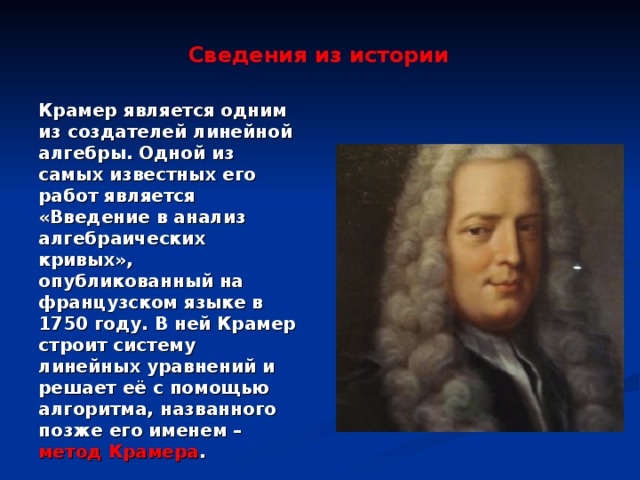
Сведения из истории

Крамер является одним из создателей линейной алгебры. Одной из самых известных его работ является «Введение в анализ алгебраических кривых», опубликованный на французском языке в 1750 году. В ней Крамер строит систему линейных уравнений и решает её с помощью алгоритма, названного позже его именем – метод Крамера .

Дана система

Составляем и вычисляем:

Если Δ≠ 0, тогда система имеет

одно единственное решение.

Формулы Крамера

………… .

Заменяя столбец с коэффициентами соответствующей переменной свободными членами:

Решение системы методом Крамера

Решение. Находим определители системы:

Ответ: (1; 0; -1) .

Программирование на языке Паскаль

метода Крамера:

1)Для матрицы, составленной из коэффициентов при неизвестных , нам нужен двумерный массив А( n*n) с элементами реального или целого типа;

( array[1..n,1..n] )

2) Одномерный массив b с элементами реального или целого типа для свободных членов системы; ( array[1..n] );

3) Одномерный массив x с элементами реального типа – решения системы.

( x 1 , x 2 , … , x n )

Учесть условия:

• Определитель системы не равен 0.
• Δ 1 , Δ 2 , …, Δ n получаются заменяя элементы первого, второго, и т.д. n - го столбца элементами столбца свободных членов.
• Решения получаем по формулам:

………… .

Практическая часть

Решите системы:

Для чётных ПК

Для нечётных ПК

Рефлексия

• Подумайте, что мог бы сказать Крамер, присутствуя на нашем уроке сегодня?
• Что было самым интересным на уроке?
• Что было самым трудным?
• Что вы расскажете, если вас спросят, что вы проходили сегодня на уроке информатике?
• С какой мыслью уходите сегодня с урока?

Домашнее задание:

• П. 4.2. стр.42-44
• Вспомнить метод Гаусса
• *упр.3 стр.45