Цели в блоках достижений:
Личностных результатов:
1. самопознание;
2. формирование целостного мировоззрения;
3. креативность мышления, инициатива, находчивость, активность при решении математических задач.
Метапредметных результатов:
1. представление о том, где используется перпендикулярность в реальной жизни.
2. умение самостоятельно ставить цели, выбирать и создавать алгоритмы для решения учебных математических задач по данной теме;
3. умение видеть математическую задачу в контексте проблемной ситуации в других дисциплинах, в окружающей жизни;
Этапы урока (распределение времени).
1. Организационный момент (1-2 минуты).
2. Актуализация знаний (4-5 минут)
3. Формулировка темы урока (6-7 минут)
4. Объяснение нового материала. (8-10 минут)
5. Решение задачи на распознавание. (9-10 минут)
6. Закрепление изученного материала. (7-8 минут)
7. Подведение итогов. Домашнее задание. (2-4 минут)
Ход урока.
1. Приветствие учеников:
Здравствуйте, ребята. А теперь посмотрите на своего соседа за партой, улыбнитесь ему и еще раз поздоровайтесь с ним.
2. Название нашего урока «Принцип архитектуры планеты Земля».
Посмотрите на картины, (на экране появляются исторические достопримечательности г. Симферополь, приложение 1) на них изображен исторический и современный Симферополь

Кинотеатр «Симферополь», улица Пушкина, здание цирка, железнодорожный вокзал, на второй картине, точнее на фото изображен уже современный Симферополь.
Задает вопрос:
Несмотря на историческое различие в облике Симферополя
- есть общий принцип построения любого здания на планете Земля. Что это за принцип?
Записывает на доске некоторые гипотезы, имеющие отношение к геометрии.
Какая из гипотез была близка к моей версии выясним позднее. Более того, Вы сами определите ее после того как, мы вспомним некоторые стереометрические понятия.
Проведем небольшой устный опрос:
1. Что называется углом между прямыми?
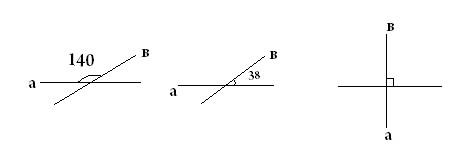
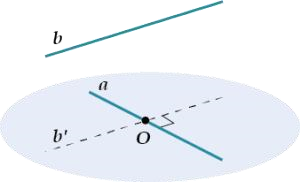
2. Чему равны углы между прямымиа и b:
3. Что называется углом между скрещивающимися прямыми?
4. Как найти угол между скрещивающимися прямыми?
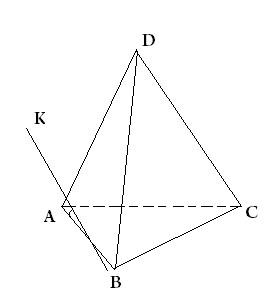
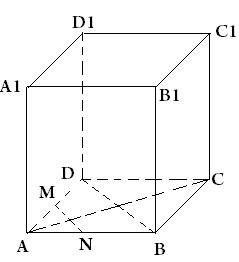
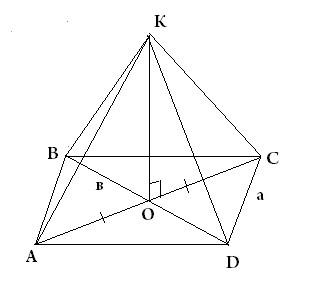
5. Дан тетраэдр DABC. Чему равен угол между DC и AB, если КМ || DC, М принадлежит АВ, КМА = 96?
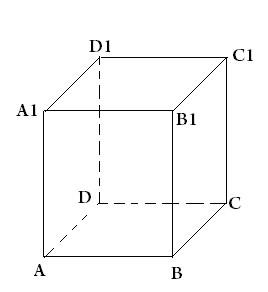
6. Что называется кубом? Перечислите его свойства.
Возвратимся к картинам, посмотрите на 1-ой появились прямые, скажите в каком соотношении находятся данные прямые? (учащиеся выдвигают гипотезы) Правильно, Розовая и синяя, красная и зеленая, голубая и фиолетовые линии перпендикулярны, потому что угол между ними равен 90 градусам.
Давайте далее посмотрим на других картинах, где перпендикулярные прямые?
Так почему перпендикулярность основной принцип архитектуры Земли? ( Геометрия в архитектуре является очень важной наукой.
В построении таких высоких здании как например Эйфелева башня (башня.jpg)
Весь материал - в документе.

 Получите свидетельство
Получите свидетельство Вход
Вход



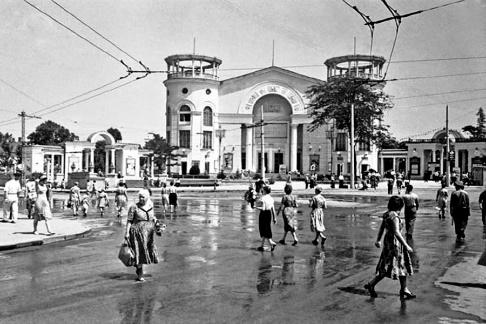












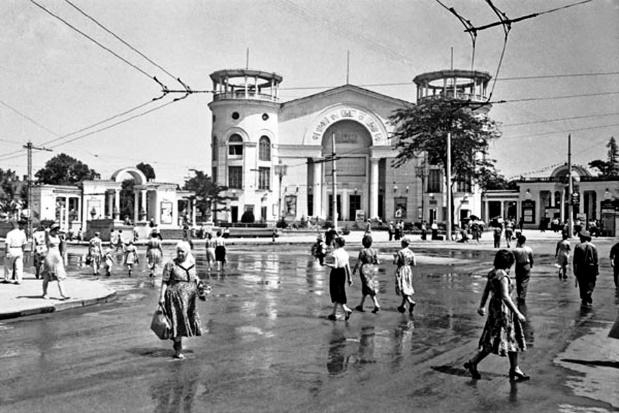









 План-конспект урока по геометрии "Перпендикулярные прямые в пространстве. Параллельные прямые, перпендикулярные к плоскости" (1.3 MB)
План-конспект урока по геометрии "Перпендикулярные прямые в пространстве. Параллельные прямые, перпендикулярные к плоскости" (1.3 MB)
 0
0 2177
2177 447
447 Нравится
0
Нравится
0




