Педагогическая разработка по теме: "Применение различных способов разложения многочленов на множители"

Открытый урок алгебры

в 7Г классе учитель математики

Ерёменко Н.А.,

МАОУ «СОШ №40 с уиоп»

г. Набережные Челны, 07.02.2018г.

Среди наук из всех главнейших,

Важнейшая всего одна.

Учите алгебру, она глава наукам,

Для жизни очень всем нужна.

Когда достигнешь ты наук

высоты,

Познаешь цену знаниям своим,

Поймешь, что алгебры красоты,

Для жизни будут кладом не плохим .

Представление многочлена в виде суммы двух или нескольких многочленов .

Разложение многочлена на множители –это…

Представление многочлена в виде произведения двух или нескольких одночленов .

Представление многочлена в виде произведения двух или нескольких многочленов.

ФОРМУЛЫ СОКРАЩЕННОГО УМНОЖЕНИЯ

квадрат суммы

квадрат разности

разность квадратов

сумма кубов

разность кубов

куб суммы

куб разности

• квадрат суммы квадрат разности разность квадратов сумма кубов разность кубов куб суммы куб разности

( a + b ) ² = a ² + 2 ab + b ²

( a – b ) ² = a ² – 2 ab + b ²

a ² – b ²= ( a – b ) ( a + b )

a³ + b³ = ( a + b )( a² – ab + b² )

a³ – b³ = ( a – b )( a ² + ab + b²

( a + b ) ³ = a³ + 3a² b + 3ab² + b³

( a – b ) ³ = a ³ – 3a² b + 3ab² – b³

№

ФОРМУЛА

1

(x+3)²

2

x²-16

№

3

(2x-3)(2x+3)

1

ОТВЕТ

4

4x²-9

2

БУКВА

81-18x+x²

5

(4x-5y)²

3

О

6

16x²-40xy+25y²

7

25x²-49y²

4

(x-4)(x+4)

А

9y²+36yx+36x²

5

И

(3y+6x)²

6

x²+6x+9

Т

Д

7

(9-x)²

Ф

(5x-7y)(5x+7y)

Н

Диофант

ИСТОРИЧЕСКАЯ СПРАВКА

Очень давно, в Древней Греции жили и

работали замечательные ученые-

математики, которые всю жизнь

отдали служению науке. В то время

все алгебраические утверждения

выражали в геометрической форме. Вместо сложения чисел говорили о сложении отрезков, а произведение двух чисел сравнивали с площадью, и трех чисел - с объемом и т.д.

ФСУ записывали не с помощью букв, а словами и доказывали геометрически.

Первым ученым, который отказался от геометрических способов выражения и перешел к алгебраическим был древнегреческий ученый-математик, живший в 3 веке до н.э. Диофант Александрийский. Появились формулы, которые стали называться ФСУ.

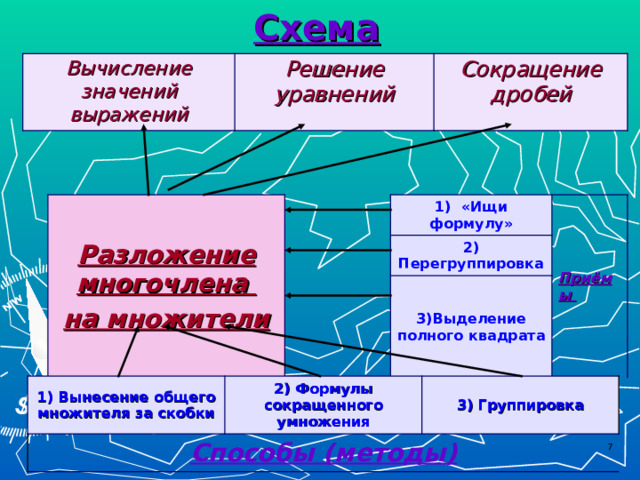
Схема

Вычисление значений выражений

Решение уравнений

Сокращение дробей

Разложение многочлена

на множители

1) «Ищи формулу»

2) Перегруппировка

Приёмы

3)Выделение полного квадрата

1) Вынесение общего множителя за скобки

Способы ( методы )

2) Формулы сокращенного умножения

3) Группировка

Тема « Применение различных способов разложения многочленов на множители».

ПРОВЕРКА ОТВЕТОВ

ПРОВЕРКА ОТВЕТОВ

ПРОВЕРКА ОТВЕТОВ

ПРОВЕРКА ОТВЕТОВ

ПРОВЕРКА ОТВЕТОВ

ПОРЯДОК ПРИМЕНЕНИЯ РАЗЛИЧНЫХ МЕТОДОВ ПРИ РАЗЛОЖЕНИИ МНОГОЧЛЕНА НА МНОЖИТЕЛИ

• Вынести общий множитель за скобку (если он есть).
• Попробовать разложить многочлен на множители по формулам сокращённого умножения.
• «Увидеть» и попробовать выделить полный квадрат.
• Попытаться применить способ группировки (если предыдущие способы не привели к цели).

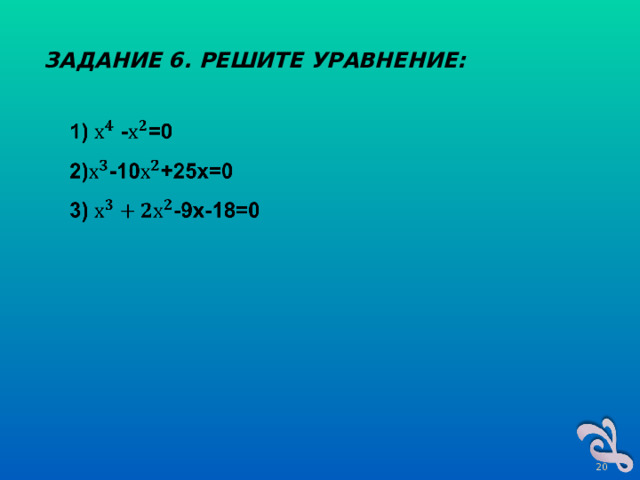
ЗАДАНИЕ 6. РЕШИТЕ УРАВНЕНИЕ:

ЗАДАНИЕ 6. РЕШЕНИЕ:

ЗАДАНИЕ 6. РЕШИТЕ УРАВНЕНИЕ:

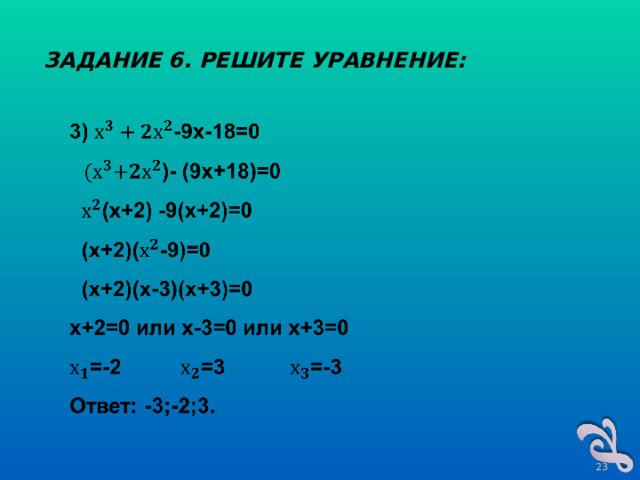
ЗАДАНИЕ 6. РЕШИТЕ УРАВНЕНИЕ:

Гора успеха

Мне урок очень понравился

Урок понравился ,но некоторые задания не понял(а)

Урок оставляю с прекрасным настроением

Узнал(а) много интересного на уроке

Доволен (довольна) своей оценкой

ДОМАШНЕЕ ЗАДАНИЕ

• П.19 ИЗУЧИТЬ, ВЫПОЛНИТЬ №708,710,712,714

В добрый час! Успехов вам! Успех-это 99% потения и 1% везения!!!