Памятка "Работа над задачами на движение"

Памятка «Учимся решать задач на движение»

В задачах на движение  рассматриваются три взаимосвязанные величины:

S - расстояние (пройденный путь),

t - время движения и

V - скорость – расстояние, пройденное за единицу времени.

Расстояние – это произведение скорости на время движения

S = V ● t

Скорость  - это частное от деления расстояния на время движения

V = S : t

Время – это частное от деления расстояния на скорость движения

t = S : V

Задачи на встречное движение

Скорость сближения – это сумма скоростей, движущихся навстречу друг другу тел. V сближ. = 1V + 2V

 Пример 1. Два велосипедиста одновременно выехали навстречу друг другу из двух посёлков и встретились через 3 часа. Первый велосипедист ехал со скоростью 12 км/ч, а второй – 14 км/ч. На каком расстоянии находятся посёлки?

Схема к задаче:

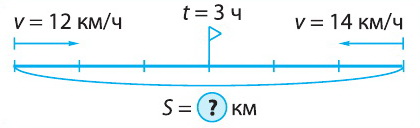
Решение:

S = V ● t

V сближ. = 1V + 2V

1 способ:

1) 12 • 3 = 36 (км) – проехал первый велосипедист до встречи

2) 14 • 3 = 42 (км) – проехал второй велосипедист до встречи

3) 36 + 42 = 78 (км)

2 способ:

1) 12 + 14 = 26 (км/ч) – скорость сближения

2) 26 • 3 = 78 (км)

Ответ: расстояние между посёлками 78 км.

 Пример 2. Из двух городов навстречу друг другу выехали две машины. Скорость первой – 80 км/ч, скорость второй – 60 км/ч. Через, сколько часов машины встретятся, если расстояние между городами 280 км?

Схема к задаче:

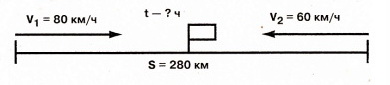
Решение:

V сближ. = 1V + 2V

t = S : V

1) 80 + 60 = 140 (км/ч) – скорость сближения

2) 280 : 140 = 2 (ч)

Ответ: машины встретятся через  2 часа.

 Пример 3. Из двух городов, расстояние между которыми 340 км, выехали одновременно навстречу друг другу две машины. Скорость первой – 80 км/ч. С какой скоростью ехала вторая машина, если встретились они через 2 часа?

Схема к задаче:

Решение:

V = S : t

2V = V сближ. - 1V

1) 340 : 2 = 170 (км/ч) – скорость сближения

2) 170 – 80 = 90 (км/ч)

Ответ: 90 км/ч. скорость второй машины

Задачи на движение в противоположных направлениях

Скорость удаления – это расстояние, которое проходят тела за 1 ч при движении в противоположных направлениях. 

V удал. = 1V + 2V

 Пример 1. Два лыжника одновременно вышли из пункта А в противоположных направлениях. Первый лыжник шёл со скоростью 12 км/ч, а второй – 14 км/ч. На каком расстоянии друг от друга они будут через 3 ч?

Схема к задаче:

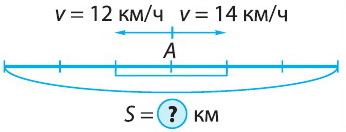
 Решение:

S = V ● t

1 способ

1)12 • 3 = 36 (км) – расстояние, которое прошёл первый лыжник за 3 ч

2)14 • 3 = 42 (км) – расстояние, которое прошёл второй лыжник за 3 ч

3)36 + 42 = 78 (км) 

2 способ

V удал. = 1V + 2V

S = V ● t

1)12 + 14 = 26 (км/ч) – скорость удаления

2)26 • 3 = 78 (км)

Ответ: через 3 ч они будут друг от друга на расстоянии 78 км.

 Пример 2. Из города в противоположных направлениях выехали две машины. Скорость первой – 80 км/ч, скорость второй – 60 км/ч. Через сколько часов расстояние между машинами будет 280 км?

Схема к задаче:

Решение:

V удал. = 1V + 2V

t = S : V

1) 80 + 60 = 140 (км/ч) – скорость удаления

2) 280 : 140 = 2 (ч)

Ответ: через 2 часа расстояние между машинами будет 280 км

Пример 3. Из города одновременно в противоположных направлениях выехали две машины. Скорость первой – 80 км/ч. С какой скоростью ехала вторая машина, если через 2 часа расстояние между ними было 340 км?

Схема к задаче:

Решение:

V = S : t

2V = V удал. - 1V

1) 340 : 2 = 170 (км/ч) – скорость удаления машин

2) 170 – 80 = 90 (км/ч)

Ответ: скорость второй машины 90 км/ч.