Открытый урок
Тема урока: «Системы линейных уравнений с двумя переменными.
Способ сложения».
Алгебра 7 класс
(учебник Ю.Н. Макарычев,Н.Г. Миндюк и др.)
Магамедова И.С.
Тема урока: «Системы линейных уравнений с двумя переменными. Способ сложения».
Цели урока:
Образовательные:
повторить понятие системы линейных уравнений с двумя переменными, ее решения, графический способ и способ подстановки;
выработать начальные навыки решения системы линейных уравнений способом сложения;
Развивающие:
развитие математической речи учащихся;
умения анализировать, сравнивать, сопоставлять;
развитие внимания, наблюдательности, памяти;
развитие познавательного интереса учащихся через введение исторического материала;
Воспитательные:
формирование таких качеств личности, как организованность, ответственность, аккуратность;
выработать умение анализировать проделанную работу и адекватно её оценивать.
Тип урока: комбинированный.
Ход урока.
Организационный момент.
Приобретать знания - храбрость,
Приумножать их - мудрость,
А умело применять - великое искусство!
Устная работа.
Вычислите: 42, (-6а)2, (-1)4, (-1)7.
Упростите: 5в+2в, -9а+9а, 3х-8х, 6у+у.
Выполните действия: (а+в)2=…
(х-у)2=…
(m+n)(m-n)=…
Согласны ли вы с решением следующего уравнения
3х - 5 = 7х - 3,
3х- 7х = -3- 5,
-4х = -8,
х =2. Ответ: х =2. ?
Проверка домашней работы.
№1070(а)
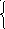
2х+у=12,
7х-2у=31;
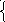
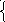
1)2х+у=12, 2)7х-2у=31, 3) х=5, х=5,
у=12-2х; 7х-2(12-2х)=31, у=12-2×5, у=2.
7х-24+4х=31,
7х+4х=31+24,
11х=55,
х=5;
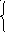
 Проверка: 2×5+2=12, 12=12, верное
Проверка: 2×5+2=12, 12=12, верное
7×5-2×2=31; 31=31, верное. Ответ:(5;2)
Что называется решением системы уравнений с двумя переменными?
Что значит решить систему уравнений?

2)Практическая работа (на масштабно-координатной бумаге).
Решить графически системы уравнений:
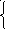 1) у +2х =1, 2) 2у + 4х = 6, 3) у - 3х = 5,
1) у +2х =1, 2) 2у + 4х = 6, 3) у - 3х = 5,
у – х = 3; у +2х = 3; у = 3х - 2.
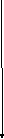
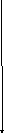
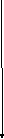 у у у
у у у



х х х
Выводы. Сколько решений может иметь система двух линейных уравнений с двумя переменными?

Актуализация опорных знаний.
Интеллектуальная разминка. Алгебраический софизм.
Алгебраические софизмы – намеренно скрытые ошибки в уравнениях и числовых выражениях.
Залог успеха - огромное внимание!
Я сейчас докажу, что
Два неодинаковых натуральных числа равны между собой!
Решим систему двух уравнений:
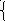 х + 2у = 6,
х + 2у = 6,
у = 4 - х/2
Сделаем это подстановкой у из 2го уравнения в 1, получаем
х+8-х=6, откуда 8=6.
Где же ошибка???
Второе уравнение можно записать как х+2у=8, так что исходная система запишется в виде:
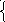 х+2у=6,
х+2у=6,
х+2у=8
В этой системе уравнений коэффициенты при переменных одинаковы, а правые части не равны между собой, из этого следует, что система несовместна, т.е. не имеет ни одного решения. Графически это означает, что прямые
у=3-х/2 и у=4-х/2 параллельны и не совпадают.
Перед тем, как решать систему линейных уравнений, полезно проанализировать, имеет ли система единственное решение, бесконечно много решений или не имеет решений вообще.
Задание.
Установите соответствие между прямыми (графиками линейных функций) и формулами, которыми заданы линейные функции.
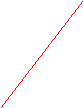
 у у = kх + m
у у = kх + m
 b d
b d



 a 1) y=2x+3;
a 1) y=2x+3;
2) y=3x-2;
0 х 3) у=-4х+5;
4) у=-2х-4.
с
Цифровой диктант.
Для рассмотрения предлагается 5 утверждений. Одни из них несут правильную информацию, другие – неточную или неверную. Если вы согласны, ставьте напротив утверждения цифру 1, если нет – 0. Результаты ответов составят пятизначное число, которое надо записать.
Пара значений переменных (х; у) является решением системы уравнений с двумя переменными, если она обращает каждое уравнение системы в верное равенство.
7а3в5х3. Коэффициент одночлена равен 7.
3х + у = 1,
-2х + 5у = 5; (0; 1) – решение системы уравнений
4) 6у + 4у = 10у.
3 •
1 точка пересечения прямых имеет координаты (3;1)
Ответ: 10110
Самостоятельная работа под копирку (с последующей самопроверкой)
В1 В2
Выразите в уравнениях: а) x через y,
б) у через х
х + у = 12; 1) х + у = 9;
х - 7у = 14. 2) у – 8х = -16.
Проверка:
В1 1) а) х = 12 - у, В2 1) а) х = 9 – у,
б) у = 12 – х; б) у = 9 – х;
2) а) х = 14+ 7у, 2) а) х = 2 + 1/8у,
б) у = -2 + 1/7х. б) у = -16+ 8х.
5) Физкультминутка.
1. Зарядка для глаз.
а) б)
в)
2. Игра «Великаны и карлики».
Если согласны с утверждением, то встаем и два раза хлопаем, если нет, то сидя мотаем головой (упражнение для мышц шеи)
4
6
Решая систему уравнений графически, я делаю вывод, что она имеет два решения х=6 и у=4.
-5х2у34=-20х2у3.
Уравнение 8ху + 5у = -1 не является линейным уравнением с двумя переменными.
Изображен график функции у = -2х-5.
9в – в = 8в.
Совершенствование знаний и умений.
№1083а) 5. Изложение нового
Способ подстановки. материала.Способ сложения.
х-6у=17, х - 6у =17, х=5
5х+6у=13; 5х+6у=13, 5-6у=17,
1)х=17+6у; 2)5(17+6у)+6у=13, 3) у =-2, 6х=30, -6у=17-5,
85+30у+6у=13, х=17+6*(-2) х=5; -6у=12
36у=-72, у=-2, х=5, у=2.
у=-2; х=5. У=2.
Ответ: (5;2) Ответ: (5;2)
№1083 в)
3х+2у=5,|*(-1) -3х-2у=-5, х=-5, х=-5,
-5х+2у=45; -5х+2у=45 3*(-5)+2у=5, у=10.
-8х=40, -15+2у=5,
х=-5; 2у=5+15,
2у=20,
у=10, Ответ: (-5;10)
№1084 а).
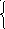 40х+3у=10, 1
40х+3у=10, 1
20х-7у=5. Ответ: (0; 3―)
3
7. Историческая справка.
Уравнения с несколькими переменными, для которых требуется найти решения в натуральных или целых числах, называют диофантовыми уравнениями.В трактате «Арифметика» Диофант излагает остроумные способы решения в натуральных числах самых разнообразных уравнений.
Диофантовые уравнения
| ξ | сигма концевая |
вот этой буквой Диофант и стал обозначать 1-ю степень неизвестного (как наше х).Придумав это, Диофант стал двигаться дальше – квадрат неизвестного он обозначил ∆y. А если числа и неизвестные записаны специальными символами, то нелепо записывать словами действия над ними. И Диофант вместо слова “получится” стал писать значок ﺂ (изос) – равный, вычитание – . А без знака сложения он обходился довольно просто – слагаемые записывал рядом друг с другом. Например:
Придумал Диофант и два основных приема решения уравнений:
– перенос неизвестных;
– приведение подобных.
8. Первичное закрепление нового материала.
№ 1082.
9. Задание на дом: п.44(алгоритм)
№1083 (б, г)
№1084(б, в, г)
10. Итог урока.
Шел мудрец, а навстречу ему три человека, которые везли под горячим солнцем тележки с камнями для строительства. Мудрец остановился и задал каждому по вопросу.
У первого спросил: «Что ты делал целый день?» И тот ответил с ухмылкой, что целый день возил эти проклятые камни.
У второго мудрец спросил: «А что ты делал целый день?», и тот ответил: «А я добросовестно выполнял свою работу».
А третий улыбнулся, лицо его просияло: «А я принимал участие в строительстве Храма!»
Ребята, каждый для себя оцените свою работу.

 Получите свидетельство
Получите свидетельство Вход
Вход












 Открытый урок на тему «Системы линейных уравнений с двумя переменными. Способ сложения». Алгебра 7 класс (585.33 KB)
Открытый урок на тему «Системы линейных уравнений с двумя переменными. Способ сложения». Алгебра 7 класс (585.33 KB)
 0
0 1613
1613 79
79 Нравится
0
Нравится
0


