"Особенность Архимедовых тел"

Государственное бюджетное профессиональное образовательное учреждение

Владимирской области

«Ковровский медицинский колледж имени Е. И. Смирнова»

Дисциплина: «Математика»

Специальность: «Акушерское дело»

Презентация на тему:

«Особенность Архимедовых тел»

Подготовил студент 05 – А группы

Баринова Анна

Проверил преподаватель

Лобанова Е.И.

Ковров 2018 г.

Содержание

• Определение
• История названия
• Классификация
• Свойства
• Построение
• Использованные источники

Определение

В геометрии архимедово тело— это высоко симметричный полуправильный выпуклый многогранник, имеющий в качестве граней два или более типов правильных многоугольников.

История названия

Архимедовы тела названы по имени Архимеда, обсуждавшего их в ныне потерянной работе. Папп Александрийский ссылается на эту работу и утверждает, что Архимед перечислил 13 многогранников. Во времена Возрождения художники и математики ценили чистые формы и заново открыли их все. Эти исследования были почти полностью закончены около 1620 года Иоганном Кеплером, который определил понятия призм, антипризм и невыпуклых тел, известных как тела Кеплера — Пуансо.

Кеплер, возможно, нашёл также удлинённый квадратный гиробикупол — по меньшей мере, он утверждал, что имеется 14 архимедовых тел. Однако его опубликованные перечисления включают только 13 однородных многогранников, и первое ясное утверждение о существовании этой фигуре было сделано в 1905 Дунканом Соммервилем.

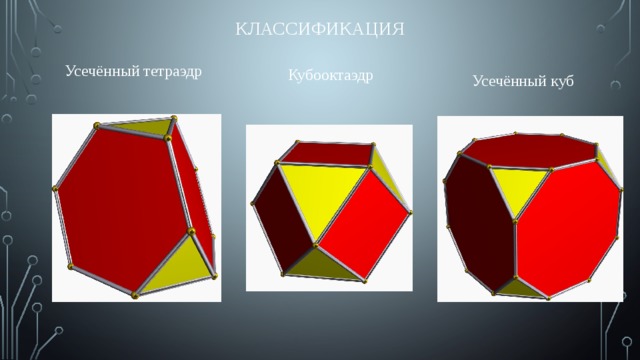
Классификация

Усечённый тетраэдр

Кубооктаэдр

Усечённый куб

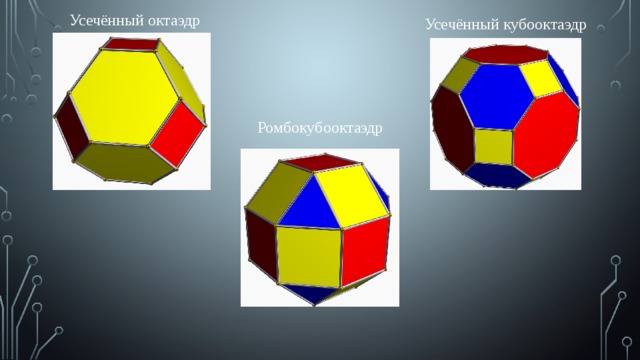
Усечённый октаэдр

Усечённый кубооктаэдр

Ромбокубооктаэдр

Свойства

• Число вершин равно отношению 720° к угловому дефекту при вершине.

• Кубоктаэдр и икосододекаэдр являются рёберно однородными и называются квазиправильными.

• Двойственные многогранники архимедовых тел называются каталановыми телами.

Построение

Различные архимедовы и платоновы тела могут быть получены друг из друга с помощью пригоршни операций. Начиная с платоновых тел можно использовать операцию усечения углов. Для сохранения симметрии усечение делается плоскостью, перпендикулярной прямой, соединяющей угол с центром многоугольника. В зависимости от того, насколько глубоко проводится усечение, получим различные платоновы и архимедовы (и другие) тела. Растяжение или скашивание осуществляется путём движения граней (в направлении) от центра (на одно и то же расстояние, чтобы сохранить симметрию) и созданием, затем, выпуклой оболочки. Расширение с поворотом осуществляется также вращением граней, это ломает прямоугольники, возникающие на местах рёбер, на треугольники. Последнее построение, которое мы здесь приводим, это усечение как углов, так и рёбер. Если игнорировать масштабирование, расширение можно также рассматривать как усечение углов и рёбер, но с определённым отношением между усечениями углов и рёбер.

Список использованной литературы

• https://ru.wikipedia.org
• https://24smi.org
• https://mnogogranniki.ru/