Основные понятия теории вероятности

Основные понятия теории вероятности

Урок 1

Я

СОБЫТИЯ

Тема урока

Примеры:

• Сдача экзамена;
• Выстрел из винтовки;
• Бросание игрального кубика;
• Химический эксперимент и т.д.

• Под событием понимается явление, которое происходит или не происходит
• А так же результат опытов наблюдений и измерений, проводимых людьми

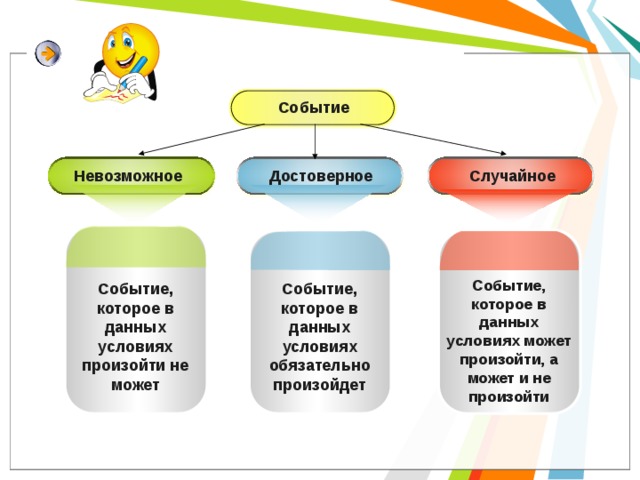
Событие

Случайное

Невозможное

Достоверное

Событие, которое в данных условиях может произойти, а может и не произойти

Событие, которое в данных условиях произойти не может

Событие, которое в данных условиях обязательно произойдет

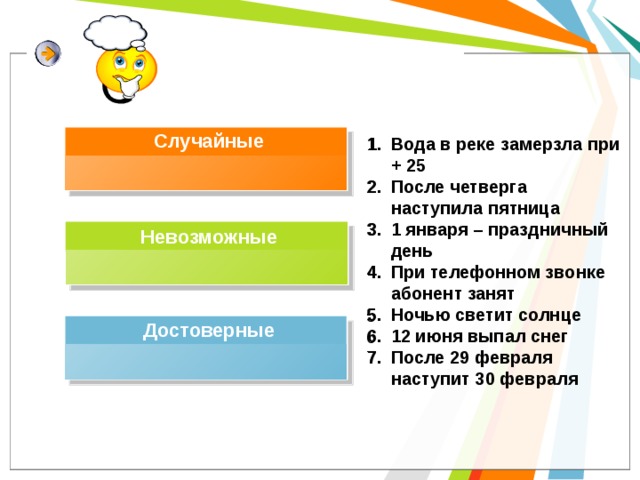
Случайные

• Вода в реке замерзла при + 25
• После четверга наступила пятница
• 1 января – праздничный день
• При телефонном звонке абонент занят
• Ночью светит солнце
• 12 июня выпал снег
• После 29 февраля наступит 30 февраля

1

2

3

Невозможные

4

5

Достоверные

6

7

У математической монеты нет цвета, размера, веса и достоинства. Она не сделана ни из какого материала и не может служить платежным средством.

Contents

• Click to add Text
• Click to add Text
• Click to add Text
• Click to add Text

Название "орел" для обратной стороны (реверса) монеты происходит оттого, что на реверсе российских монет изображен герб Российского государства — двуглавый орел. Впервые орел на монетах появился при великом князе Иване III.

Название "решка" для лицевой стороны (аверса) монеты возникло потому, что рисунок на аверсе российских монет в XVIII-XIX вв. напоминал решетку, на фоне которой был написан номинал монеты (ее достоинство).

• Click to add Text
• Click to add Text
• Click to add Text

Content

Content

Математическая кость не имеет ни цвета, ни размера, ни веса, ни иных материальных качеств. Сумма очков на противоположных гранях правильной кости равна 7.

• Click to add Text
• Click to add Text
• Click to add Text
• Click to add Text

Contents

Об играх с костями животных (игры в "лодыжки", "костыги", "козули") у славян и на языческой Руси свидетельствуют многочисленные археологические находки на обширной территории. Отсюда и русское название игрального кубика — кость.

Игральные кости в виде кубиков находили в Египте (XX в. до н. э.) и в Китае (VI в. до н. э.) при раскопках древних захоронений. Точки на гранях древнеегипетских костей часто изображались в виде птичьего глаза.

• Click to add Text
• Click to add Text
• Click to add Text

Content

Content

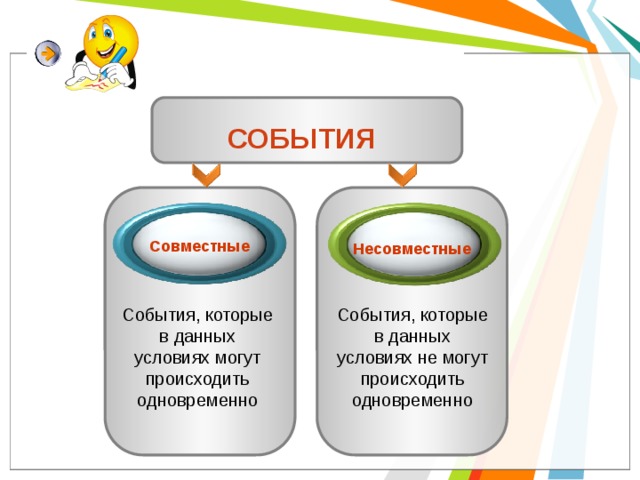
СОБЫТИЯ

Совместные

Несовместные

События, которые в данных условиях могут происходить одновременно

События, которые в данных условиях не могут происходить одновременно

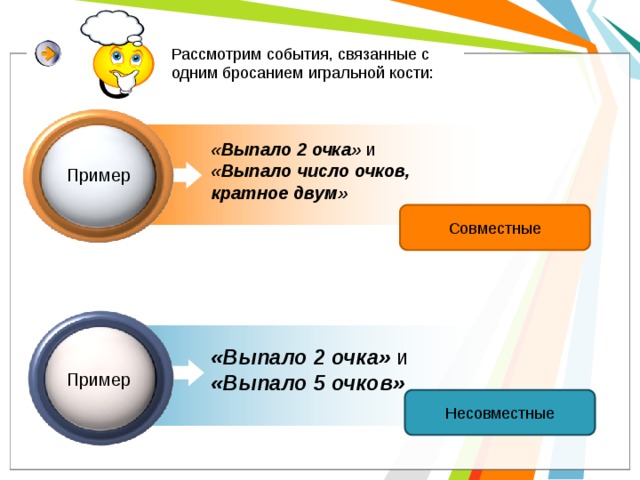
Рассмотрим события, связанные с одним бросанием игральной кости:

«Выпало 2 очка» и

«Выпало число очков, кратное двум»

Пример

Совместные

«Выпало 2 очка» и

«Выпало 5 очков»

Пример

Несовместные

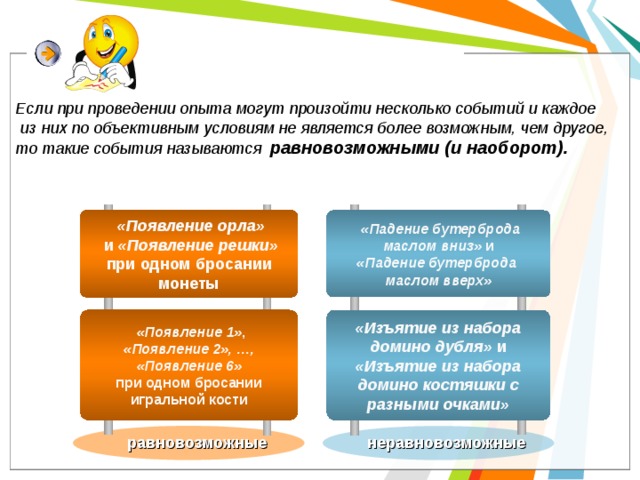
Если при проведении опыта могут произойти несколько событий и каждое

из них по объективным условиям не является более возможным, чем другое,

то такие события называются равновозможными (и наоборот).

«Появление орла»

и «Появление решки»

при одном бросании

монеты

«Падение бутерброда

маслом вниз» и

«Падение бутерброда

маслом вверх»

«Изъятие из набора

«Появление 1» ,

домино дубля» и

«Появление 2», …,

«Появление 6»

«Изъятие из набора

при одном бросании

домино костяшки с

игральной кости

разными очками»

равновозможные

неравновозможные

Задание 1

Укажите, какое из следующих событий достоверное, какое – невозможное и какое случайное:

а) летних каникул не будет ;

б) бутерброд упадет маслом вниз ;

в) учебный год когда-нибудь закончится .

Задание 2

В мешках лежит 10 шаров: 3 синих, 3 белых и 4 красных.

Охарактеризуйте следующее событие:

а) из мешка вынули 4 шара и они все синие;

б) из мешка вынули 4 шара и они все красные;

в) из мешка вынули 4 шара, и все они оказались разного цвета;

г) из мешка вынули 4 шара, и среди них не оказалось шара черного цвета.

Задание 3

Охарактеризуйте события, о которых идет речь в приведенных заданиях как достоверные, невозможные или случайные.

Петя задумал натуральное число. Событие состоит в следующем:

а) задумано четное число;

б) задумано нечетное число;

в) задумано число, не являющееся ни четным, ни нечетным;

г) задумано число, являющееся четным или нечетным.

Задание 4

Петя и Толя сравнивают свои дни рождения. Укажите, какое из следующих событий достоверное, какое – невозможное и какое случайное:

а) их дни рождения не совпадают;

б) их дни рождения совпадают;

в) Петя родился 29 февраля, а Толя – 30 февраля;

г) дни рождения обоих приходятся на праздники – Новый год и День независимости России ;

д) дни рождения в этом году.

Задание 5

Укажите совместность – несовместность случайных событий:

а) (Катя со Славой играли в шахматы)

«Катя выиграла», «Слава проиграл»;

б) (Катя со Славой играли в шахматы)

«Катя проиграла», «Слава проиграл»;

в) «квадратное уравнение имеет два корня»,

«дискриминант больше нуля»;

г) «квадратное уравнение не имеет корней»,

«дискриминант равен нулю».

Задание 6

Из полной колоды в 36 карт наугад вынимается одна карта. Являются ли равновозможными события:

а) «вынуты карта красной масти» и «вынута карта черной масти»;

б) «вынут король» и «вынута дама»;

в ) «вынута карта бубновой масти» и «вынута карта червовой масти»;

г) «вынута карта пиковой масти» и «вынута карта красной масти»;

д) «вынута шестерка треф» и «вынута дама пик»

Итог урока

ВОПРОСЫ:

1

Может ли событие быть одновременно и невозможным и достоверным?

2

Могут ли события быть одновременно и несовместными и совместными?