Основные методы комбинаторики

Тема учебного занятия: Основные понятия комбинаторики

N-факториал

N! – это воспроизведение чисел от 1 до n

Например:

5!=1*2*3*4*5=120

Подсчитать: 2! 3! 4! 5! 6!

Комбинаторика – это раздел математики, посвященный решению задач  выбора и расположения элементов некоторого множества в соответствии с заданными правилами. Комбинаторика изучает комбинации и перестановки предметов, расположение элементов, обладающее заданными свойствами. Обычные вопросы в комбинаторных задачах: Сколькими способами..? Сколько вариантов..?

Основные комбинаторные объекты

• Размещения
• Перестановки
• Сочетания

1.Сколькими способами Дима сможет покрасить пять елок в серебристый, зеленый и синий цвета, если количество краски у него неограничено, а каждую елку он красит только в один цвет?

2. У Димы есть пять шариков: красный, зеленый, желтый, синий и золотой. Сколькими способами он сможет украсить ими пять елок, если на каждую требуется надеть ровно один шарик?

3. А если можно надевать несколько шариков на одну елку (и все шарики должны быть использованы)?

Решение

1) Каждую из пяти елок можно покрасить в один из трех цветов, поэтому всего различных способов существует 3*3*3*3*3 = 35 = 243.

2) На первую елку можно надеть любой из пяти шариков, на вторую елку — любой из оставшихся четырех, и так далее; всего получаем 5*4*3*2*1 = 120 способов.

3) Каждый из шариков можно надеть на любую елку, поэтому в этом случае ответ — 5 5 = 3125.

Размещения

Размещениями  из  n  элементов по  m  элементов называются комбинации, составленные из данных  n элементов по  m  элементов, которые отличаются либо самими элементами, либо порядком элементов.

• Число размещений без повторений  из  n  по  m  ( n  различных элементов) вычисляется по формуле:

• Размещениями с повторениями  из  n  элементов по  m  называются  упорядоченные   m -элементные выборки, в которых элементы могут  повторяться .

Число размещений с повторениями  вычисляется по формуле:

НАПРИМЕР

1. Сколькими способами 4 юноши могут пригласить четырех из шести девушек на танец?

Решение

Два юноши не могут одновременно пригласить одну и ту же девушку. И варианты, при которых одни и те же девушки танцуют с разными юношами считаются, разными, поэтому:

Возможно 360 вариантов.

2. У мальчика остались от набора для настольной игры штампы с цифрами 1, 3 и 7. Он решил с помощью этих штампов нанести на все книги пятизначные номера– составить каталог. Сколько различных пятизначных номеров может составить мальчик?

Решение

Можно  считать,  что  опыт  состоит  в 5-кратном выборе  с

возращением одной из 3 цифр (1, 3, 7). Таким

образом,  число  пятизначных  номеров  определяется  числом  размещений с повторениями из 3 элементов по 5:

Перестановки

Перестановками  из  n  элементов называются размещения из этих  n  элементов по  n  (Перестановки - частный случай размещений).

• Число перестановок без повторений  (n различных элементов) вычисляется по формуле:

• Число перестановок c повторениями  ( k  различных элементов, где элементы могут повторяться m1, m2, …, mk раз и m1 + m2 +… + mk = n, где n - общее количество элементов) вычисляется по формуле:

НАПРИМЕР

1. Сколько различных шестизначных чисел можно составить из цифр 0, 1, 2, 3, 4,5, если цифры в числе не повторяются?

Решение:

1.1) Найдем количество всех перестановок из этих цифр: P6 =6!=720

1.2) 0 не может стоять впереди числа, поэтому от этого числа необходимо отнять количество перестановок, при котором 0 стоит впереди. А это P5 =5!=120.

P6 -P5 =720-120=600. 

2. Сколько разных буквосочетаний можно сделать из букв слова «Миссисипи»?

Решение

Здесь 1 буква «м», 4 буквы «и», 3 буквы «c» и 1 буква «п», всего 9 букв. Следовательно, число перестановок с повторениями равно

Сочетания

Сочетаниями из n элементов по m элементов  называются комбинации, составленные из данных  n  элементов по m  элементов, которые различаются хотя бы одним элементом (отличие сочетаний от размещений в том, что в сочетаниях не учитывается порядок элементов).

• Число сочетаний без повторений  ( n  различных элементов, взятых по  m ) вычисляется по формуле:

• Число сочетаний c повторениями  ( n  элементов, взятых по  m , где элементы в наборе могут повторяться) вычисляется по формуле:

НАПРИМЕР

1. Сколько трехкнопочных комбинаций существует на кодовом замке (все три кнопки нажимаются одновременно), если на нем всего 10 цифр.

Решение

Так как кнопки нажимаются одновременно, то выбор этих трех кнопок – сочетание.

Отсюда возможно

вариантов.

2. В кондитерском магазине продавались 4 сорта пирожных: эклеры, песочные, наполеоны и слоеные. Сколькими способами можно купить 7 пирожных.

Решение

Покупка не зависит от того, в каком порядке укладывают

купленные пирожные в коробку. Покупки будут различными, если

они отличаются количеством купленных пирожных хотя бы

одного сорта. Следовательно, количество различных покупок

равно числу сочетаний четырех видов пирожных по семь –

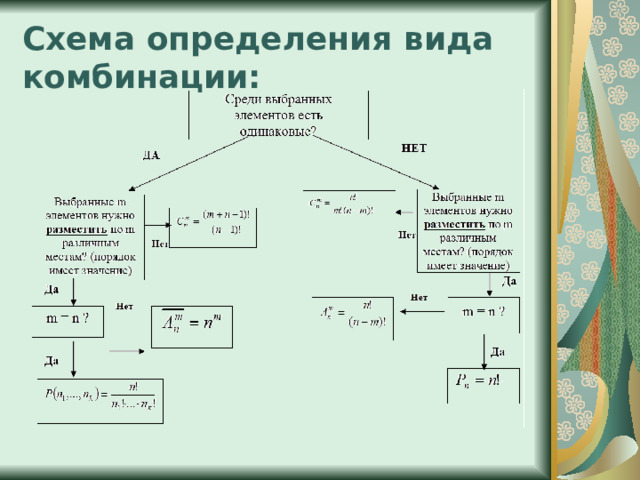
Схема определения вида комбинации:

Решение задач

• У нас есть 9 разных книг из серии “Занимательная математика”. Сколькими способами можно:

1. Расставить их на полке.

2. Подарить три из них победителям школьной олимпиады, занявшим первые три места.

• У бармена есть 6 сортов зеленого чая. Для проведения чайной церемонии требуется подать зеленый чай ровно 3 различных сортов. Сколькими способами бармен может выполнить заказ?
• В группе из 20 студентов надо выбрать 2 представителей для выступления на конференции. Сколькими способами можно это сделать?
• В группе из 20 студентов, среди которых 2 отличника, надо выбрать 4 человека для участия в конференции. Сколькими способами можно выбрать этих четверых, если отличники обязательно должны попасть на конференцию?
• В ящике находится 15 деталей. Сколькими способами можно взять 4 детали?

Домашнее задание

• Сколькими способами из колоды в 36 карт можно выбрать 3 карты?
• В студенческой группе 23 человека. Сколькими способами можно выбрать старосту и его заместителя?
• Сколько существует трёхзначных чисел, которые делятся на 5?
• В лифт 12-этажного дома сели 3 пассажира. Каждый независимо от других с одинаковой вероятностью может выйти на любом (начиная со 2-го) этаже. Сколькими способами:

1)пассажиры могут выйти на одном этаже;  2) два человека могут выйти на одном этаже, а третий – на другом; 3)люди могут выйти на разных этажах; 4) пассажиры могут выйти из лифта?

• Сколько различных слов (не обязательно осмысленных) можно получить перестановкой карточек со следующими буквами: К, О, Л, О, К, О, Л, Ь, Ч, И, К?