МБОУ Новониколаевская сош.
«Организация систематической подготовки учащихся к успешному решению геометрических задач в рамках итоговой государственной аттестации в 9 и 11 классах»
Учитель математики Сигута В. И.
2018 год.
Экзамен по ЕГЭ и ОГЭ по математике при правильной подготовке хорошо может сдать каждый. Формула успеха проста – высокая степень восприимчивости, мотивация и компетентный педагог. В любом случае натаскивание на варианты ЕГЭ и ОГЭ необходимо, но его нужно сочетать с фундаментальной подготовкой, формируя системные знания и навыки.
В ЕГЭ по математике встречаются специфические, каверзные вопросы и задачи. Их часто не может быстро решить даже опытный специалист. Эти задачи на первый взгляд незаметны и их немного, но обязательно включаются разработчиками в ЕГЭ. Однако даже в таких нетиповых заданиях можно выделить шаблоны, что позволяет подготовленному правильным образом ученику уметь распознавать ход мыслей составителя и часто обыгрываемые типы каверзных задач.
Каверзные и специфические задачи составляют только часть так называемой специфики ЕГЭ и ОГЭ по математике. Подготовленность в плане специфики подразумевает знание нюансов и особенностей экзамена. К таким особенностям можно отнести правильность оформления заданий, тактика и стратегия решения в условиях дефицита выделенного времени на экзамене, а также банальная невнимательность. Эти и масса других особенностей и составляют суть специфики. Учитель по математике, хорошо знающий, с чем придется столкнуться школьнику на экзамене, кроме фундамента уделяет большую часть времени на занятии отработке вопросов специфики ЕГЭ и ОГЭ.
Подготовка к сдаче ЕГЭ по математике должна идти через приобретение и освоение конкретных математических знаний. Только это обеспечит выпускнику успешную сдачу экзамена.
В своей работе применяю следующие принципы подготовки к ЕГЭ.
Первый принцип – тематический. Эффективнее выстраивать такую подготовку, соблюдая принцип от простых типовых заданий к сложным.
Второй принцип – логический. На этапе освоения знаний необходимо подбирать материал в виде логически взаимосвязанной системы, где из одного следует другое. На следующих занятиях полученные знания способствуют пониманию нового материала.
Третий принцип – тренировочный. На консультациях учащимся предлагаются тренировочные тесты, выполняя которые дети могут оценить степень подготовленности к экзаменам.
Четвёртый принцип – индивидуальный. На консультациях ученик может не только выполнить тест, но и получить ответы на вопросы, которые вызвали затруднение.
Пятый принцип – временной. Все тренировочные тесты следует проводить с ограничением времени, чтобы учащиеся могли контролировать себя - за какое время сколько заданий они успевают решить.
Шестой принцип – контролирующий. Максимализация нагрузки по содержанию и по времени для всех учащихся одинакова. Это необходимо, поскольку тест по своему назначению ставит всех в равные условия и предполагает объективный контроль результатов.
Следуя этим принципам, формирую у учеников навыки самообразования, критического мышления, самостоятельной работы, самоорганизации и самоконтроля.
Моя цель состоит в том, чтобы помочь каждому школьнику научиться быстро решать задачи, оформлять их чётко и компактно. Развиваю способность мыслить свободно, без страха, творчески. Стараюсь давать возможность каждому школьнику расти настолько, насколько он способен.
Одной из основных причин неуспешной сдачи ЕГЭ являются постоянные изменения в структуре и содержании КИМов как ЕГЭ, так и ОГЭ.
Программы действующих учебников предполагает изучение нового материала даже во втором полугодии 11 класса, в отличие от русского языка, например, изучение которого заканчивается в основной школе. Если отсутствие задач типа А усложняет экзамен для некоторых учащихся, то отдельные виды заданий части В вообще не встречаются в учебниках. Мотивация учащихся, так же как и некоторых родителей, на низком уровне, некоторые предполагают, что им достаточно минимального количества баллов по математике, а при недостаточно серьезном отношении к подготовке в таком случае, проходной балл может быть и не набран. Низкий уровень развития личностных качеств мышления отдельных учащихся также не способствует успешной сдаче ЕГЭ. Следующая причина – это виртуальное пространство бытия школьников. Очевидно, что достаточно большую часть времени школьники средних и особенно старших классов проводят за экранами различных электронных устройств, основная цель которых привлечь внимание, вызвать интерес, заинтриговать. Это достигается за счет наглядности, красочности, динамизма, что, несомненно, является очень увлекательным для подростков. Естественно, что математика, с ее строгой логикой и абстрактным характером изложения (особенно это касается геометрии), не может конкурировать с виртуальной реальностью. Таким образом, мы имеем дело с очень низкой мотивацией к изучению математики даже у школьников, обладающих высоким уровнем интеллекта. Обычно учителя рекомендуют учащимся сайты, где собран теоретический материал, а также сайты, где ученики могут самостоятельно проверить уровень своей подготовки в режиме он-лайн. Но при этом достаточно часто идет реклама сайтов, предлагающих успешно сдать экзамен, зарегистрировавшись в группе в Контакте, например, заплатить и получить ответы накануне экзамена или во время него.
Система работы по подготовке учащихся к итоговой аттестации 9 и 11 классов должна модернизироваться. Этот вопрос относится, прежде всего, к педагогам, не работающим в основной школе и не имеющим достаточного опыта в подготовке к ЕГЭ. Вычислительные умения должны быть хорошо развиты к концу 6 класса, а течение следующего периода обучения лишь совершенствоваться. Вычисления на калькуляторе должны быть сведены к минимуму на всем протяжении обучения в школе и это касается всех предметов школьного курса. Очевидна необходимость получения учащимися как можно большего количества базовых математических знаний уже в основной школе. Реализовывать принцип фундаментальности. Отойти от обучения решения определённых типов и видов математических задач.
Одной из действительно серьезных проблем, особенно при изменении системы оценивания экзаменационных работ ОГЭ, становится преподавание геометрии. В недавнем прошлом экзамен по геометрии сдавали как во время итоговой, так и во время промежуточной аттестации, при этом знания и оценка по геометрии не влияла на экзамен ЕГЭ. Таким образом, возникла необходимость изменения в системе преподавания и отслеживания промежуточных результатов в обучении геометрии в основной школе. Одним из путей реализации поставленной задачи может быть необходимость сдачи устного экзамена на промежуточной аттестации в 7-8 классах.
Анализ пробных тестирований и ЕГЭ показал, что большинство учащихся испытывают существенные затруднения при решении геометрических задач, усвоение которых контролируется в рамках ЕГЭ, не умеют ясно и точно, последовательно и логично выражать свои мысли в письменной форме, не могут аргументировать свою точку зрения. Это говорит о низком уровне сформированности технологической компетенции, самой значимой для практической деятельности.
Необходимо изменить отношение к преподаванию курса геометрии в основной и старшей школах как к предмету, по которому предстоит государственный экзамен за курс средней школы, учащиеся должны не только овладеть теоретическими фактами курса, но и уметь проводить обоснованные решения геометрических задач и математически грамотно их записывать. Создавать положительную мотивацию для усвоения минимума содержания на базовом уровне у всех учащихся, показывать слабым учащимся посильность задач и необходимость их выполнения. Продумывать элементы самоконтроля и научить выпускников оценивать полученные при решении результаты. Проводить не менее 2 – 3 работ, аналогичных ЕГЭ. Предлагать учащимся контрольные и самостоятельные работы по типу заданий приближенных к «формату» ЕГЭ (на 1 – 2 урока). После изучения каждой темы на обобщающем уроке предлагать тестовые задания. На каждом уроке математики систематически повторять изученное ранее параллельно с изучением нового материала. Подготовка к ЕГЭ не должна подменять систематическое изучение математики, а как любая традиционная подготовка к ЕГЭ должна быть обеспечена планомерным повторением, обобщением и систематизацией знаний из различных разделов курса.
Государственная итоговая аттестация по математике позволит выпускникам с разной подготовкой показать свои реальные достижения в овладении различными видами математической деятельности. Чтобы помочь учащимся достичь в этом лучшего результата, учителю необходимо умело, эффективно направлять работу учеников, приводя в систему их знания, организуя тематическое повторение, проводя контроль и коррекцию знаний. Обобщенный план варианта контрольных измерительных материалов для проведения государственной итоговой аттестации (в новой форме) по математике выпускников девятых классов общеобразовательных учреждений содержит шесть задания по геометрии в первой части и три задания во второй. В спецификации КИМ для проведения в 2018 году государственной (итоговой) аттестации (в новой форме) по математике определены основные проверяемые требования к математической подготовке учащихся.
Задания по геометрии экзаменационной работы требуют от учащихся следующих умений:
решать планиметрические задачи на нахождение геометрических величин (длин, углов, площадей);
распознавать геометрические фигуры на плоскости, различать их взаимное расположение, изображать геометрические фигуры;
выполнять чертежи по условию задачи;
выполнять действия с геометрическими фигурами, координатами и векторами;
моделировать реальные ситуации на языке геометрии, исследовать построенные модели с использованием геометрических понятий и теорем;
решать практические задачи, связанные с нахождением геометрических величин;
определять координаты точки плоскости, проводить операции над векторами, вычислять длину и координаты вектора, угол между векторами
В результате изучения геометрии выпускники основной школы должны уметь:
пользоваться языком геометрии для описания предметов окружающего мира;
распознавать геометрические фигуры, различать их взаимное расположение;
изображать геометрические фигуры; выполнять чертежи по условию задач; осуществлять преобразования фигур;
распознавать на чертежах, моделях и в окружающей обстановке основные пространственные тела, изображать их;
в простейших случаях строить сечения и развертки пространственных тел;
проводить операции над векторами, вычислять длину и координаты вектора, угол между векторами;
вычислять значения геометрических величин (длин, углов, площадей, объемов), в том числе: для углов от 0 до 180° определять значения тригонометрических функций по заданным значениям углов; находить значения тригонометрических функций по значению одной из них, находить стороны, углы и площади треугольников, длины ломаных, дуг окружности, площадей основных геометрических фигур и фигур, составленных из них;
решать геометрические задачи, опираясь на изученные свойства фигур и отношений между ними, применяя дополнительные построения, алгебраический и тригонометрический аппарат, идеи симметрии;
проводить доказательные рассуждения при решении задач, используя известные теоремы, обнаруживая возможности для их использования;
решать простейшие планиметрические задачи в пространстве;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
описания реальных ситуаций на языке геометрии;
расчетов, включающих простейшие тригонометрические формулы;
решения геометрических задач с использованием тригонометрии
решения практических задач, связанных с нахождением геометрических величин (используя при необходимости справочники и технические средства);
построений геометрическими инструментами (линейка, угольник, циркуль, транспортир).
Особое внимание стоит обратить на основной список тем по геометрии, подлежащей контролю в конце 9 класса на уроках заключительного повторения, а также при прохождении текущего программного материала:
Отрезок. Луч. Угол.
Треугольники.
Основные геометрические построения.
Параллельные прямые.
Сумма углов треугольника.
Четырехугольники.
Тригонометрические функции острого угла. Теорема Пифагора.
Прямоугольные координаты.
Векторы.
Подобие.
Окружность.
Решение треугольника.
Многоугольники. Длина окружности.
Площадь плоских фигур.
Наличие геометрических задач в КИМ 2018 г. для участников учебно-воспитательного процесса не является неожиданностью, поэтому уже не первый год каждый учитель, исходя из специфики класса, его возможностей, уровня знаний учеников по математике, создает свою модель подготовки учащихся к экзамену, повторяя геометрический материал, обобщая и систематизируя знания выпускников. Успех в решении любой геометрической задачи во многом зависит от теоретической подготовки ученика, от объема накопленных им знаний основных дидактических единиц математики (определение, аксиом, теорем-признаков, теорем-свойств).
С этой точки зрения задание №20 ОГЭ по математике 2018 г.:
Укажите номера верных утверждений.
Диагонали параллелограмма равны.
Два различных диаметра окружности пересекаются в точке, являющейся центром этой окружности.
Сумма углов трапеции равна 3600 .
Площадь прямоугольного треугольника равна произведению катетов.
Синус острого угла прямоугольного треугольника равен отношению противолежащего катета к гипотенузе.
требует от учащихся умения проводить доказательные рассуждения при решении задач, оценивать логическую правильность рассуждений, распознавать ошибочные заключения, заслуживает особого внимания. Выполняя его, выпускник должен, уметь рассуждать методом от противного, владеть способом опровержения неверного утверждения – приведение контрпримера, а самое главное, иметь прочные знания теоретического материала по геометрии за курс основной школы.
В Приложении 1 представлены контрольные вопросы по каждой теме для повторения теоретического материала.
При организации повторения основных теоретических положений геометрии, определенных кодификатором элементов содержания по математике для составления КИМ государственной (итоговой) аттестации выпускников девятых классов общеобразовательных учреждений 2018 года, учителем может быть использовано краткое изложение теории, знание которой можно проверить путем тестирования учащихся (Приложение 2).
Эффективно организовать подготовку к экзамену по математике, определив задолго до него темы, над которыми стоит дополнительно работать. В этом помогут различные диагностические и тренировочные работы.
Организация итогового повторения, к сожалению, не для всех учащихся протекает одинаково результативно. Для ликвидации пробелов в знаниях, при повторной диагностике уровня подготовки выпускников, а также для организации самостоятельной деятельности учащихся, проведения зачетов, совместной работы учащихся в группах и т. д. (на усмотрение учителя), можно использовать дополнительную литературу по математике, цифровые образовательные ресурсы и перечень ресурсов сети Интернет (Приложение 4) полезных в работе учителя математики для подготовки к итоговой аттестации по геометрии.
При подготовке учащихся к решению задач повышенного и высокого уровня сложности (№ 24, 25, 26) учитель не может опираться на случайный набор упражнений. Предлагается система задач, рекомендованная Л. И. Кузнецовой, кандидатом педагогических наук, доцентом кафедры теории и методики обучения математике Нижегородского государственного педагогического университета. Л. И. Кузнецова предлагает тексты задач по темам «Треугольник», «Четырехугольник», «Окружность», «Окружность и треугольник», «Окружность и четырехугольник», «Две окружности» (Приложение 3). Уровень сложности геометрических задач второй части требует от учащихся глубоких и прочных знаний теоретического материала.
Учителю необходимо вносить изменения в поурочное планирование, выделяя резерв времени как во время проведения урока, так и во время обобщающего повторения для закрепления наиболее значимых и сложных тем учебного предмета за курс основной школы.
Подбирать задания с чёткими немногосложными формулировками, включающими понятную для учащихся терминологию, для того чтобы формировать умения кратко, по существу вопроса (устного и письменного) излагать свои знания. Развивать умения формулировать свои мысли, выполнять задания с развёрнутым ответом, комментируя устные ответы обучающихся и ошибки в логике высказываний на ту или иную учебную тему.
Выстроить систему контроля знаний, умений и навыков обучающихся, используя для этого задания, аналогичные заданиям экзаменационных материалов.
Проходить повышение квалификации на курсах повышения квалификации и проблемных семинарах разных уровней методической сети. Заниматься самообразованием по вопросам, связанным с преподаванием школьного курса геометрии и внедрением в практику преподавания предмета современных технологий, направленных на подготовку к тестированию.
В ходе обучения геометрии необходимо обратить самое серьезное внимание на обеспечение усвоения всеми учащимися минимума содержания на базовом уровне, в целях повышения качества освоения обучающимися государственного образовательного стандарта, определенного образовательной программой в рамках учебного года, в соответствии с п. 3 ст. 15 Закона Российской Федерации «Об образовании».
Понятно, что этап формирования базовых умений у менее подготовленных школьников займет больше времени, чем у более подготовленных учащихся. Поэтому в арсенале учителя должны быть средства и методы, позволяющие обеспечить дифференцированный подход к учащимся, предоставить для учащихся со слабой подготовкой возможность более длительной отработки умений в ходе решения простых задач, а для более подготовленных – достаточно быстрый переход к решению задач повышенного уровня. Нужно заметить, что задач первичного закрепления базового материала в учебниках и во многих дидактических материалах очень мало. Поэтому при выборе дидактических пособий (задачников, рабочих тетрадей, карточек и т.п.) следует обращать внимание на наличие, элементарных заданий на закрепление изученного материала. Целесообразно также увеличить число рассматриваемых на уроке задач, где эффективно используется прием устного решения задач по готовым чертежам.
Можно предложить учащимся список задач, которые они должны уметь решать для получения удовлетворительной оценки, например, в качестве заданий для самопроверки достижения обязательной подготовки по теме.
Выполнение заданий повышенного уровня сложности вызывают трудности у значительного числа учащихся, причем, не только у слабоподготовленных, но и у учащихся, имеющих хороший уровень математической подготовки.
В числе причин неуспеха в решении таких задач можно выделить две основные:
во-первых, для решения задач повышенного уровня необходимо использовать имеющиеся знания в измененной учебной ситуации, т. е. в ситуации, не всегда достаточно отрабатываемой на уроках геометрии;
во-вторых, при изучении некоторых разделов курса геометрии особенно проявляется слишком формальное усвоение материала учащимися, такими как «Векторы», «Правильные многоугольники», «Задачи практического содержания».
Таким образом, для того, чтобы быстро и успешно справляться с решением задач повышенного уровня, необходимо выполнение ряда условий. Одним из важнейших условий является уверенное владение свойствами ряда «опорных» геометрических конфигураций, которые часто используются в задачах. Другим, не менее важным, является умение проанализировать предлагаемую в задаче фигуру, распознать в ней опорную конфигурацию и установить связи между ее элементами: их взаимное расположение, метрические соотношения.
При подготовке к итоговой аттестации по математике учитель может использовать цифровые образовательные ресурсы (ЦОР) как на различных этапах урока (проверка домашнего задания, организация фронтального опроса, подготовка учащихся к активному и сознательному усвоению нового материала, объяснение нового материала, усвоение новых знаний, закрепление новых знаний, промежуточный и итоговый контроль знаний умений и навыков, информирование учащихся о домашнем задании, инструктаж по его выполнению, и др.), так и для реализации индивидуальной образовательной траектории обучающегося.
Использование цифровых образовательных ресурсов в обучении геометрии способствует не только повышению интереса у школьников к учебному предмету, но и развитию аналитических, проекционных и конструкторских способностей; развитию психических функций (логическое мышление, память, внимание, воображение, восприятие, др.); формированию коммуникативных навыков и готовности к самостоятельной научно-исследовательской работе.
К сожалению, в традициях устного экзамена по геометрии за курс основной школы существовала возможность получения удовлетворительной отметки лишь по результатам выполнения теоретической части билета при отсутствии или неправильном выполнении его практической части.
В условиях прохождения итоговой аттестации подобная практика исключена. Поэтому учащиеся должны быть заранее осведомлены о том, что они могут быть положительно аттестованы только в том случае, если научатся самостоятельно решать задачи, овладение которыми показывает усвоение материала на базовом уровне. Желательно при изучении каждой темы ознакомить учащихся с требованиями Стандарта к уровню подготовки выпускников.
Формирование умений решать задачи базового уровня – непременное условие для усвоения геометрии на любом уровне. Это обязательная часть учебного процесса, недооценивать которую нельзя. Только после этого этапа можно переходить к формированию умений решать геометрические задачи повышенного и высокого уровней.
В этой связи, отметим, что успешное выполнение вариантов государственной итоговой аттестации всецело зависит от полноценного и глубокого изучения всего программного материала по действующим учебникам
Таким образом, подготовка к государственной итоговой аттестации по математике должна быть обеспечена также качественным изучением предмета геометрии, продуманным текущим повторением, и, наконец, обязательным обобщением, систематизацией знаний из различных разделов курса геометрии.
Приложение 1
Контрольные вопросы для повторения теоретического материала
Тема: « Отрезок. Луч. Угол»
Объясните, что такое отрезок с концами А и В. Как он обозначается?
Какие отрезки называются равными?
Объясните, как сравнить два отрезка.
Какая точка называется серединой отрезка?
Объясните, что такое луч. Как обозначаются лучи? Какие лучи называются дополнительными?
Какая фигура называется углом? Объясните, что такое вершины и стороны угла. Как обозначается угол?
Какой угол называется развернутым?
Какие углы считаются равными?
Объясните, как сравнить два угла?
Какой луч называется биссектрисой угла?
Точка С делит отрезок АВ на два отрезка. Как найти длину отрезка АВ, если известные длины отрезков АС и СВ?
Что такое градусная мера?
Луч ОС делит угол АОВ на два угла. Как найти градусную меру углов АОВ, если известны градусные меры углов АОС и СОВ?
Какой угол называется острым? Прямым? Тупым?
Какие углы называются смежными?
Докажите, что сумма смежных углов равна 180о.
Какие углы называются вертикальными? Докажите, что вертикальные углы равны.
Какие углы называются перпендикулярными? Что называется серединным перпендикуляром к отрезку?
Объясните, какой отрезок называется перпендикуляром, проведенным из данной точке к данной прямой.
Сформулируйте теорему о перпендикуляре, проведенном из данной точки к данной прямой.
Тема: « Треугольники».
Какая фигура называется треугольником? Начертите треугольник и покажите его стороны, вершины и углы. Что такое периметр треугольника?
Какой угол называется внешним углом треугольника?
Какой отрезок называется биссектрисой треугольника?
Какой отрезок называется медианой треугольника? Сколько медиан имеет треугольник?
Какой отрезок называется высотой треугольника? Сколько высот имеет треугольник?
Какой треугольник называется остроугольный? Какой треугольник называется тупоугольным?
Какой треугольник называется прямоугольным? Как называются стороны прямоугольного треугольника?
Какой треугольник называется равнобедренным? Как называются его стороны?
Какой треугольник называется равносторонним?
Какие треугольники называются равными?
Сформулируйте и докажите первый признак равенства треугольников.
Сформулируйте второй признак равенства треугольников.
Сформулируйте теорему о сумме двух внутренних углов треугольника.
Сформулируйте теорему о соотношении внешнего угла треугольника с его внутренним углом, не смежным с этим внешним.
Докажите, что углы при основании равнобедренного треугольника равны.
Сформулируйте теорему о биссектрисе равнобедренного треугольника, проведенной к основанию.
Сформулируйте третий признак равенства треугольников.
Тема: «Основные геометрические построения».
Какая геометрическая фигура называется окружностью? Что называется радиусом окружности?
Что такое секущая, хорда окружности? Какая хорда называется диаметром?
Объясните, как построить треугольник по трём сторонам?
Объясните, как отложить от данного луча угол, равный данному углу.
Объясните, как построить биссектрису данного угла.
Объясните, как провести серединный перпендикуляр к данному отрезку.
Объясните, как разделить данный отрезок пополам.
Объясните, как через данную точку провести прямую, перпендикулярную прямую данной прямой.
Тема: «Параллельные прямые».
Какие прямые называются параллельными?
Что такое секущая по отношению к двум прямым?
Какие углы называются накрест лежащими?
Какие углы называются соответственными?
Объясните, какие углы называются односторонними.
Сформулируйте признаки параллельности прямых.
Каково взаимное расположение двух прямых, перпендикулярных
Одной и той же прямой?
Сформулируйте аксиому о параллельных прямых.
Можно ли утверждать, что две различные прямые, параллельные
третьей, параллельны между собой?
Сформулируйте теорему об углах, образованных двумя параллельными прямыми секущей.
Тема: «Сумма углов треугольника».
Докажите теорему о сумме углов треугольника.
Чему равна сумма острых углов прямоугольного треугольника?
Чему равен каждый острый угол равнобедренного прямоугольного треугольника?
Чему равны углы равностороннего треугольника?
Какими могут быть углы в любом треугольнике?
Докажите, что внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним.
Докажите, что в треугольнике против большей стороны лежит больший угол. Сформулируйте обратную теорему.
Сформулируйте признак равнобедренного треугольника
Что такое равенство треугольников?
Что называется расстоянием от точки до прямой?
Сформулируйте два признака равенства прямоугольных треугольников, непосредственно следующих из первого и второго признаков равенства треугольников.
Докажите признак равенства прямоугольных треугольников по гипотенузе и острому углу.
Сформулируйте признак равенства прямоугольных треугольных треугольников по гипотенузе и катету.
Тема: «Четырехугольники».
1. Какая фигура называется четырехугольником?
2. Какие вершины четырехугольника называются соседними, какие противолежащими?
3. Что такое диагонали четырехугольника?
4. Какие стороны четырехугольника называются смежными? Какие называются противоположными?
5. Что такое параллелограмм?
6. Сформулируйте и докажите свойство сторон и углов параллелограмма.
7. Что называется расстоянием между параллельными прямыми?
8. Сформулируйте свойства параллелограмма.
9. Сформулируйте признаки параллелограмма.
10. Какой параллелограмм называется прямоугольником?
11. Докажите, что диагонали прямоугольника равны.
12. Сформулируйте признак прямоугольника .
13. Какой параллелограмм называется ромбом? Докажите, что диагонали ромба взаимно перпендикулярны и делят углы пополам.
14. Какой прямоугольник называется квадратом? Сформулируйте основные свойства квадрата.
15. Сформулируйте и докажите теорему Фалеса.
16. Какой отрезок называется средней линией треугольника?
Сформулируйте теорему о средней линии треугольника.
17. Какой четырёхугольник называется трапецией?
18. Как называются стороны трапеции?
19. Какая трапеция называется равнобедренной, какая – прямоугольной?
20. Какой отрезок называется средней линией трапеции?
Сформулируйте теорему о средней линии трапеции.
21. Какие две точки называются симметричными относительно данной точки?
22. Какая фигура называется симметричной относительно данной точки?
23. Какие две точки называются симметричными относительно данной прямой?
24. Какая фигура называется симметричной относительно данной прямой? Приведите примеры фигур, обладающих: а) центральной симметрией; б) осевой симметрией; в) и центральной и осевой симметрией.
25. Что называется отношением двух отрезков? В каком случае отрезки AB и CD пропорциональны отрезкам A1 B1 и C1 D1?
Тема: «Тригонометрические функции острого угла. Теорема Пифагора».
Что называется косинусом, синусом и тангенсом острого угла прямоугольного треугольника?
Сформулируйте и докажите теорему Пифагора.
Приведите основные тригонометрические тождества.
Чему равны значения синуса, косинуса и тангенса для углов 30о, 45о, 60о?
Как выражается катет прямоугольного треугольника через гипотенузу и острый угол?
Как выражается катет прямоугольного треугольника через другой катет и острый угол?
В чем состоит решение прямоугольного треугольника?
Каковы основные случаи решения прямоугольного треугольника?
Тема: «Прямоугольные координаты».
Что называется координатной осью?
Что называется координатной точки, лежащей на оси Ох?
Объясните, как вводится прямоугольная система координат на плоскости.
Приведите формулу для вычисления расстояния между двумя точками по их координатам.
Напишите формулы координат середины отрезка.
Дайте определение синуса, косинуса и тангенса для любого угла от 0 до 180о.
Докажите, что для любого угла α, 000 , sin(1800 – α) =s in α, cos (1800 – α)= – cos α.
Тема: «Векторы».
Что называется вектором?
Что называется абсолютной величиной вектора?
Какой вектор называется единичным?
Какой вектор называется нулевым?
Какие векторы называются коллинеарными?
Дайте определение равных векторов.
Какие векторы называются противоположными?
Какой вектор называется суммой двух векторов ?
Какой вектор называется разностью двух векторов?
Какой вектор называется произведением данного вектора и данного действительного числа?
В чем состоит разложение вектора по осям Оx и Оy?
Что называется координатами вектора?
Сформулируйте правила нахождения координат суммы и разности вектора, а также произведения вектора на число по заданным координатам векторов.
Что такое скалярное произведение двух векторов?
Как определяется угол между векторами? Чему равно скалярное произведение двух векторов?
Тема: «Подобие».
Какие треугольники называются подобными?
Сформулируйте и докажите первый признак подобия треугольников.
Сформулируйте второй признак подобия треугольников.
Сформулируйте третий признак подобия треугольников.
Какие четыре точки называются замечательными точками треугольника?
Какие две фигуры называются подобными?
Что называется коэффициентом подобия?
Что называется гомотетией?
Какие фигуры называются гомотетичными?
Что такое параллельный перенос?
Тема: «Окружность».
Какая прямая называется касательной к окружности?
Что значит: окружности касаются в данной точке?
Какое касание окружностей называется внутренним, какое – внешним?
Что называется плоским углом?
Какой угол называется центральным?
Какой угол называется вписанным в окружность?
Докажите, что вписанный в окружность угол равен половине соответствующего центрального угла.
Какая окружность называется вписанной в треугольник?
Докажите, что центр окружности, вписанной в треугольник, является точкой пересечения его биссектрис.
Какая окружность называется описанной около треугольника?
Где лежит центр окружности, описанной около треугольника?
Тема: «Решение треугольника».
Сформулируйте и докажите теорему синусов.
Сформулируйте теорему косинусов.
В чём состоит решение треугольников?
Каковы основные случаи решения треугольников?
Тема: «Многоугольники. Длина окружности».
Что такое ломаная?
Что такое многоугольник?
Какой многоугольник называется выпуклым?
Чему равна сумма углов выпуклого n-угольника?
Какой многоугольник называется вписанным в окружность?
Какой многоугольник называется описанным около окружности?
Какой многоугольник называется правильным?
Приведите формулы для радиусов вписанной и описанной окружностей правильного n-угольника.
Найдите радиусы вписанной и описанной окружностей для правильного треугольника, четырехугольника (квадрата), шестиугольника.
По какой формуле вычисляется длина окружности?
По какой формуле вычисляется длина дуги окружности?
Что такое радианная мера угла?
Чему равны радианные меры развернутого и прямого углов?
Тема: «Площадь плоских фигур».
Сформулируйте свойства площади для простых фигур.
Докажите теорему о вычислении площади параллелограмма.
Докажите теорему о вычислении площади треугольника.
Какие вам известны формулы для площади прямоугольного треугольника и ромба?
Докажите теорему о площади трапеции.
Сформулируйте теорему о площади правильного многоугольника.
Чему равна площадь круга?
Чему равна площадь сектора?
Приложение 2
Тестирование учащихся при проверке теории
Заполните пропуски так, чтобы утверждение было верным
1.Через любые ……точки проходит прямая, и притом …………..
2.Две прямые либо имеют …………общую точку, либо не имеют ……..точек.
3.Если углы вертикальные, то ..…………………………. .
4.Сумма смежных углов равна ………… .
5.Из точки, не лежащей на прямой, … …. перпендикуляр к этой прямой, и притом ………
6.Если две параллельные прямые пересечены секущей, то:
1)…………………….………………………. углы равны;
2). …………………..……………… углы равны;
3). ……………………..…………………………….. равна 180°.
7.Если прямая пересекает одну из двух параллельных прямых, то она……. . 8.Если прямая перпендикулярна к одной из двух параллельных прямых, то она ………..………
9. Если две прямые параллельны третьей прямой, то они…………………….. 10.Если две прямые, перпендикулярны к третьей, то они…………….
11.Две прямые параллельны, если при пересечении этих прямых секущей
1). ……………………………………….…………….. углы равны,
2). …………..……..………………..…………………. углы равны,
3). ……………….………………..…………………… углов равна 180°.
12.Перпендикуляр, проведенный из точки к прямой, ……любой наклонной, проведенной из этой точки к прямой.
13.Каждая точка биссектрисы неразвернутого угла равноудалена от ………. 14.Каждая точка серединного перпендикуляра к отрезку равноудалена от…… 15.Сумма углов треугольника равна …………………
16.Средняя линия треугольника ……одной из его сторон и равна ……
17.Внешний угол треугольника равен ….… двух углов треугольника
18.Каждая сторона треугольника ……суммы двух других сторон.
19.В треугольнике:
1) против большей стороны лежит ………………..угол;
2) против большего угла лежит ………………….. сторона.
20. Все медианы треугольника пересекаются в ……, которая делит каждую
медиану в отношении ………, считая от ……………..….
21. Все биссектрисы треугольника пересекаются в ……и каждая из них делит
противоположную сторону на отрезки, ……сторонам треугольника.
22.Все высоты треугольника пересекаются в ………………………...
23.Все серединные перпендикуляры к сторонам треугольника пересекаются в ……………………….
24.В равнобедренном треугольнике:
1) углы …………….......... равны;
2) биссектриса, медиана, высота, проведенные ….……., совпадают.
25.Треугольник является равнобедренным, если:
1)……………………… равны;
2) биссектриса является …………………..;
3) медиана является ………………………;
4) биссектриса является …………………...
26. В равностороннем треугольнике биссектрисы, медианы и высоты пересекаются в ………………...…
27.Треугольник с тремя равными углами является ………………………..
Приложение 3
Тексты задач по основным темам геометрии
Треугольник
Основание АС равнобедренного треугольника АВС равно 32, а боковые стороны 20.Из вершины B проведен перпендикуляр к боковой стороне до пересечения с прямой АС в точке D. Найдите DA и DC.
Найдите площадь равнобедренного треугольника, если его основание равно а, а длина высоты, проведенной к основанию, равна длине отрезка, соединяющего середины основания и боковой стороны.
Стороны АВ, BC и АС треугольника АВС равны соответственно
13 см, 15 см и 14 см. Вычислите площадь треугольника, заключенного между высотой и биссектрисой, проведенными из вершины В.
В равнобедренном треугольнике АВС с основанием АВ высота СН равна половине биссектрисы AD. Найдите углы треугольника АВС.
Высоты АН и ВК равнобедренного треугольника АВС с основанием BC пересекаются в точке O, АН = BC = 8
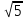 . Найдите площадь треугольника АВО.
. Найдите площадь треугольника АВО. В треугольнике АВС точка E – середина биссектрисы CM. В каком отношении прямая АЕ делит площадь треугольника АВС, если известно, что отношение СА:CВ = p: q?
Площадь треугольника АВС равна 80. Биссектриса BL пересекает медиану СК в точке E, при этом AL:CL = 2:3. Найдите площадь четырехугольника ALEK.
Площадь треугольника ABC равна 120, точка D лежит на отрезке BC так, что BD:CD = 1:2, биссектриса BK пересекает прямую AD в точке L. Найдите площадь четырехугольника KLDC, если AK: KC = 3:1.
На стороне AC треугольника ABC взята точка E такая, что EC = AB. Пусть K − середина BC, M − середина AE. Найдите градусную меру угла BAC, если ∠ KME = 20°.
Четырехугольник
На сторонах AB, BC и AC треугольника ABC взяты точки K, L и T соответственно, причем
 . Найдите площадь треугольника ABC, если KBLT−параллелограмм с площадью, равной 7.
. Найдите площадь треугольника ABC, если KBLT−параллелограмм с площадью, равной 7. В параллелограмме ABCD углы B и D – острые. Известно, что BK – биссектриса угла B, CM – биссектриса угла C, а точки K и M лежат на отрезке AD. Найдите, как площадь трапеции BCMK относится к площади ABCD, если BC =10, AB = 3.
Прямая, проходящая через вершину A квадрата ABCD, пересекает сторону CD и точке M и продолжение стороны BC в точке N. Найдите сторону квадрата, если AM = 5, MN = 3.
В треугольник ABC со сторонами AB = 10, BC = 7, AC = 15 вписан квадрат, две вершины которого лежат на стороне AC, одна – на стороне AB и одна − на стороне BC. Через середину D стороны AC и центр квадрата проведена прямая, которая пересекается с высотой BH треугольника ABC в точке M. Найдите площадь треугольника DMC.
Диагонали АС и BD трапеции ABCD пересекаются в точке О. Площади треугольников AOD и BOC равны соответственно 25см2 и 16см2. Найдите площадь трапеции.
Дана трапеция ABCD с основаниями AD = а и BC = b. Точки М и N лежат на сторонах АВ и CD соответственно, причем отрезок MN параллелен основаниям трапеции. Диагональ АС пересекает этот отрезок в точке О. Найдите MN, если известно, что площади треугольников АМО и CNO равны.
Длины диагоналей трапеции равны 9см и 12см, а длина ее средней линии равна 7,5 см. Найдите площадь трапеции.
Углы при одном из оснований трапеции равны 44° и 46°, а отрезки, соединяющие середины противоположных сторон трапеции, равны 44 см и 46 см. Найдите основания трапеции.
Найдите площадь трапеции, если ее диагонали равны 3 и 5, а отрезок, соединяющий середины оснований, равен 2.
Окружность
Окружность проходит через середины гипотенузы АВ и катета BC прямоугольного треугольника АВС и касается катета АС. В каком отношении точка касания делит катет АС?
Длина катета АС прямоугольного треугольника АВС равна 8 см. Окружность с диаметром АС пересекает гипотенузу АВ в точке М. Найдите площадь треугольника АВС, если известно, что АМ:MВ = 16:9.
Длина медианы CM треугольника АВС равна 5 см. Окружность с диаметром СМ пересекает стороны АС и BC в их серединах. Найдите периметр треугольника АВС, если его площадь равна 24см2.
В окружности с центром O проведены две хорды MN и PQ, при этом ᴗ PQ + ᴗ MN = 180°. На хорду MN опущен перпендикуляр OH, на хорду PQ опущен перпендикуляр AH1. Докажите, что PQ = 2OH.
Окружность и треугольник
Треугольник ABC, в котором ∠ A = 45°, AB = AC
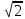 , вписан в окружность радиуса 4, а хорда этой окружности, проходящая через вершину B и центр вписанной в этот треугольник окружности, пересекает сторону AC в точке M. Найдите площадь треугольника AMB.
, вписан в окружность радиуса 4, а хорда этой окружности, проходящая через вершину B и центр вписанной в этот треугольник окружности, пересекает сторону AC в точке M. Найдите площадь треугольника AMB.В треугольнике ABC биссектриса угла A делит высоту, проведенную из вершины В, в отношении 13:12, считая от точки В. Найдите длину стороны BC треугольника, если радиус описанной около него окружности равен 26 см.
Через точку D основания АВ равнобедренного треугольника АВС проведена прямая CD, пересекающая описанную около треугольника АВС окружность в точке Е. Найдите АС, если СЕ = 3 и DE= DC.
В параллелограмме ABCD длина диагонали BD равна 5 см, угол C равен 60°. Окружность, описанная около треугольника ABD, касается прямой CD. Найдите периметр параллелограмма.
В треугольнике KLM угол L тупой, а сторона KM = 6. Найдите радиус описанной около треугольника KLM окружности, если известно, что на этой окружности лежит центр окружности, проходящей через вершины K,M и точку пересечения высот треугольника KLM.
Площадь ромба ABCD равна 18. В треугольник ABD вписана окружность, которая касается стороны АВ в точке К. Через точку К проведена прямая, параллельная диагонали АС и отсекающая от ромба треугольник площади 1. Найдите синус угла BAC.
Прямоугольный треугольник ABC разделен высотой CD, проведенной к гипотенузе, на два треугольника BCD и ACD. Радиусы окружностей, вписанных в эти треугольники, равны 4 и 3 соответственно. Найдите радиус окружности, вписанной в треугольник ABC.
Окружность и четырехугольник
Вершины четырехугольника ABCD делят длину описанной около него окружности в отношении АВ:BC: СD: СА = 2:17:4:13. Найдите площадь четырехугольника, если АС = 8 см, BD = 9 см.
Четырехугольник ABCD, диагонали которого взаимно перпендикулярны, вписан в окружность. Перпендикуляры, опущенные и на сторону AD из вершин B и C, пересекают диагонали AC и BD в точках E и F соответственно. Известно, что BC = 1. Найдите EF.
Хорда окружности удалена от центра на расстояние h. В каждый из сегментов, стягиваемых хордой, вписан квадрат так, что две соседние вершины квадрата лежат на дуге, две другие – на хорде. Чему равна разность длин сторон квадрата?
Около окружности описана трапеция ABCD, боковая сторона AB перпендикулярна основаниям, M – точка пересечения диагоналей трапеции. Площадь треугольника CMD равна S. Найдите радиус окружности.
Трапеция вписана в окружность, диаметр которой является основанием трапеции и равен 2
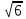 . Найдите второе основание трапеции, если одна из боковых ее сторон равна 3.
. Найдите второе основание трапеции, если одна из боковых ее сторон равна 3.Около окружности радиуса 3 описана равнобедренная трапеция. Площадь четырехугольника, вершинами которого являются точки касания окружности и трапеции, равна 12. Найдите площадь трапеции.
Две окружности
К двум непересекающимся окружностям проведены две общие внешние касательные и общая внутренняя касательная. Докажите, что отрезок внутренней касательной, заключенный между внешними касательными, равен отрезку внешней касательной, заключенному между точками касания.
Окружность радиуса 6 см касается внешним образом второй окружности в точке С. Прямая, проходящая через точку С, пересекает первую окружность в точке А, а вторую окружность − в точке В. Найдите радиус второй окружности, если АС = 4 см, BC = 6 см.
Две окружности с радиусами 5 и 3 касаются в точке О. Их общая касательная, проходящая через точку О, пересекает внешние касательные этих окружностей в точках А и B соответственно. Найдите АВ.
Приложение 4
Цифровые образовательные ресурсы
1) Учебники геометрии, к которым разработаны наборы цифровых образовательных ресурсов (ЦОР), расширяющие учебники/УМК – это представленные в цифровой форме фотографии, видеофрагменты, статические и динамические модели, объекты виртуальной реальности и интерактивного моделирования, картографические материалы, звукозаписи, символьные объекты и деловая графика, текстовые документы и иные учебные материалы, необходимые для организации учебного процесса.
Атанасян Л. С. и др. Геометрия, 7—9. — М.: Просвещение, 2010.
2) Информационные источники сложной структуры (ИИСС) – это цифровой образовательный ресурс, основанный на структурированных цифровых материалах (текстах, видеоизображениях, аудиозаписях, фотоизображениях, интерактивных моделях и т.п.) с соответствующим учебно-методическим сопровождением, поддерживающий деятельность учащихся и учителя по одной или нескольким темам (разделам) предметной области или обеспечивающий один или несколько видов учебной деятельности в рамках некоторой предметной области.
«Геометрический планшет для построения на плоскости»
Булычев В., Емельянов Л. ооо «дос»,2009.
Этот ресурс предназначен для использования в рамках курса планиметрии 7—9-х классов основной школы и 10—11-х классов профильной школы, а также для проведения математических кружков и факультативов. Регулярное применение планшета призвано сделать изучение геометрии более осознанным и интересным, раскрыть творческие способности учащихся, помочь в нахождении закономерности в геометрических конструкциях, дать возможность не только экспериментально проверять геометрические факты и гипотезы, но и выдвигать собственные гипотезы на основании эксперимента. Этот ресурс включен в Единую коллекцию цифровых образовательных ресурсов, можно скачать с http://school-collection.edu.ru/.
«Конструктивные геометрические задания»
Дубровский В., Егоров Ю., Ерганжиева Л. М.:ЗАО «1С»,2009.
Этот ресурс представляет собой подборку 200 задач с проверкой их решений и представлением авторских решений в нескольких вариантах, выполненных в виде интерактивных моделей. Ресурс можно эффективно использовать для подготовки к итоговой аттестации по геометрии. Этот ресурс включен в Единую коллекцию цифровых образовательных ресурсов, можно скачать с http://school-collection.edu.ru/.
«Школьный математический словарь-справочник»
Дубровский В., Раббот Ж. М.: ЗАО «1С»,2009.
Этот ресурс представляет собой гипертекстовую справочную систему, содержащую определения и разъяснения основных понятий школьного курса математики, описания их взаимосвязей, разбор основных методов и алгоритмов решения типовых задач и иллюстраций к ним. Словарные статьи, сгруппированные в алфавитном порядке, содержат и понятия, и конкретные примеры в виде графиков и моделей. Этот ресурс включен в Единую коллекцию цифровых образовательных ресурсов, можно скачать с http://school-collection.edu.ru/.
«Дидактические игры на уроке математики»
Башмаков М., Дубровский В., Поздняков С. М.: ЗАО «1С»,2009.
Этот ресурс предназначен для введения дидактической игры как одного из основных средств решения учебных задач в преподавании математики в 5-6-х классах, алгебры и геометрии — в 7-9-х классах. Активное использование на уроке игровых ситуаций позволяет повысить мотивацию учебной работы, включить в работу недостаточно подготовленных учащихся, индивидуализировать процесс обучения, развивать коммуникативные способности и коммуникативные навыки. Этот ресурс включен в Единую коллекцию цифровых образовательных ресурсов, можно скачать с http://school-collection.edu.ru/.
Виртуальная школа Кирилла и Мефодия «Уроки геометрии 7 класс», «Уроки геометрии 8 класс», «Уроки геометрии 9 класс» .
М.:ОАО «Кирилл и Мефодий,2008..
Этот ресурс предназначен для использования в рамках курса планиметрии 7—9-х классов основной школы, а также для проведения математических кружков и факультативов. Этот комплект позволяет осуществить
получение основополагающих знаний по изучаемому курсу;
дополнительные материалы – энциклопедические статьи;
отработку умений и навыков с помощью интерактивных тренажеров;
проверку знаний по отдельным частям темы, целиком по теме;
обучение самостоятельной работе с материалом;
выявление слабых мест в понимании предмета и стимулирование к более глубокому его изучению;
подготовку к экзамену.
3) Инновационные учебно-методические комплексы (ИУМК) – это полный набор средств обучения, необходимых для организации и проведения учебного процесса, который за счет активного использования современных педагогических и информационно-коммуникационных технологий должен обеспечивать достижение образовательных результатов, необходимых для подготовки учащихся к жизни в информационном обществе, включая:
• фундаментальность общеобразовательной подготовки;
• способность учиться;
• коммуникабельность, умение работать в коллективе;
• способность самостоятельно мыслить и действовать;
• способность решать нетрадиционные задачи, используя приобретенные предметные, интеллектуальные и общие знания, умения и навыки.
«Геометрия. 9 класс. Динамическая геометрия»
Вернер А., Никитин А., Поздняков С. и др. М.: Просвещение,2009.
По сравнению с классическими подходами к преподаванию геометрии, в данном ИУМК ставится задача познакомить выпускников основной школы с более современными методами геометрии: векторным методом, методом координат и методом преобразований. При этом ключевой становится тема «Преобразования»: появление в школе компьютерной техники позволяет изучать эту тему на новом, динамическом уровне, невозможном ранее при статичных иллюстрациях в школьных учебниках и учебных пособиях. ИУМК предоставляет учителю и ученику возможность дифференцированного подхода к изучению геометрии: от опытной, наглядной геометрии до углубленного уровня путем рассмотрения более серьезных вопросов, касающихся тонкостей теории. В ИУМК реализовано три уровня сложности: общеобразовательный, расширенный и углубленный. Этот ресурс включен в Единую коллекцию цифровых образовательных ресурсов, можно скачать с http://school-collection.edu.ru/.
Далее приведены ссылки на ресурсы Интернет, полезные в работе учителя математики, позволяющие использовать материалы при подготовке учащихся к государственной итоговой аттестации:
Российский портал открытого образования http://www.openet.edu.ru/
Федеральный институт педагогических измерений http://www.fipi.ru/
Портал информационной поддержки Единого государственного экзамена http://www.ege.edu.ru/
Московский центр непрерывного математического образования
http://www.mccme.ru/
Сеть творческих учителей. Сообщество учителей математики
http://www.it-n.ru/communities.aspx?cat_no=4510&tmpl=com
Открытый класс. Сообщество «Мир математики» http://www.openclass.ru/node/2367
Газета "Математика" Издательского дома "Первое сентября" http://1september.ru/
Фестиваль педагогических идей «Открытый урок» («Первое сентября») http://festival.1september.ru/
Единая коллекция цифровых образовательных ресурсов http://school-collection.edu.ru/
Сайт УМК Смирновых по геометрии для 7-11 классов http://geometry2006.narod.ru/
Геометрия – электронный урок «Многоугольники» – http://www.geometry-exe.h17.ru/
Математика в Открытом колледже http://www.mathematics.ru/
Интернет-поддержка учителей математики http://www.math.ru/
AIlmath.ru — вся математика в одном месте http://www.allmath.ru/
Exponenta.ru: образовательный математический сайт http://www.exponenta.ru/
Вся элементарная математика: Средняя математическая интернет-школа http://www.bymath.net/
Геометрический портал http://www.neive.by.ru/
Задачи по геометрии: информационно-поисковая система http://zadachi.mccme.ru/
Математические этюды http://www.etudes.ru/
Математические олимпиады и олимпиадные задачи http://www.zaba.ru/
Международный математический конкурс "Кенгуру" http://www.kenguru.sp.ru/
Методика преподавания математики http://methmath.chat.ru/
Московская математическая олимпиада школьников http://olympiads.mccme.ru/mmo/
Сайт элементарной математики Дмитрия Гущина http://www.mathnet.spb.ru/
Сайт Издательства «Просвещение» http://www.prosv.ru
Сайт Издательства «Мнемозина» http://www.mnemozina.ru
Сайт Издательства «Дрофа» http://www.drofa.ru
Сайт Издательства «Вентана-Граф» http://www.vgf.ru
Сайт Издательства «Интеллект-Центр» http://www.intellectcentere.ru
Интернет-магазин ООО «Топ-Книга» http://top-kniga.ru

 Получите свидетельство
Получите свидетельство Вход
Вход












 Организация систематической подготовки учащихся к успешному решению геометрических задач в рамках итоговой государственной аттестации в 9 и 11 классах (53.8 KB)
Организация систематической подготовки учащихся к успешному решению геометрических задач в рамках итоговой государственной аттестации в 9 и 11 классах (53.8 KB)
 0
0 1272
1272 47
47 Нравится
0
Нравится
0


