Методическая разработка
Организация дистанционного изучения темы
«Элементы комбинаторики»
Автор: преподаватель ГБПОУ «Педагогического колледжа № 4 Санкт-Петербурга»
Мартусевич Татьяна Олеговна
1 урок
Правила суммы и произведения
Теоретическая часть
В повседневной жизни нередко встречаются задачи, которые имеют несколько различных вариантов решения. Чтобы сделать правильный выбор, важно не пропустить ни один из них. Для этого надо уметь осуществлять перебор всех возможных вариантов или подсчитывать их число.
Запишите тему: Элементы комбинаторики
Запишите определение: Задачи, в которых требуется осуществить перебор всех возможных вариантов решения или подсчитать их число называются комбинаторными.
Область математики, в которой изучают комбинаторные задачи, называется комбинаторикой.
Комбинаторика возникла в XVI в., и первоначально в ней рассматривались комбинаторные задачи, связанные в основном с азартными играми.
В процессе изучения таких задач были выработаны некоторые общие подходы к их решению, получены формулы для подсчета числа различных комбинаций.
Запишите правило суммы:
Если объект a можно выбрать m способами, а объект b − k способами (не такими, как a), то выбор «либо a, либо b» можно осуществить m + k способами.
Прочитайте пример задачи с решением, кратко запишите этот пример в тетрадь (рассуждения записывать не надо).
Задача 1. На тарелке лежат 5 яблок и 4 апельсина. Сколькими способами можно выбрать один плод?
Решение. По условию задачи яблоко можно выбрать пятью способами, апельсин — четырьмя. Так как в задаче речь идет о выборе «либо яблоко, либо апельсин», то его, согласно правилу сложения, можно осуществить 5 + 4 = 9 способами.
Запишите правило умножения:
Если объект a можно выбрать m способами, а объект b − k способами, то пару (a, b) можно выбрать mk способами.
Прочитайте примеры задач с решением, кратко запишите 2,4,5,6 задачи в тетрадь (рассуждения записывать не надо, только краткое условие и решение).
Задача 2. На тарелке лежат 5 яблок и 4 апельсина. Сколькими способами можно выбрать пару плодов, состоящую из яблока и апельсина?
Решение. По условию задачи, яблоко можно выбрать пятью способами, апельсин — четырьмя. Так как в задаче речь идет о выборе пары (яблоко, апельсин), то ее, согласно правилу умножения, можно выбрать 5 ⋅ 4 = 20 способами.
Задача 3. Сколько всего двузначных чисел можно составить из цифр 7, 4 и 5 при условии, что они в записи числа не повторяются?
Решение. Чтобы записать двузначное число, надо выбрать цифру десятков и цифру единиц. Согласно условию, на месте десятков в записи числа может быть любая из цифр 7, 4 и 5. Другим словами, выбрать цифру десятков можно тремя способами. После того как цифра десятков определена, для выбора цифры единиц остается две возможности, поскольку цифры в записи числа не должны повторяться. Так как любое двузначное число — это упорядоченная пара, состоящая из цифры десятков и цифры единиц, то ее выбор, согласно правилу умножения, можно осуществить шестью способами (3 ⋅ 2 = 6).
Правила сложения и умножения, сформулированные для двух объектов, можно обобщить и на случай t объектов.
Задача 4. Сколько трехзначных чисел можно составить, используя цифры 7, 4 и 5?
Решение. В данной задаче рассматриваются трехзначные числа. Так как цифры в записи этих чисел могут повторяться, то цифру сотен, цифру десятков и цифру единиц можно выбрать тремя способами каждую. Поскольку запись трехзначного числа представляет собой упорядоченный набор из трех элементов, то, согласно правилу произведения, его выбор можно осуществить 27 способами, так как 3 ⋅ 3 ⋅ 3 = 27.
Задача 5. Сколько всего четырехзначных чисел можно составить из цифр 0 и 3?
Решение. Запись четырехзначного числа представляет собой упорядоченный набор (кортеж) из четырех цифр. Первую цифру — цифру тысяч — можно выбрать только одним способом, так как запись числа не может начинаться с нуля. Цифрой сотен может быть либо ноль, либо три, т. е. имеется два способа выбора. Столько же способов выбора имеется для цифры десятков и цифры единиц.
Итак, цифру тысяч можно выбрать одним способом, цифру сотен — двумя, цифру десятков — двумя, цифру единиц — двумя. Чтобы узнать, сколько всего четырехзначных чисел можно составить из цифр 0 и 3, согласно правилу умножения, способы выбора каждой цифры надо перемножить: 1 ⋅ 2 ⋅ 2 ⋅ 2 = 8.
Таким образом, имеем 8 четырехзначных чисел.
Задача 6. Сколько трехзначных чисел можно записать с помощью цифр 0, 1, 3, 6, 7 и 9, если каждая из них может быть использована в записи только один раз?
Решение. Так как запись числа не может начинаться с нуля, то цифру сотен можно выбрать пятью способами; выбор цифры десятков можно осуществить также пятью способами, поскольку цифры в записи числа не должны повторяться, а одна из шести данных цифр будет уже использована для записи сотен; после выбора двух цифр (для записи сотен и десятков) выбрать цифру единиц из данных шести можно четырьмя способами. Отсюда, по правилу умножения, получаем, что трехзначных чисел (из данных шести цифр) можно образовать 5 ⋅ 5 ⋅ 4 = 100 способами.
Практическая часть
Используя правило произведения, решите самостоятельно следующие задачи:
Школьники из Волгограда собрались на каникулы поехать в Москву, посетив по дороге Нижний Новгород. Из Волгограда в Нижний Новгород можно отправиться на теплоходе или поезде, а из Нижнего Новгорода в Москву — на самолете, теплоходе или автобусе. Сколькими различными способами ребята могут осуществить свое путешествие? Назовите все возможные варианты этого путешествия.
Сколько различных двузначных чисел можно записать с помощью цифр 3, 4, 5 и 6? Сколько различных двузначных чисел можно записать, используя при записи числа каждую из указанных цифр только один раз? Чтобы ответить на первый вопрос задачи используйте задачу 4. Чтобы ответить на второй вопрос задачи используйте задачу 6, но учтите, что у вас нет нуля.
Девять школьников, сдавая экзамены по математике, русскому и английскому языку, получили отметки «4» и «5». Можно ли утверждать, что по крайней мере двое из них получили по каждому предмету одинаковые отметки? Сколько всевозможных трехзначных чисел можно составить из цифр 1, 2, 3 и 4 так, чтобы цифры в записи числа не повторялись? Изменится ли решение этой задачи, если вместо цифры 4 будет дана цифра 0?
Сколько всевозможных четырехзначных чисел можно составить, используя для записи цифры 1, 2, 3 и 4? Какова разность между самым большим и самым малым из них?
Из цифр 0,1,2,3,4 составляют всевозможные пятизначные числа, причем так, что в записи каждого числа содержатся все данные цифры. Сколько можно составить таких чисел? Чему будет равна разность между наибольшим и наименьшим из полученных чисел?
Проверьте себя:
1.
В
 НН М
НН М
Из Волгограда в Нижний Новгород выбор из 2 видов транспорта (теплоход т и поезд п), а из Нижнего Новгорода в Москву – из 3 (самолет с, теплоход т, автобус а). Получаем 2•3=6. Ответ 6 вариантов. 6 это мало, можно все перебрать:
ТС;ТТ;ТА;ПС;ПТ;ПА.
2.
Двузначное число обозначим двумя точками: • •
Выпишем данные цифры: 3,4,5,6.
Ответим на первый вопрос. На первое место числа можно поставить любую из 4 цифр и на второе место любую из 4 цифр:
4•4=16. Получится 16 чисел.
Ответим на второй вопрос: если нельзя повторять цифры, то когда мы одну возьмем, останется только 3:
4•3=12. Получится 12 чисел. Можно убедиться в этом, выписав их все, используя метод перебора от меньшего к большему, чтобы ничего не пропустить:
33 34 35 36
43 44 45 46
53 54 55 56
63 64 65 66
3. Рассуждайте так: пришел школьник на экзамен по математике, сколько у него возможностей получить отметку (4 или 5, то есть 2 возможности)? Потом на экзамен по русскому, сколько вариантов получить отметку? И на английский… Итак 2•2•2=8. Всего 8 вариантов распределения отметок. Можно выписать их все, чтобы убедиться: 444;445;454;455;544;545;554;555. 8 вариантов распределения оценок. А учеников 9, значит, хотя бы у двоих оценки совпадут.
4. • • • • 1,2,3,4 -4 цифры
1) 4•4•4•4=256
2) 4444-1111=3333
5.
• • • • • 0,1,2,3,4 – 5 цифр, но есть 0!
На первое место в записи числа нельзя ставить 0! Поэтому чтобы поставить цифру на 1 место у нас выбор только из 4 цифр, когда одну возьмем, останется тоже 4, потому что теперь уже можно брать 0, возьмем цифру, поставим на 2 место, останется только 3 цифры, потом 2, потом 1. Потому что в этой задаче в условии сказано, что нельзя повторять цифры в записи числа = «в записи каждого числа содержатся все данные цифры»
Итак:
4•4•3•2•1=96
43210-10234=32976
Самооценка:
5 – сделали четкий структурированный конспект, все поняли, самостоятельно верно решили 4-5 задач.
4 – сделали четкий структурированный конспект, все поняли, самостоятельно верно решили 2-3 задачи.
3 – сделали четкий структурированный конспект, все поняли только после знакомства с верными решениями.
2 – ничего не делали, ничего не поняли.
Физкультминутка:
https://www.youtube.com/watch?v=eg4Ep9lR_tU&app=desktop
2 урок
Размещения и сочетания
Теоретическая часть
Запишите определение:
Размещение с повторениями из k элементов по m элементов — это кортеж длины m, составленный из m элементов k-элементного множества.
Вспомните, где вы встречали слово кортеж: свадебный кортеж, президентский кортеж – элементы следуют друг за другом в строгом порядке. Порядок важен!
Запишите формулу:
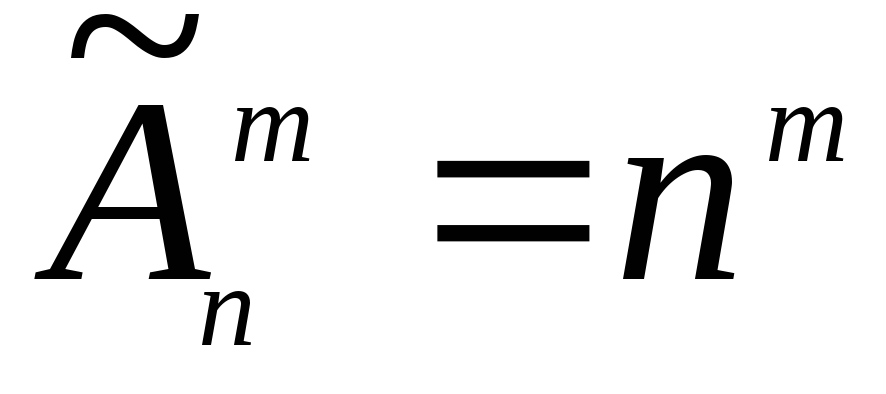
Запишите примеры задач:
Сколько различных двузначных чисел можно записать с помощью цифр 3, 4, 5 и 6?
Эту задачу мы с вами уже решили по правилу произведения. Теперь решим по формуле. Порядок важен для нас, повторяться можно, поэтому это размещение с повторениями. Выбираем из 4 – внизу будет 4, выбираем 2 цифры – наверху будет 2.
Имеется лак двух цветов: красный и черный. Сколько существует вариантов распределения цветов на 10 ногтях?
Нам важно, ноготь, на каком пальце будет красный, а на каком - черный, поэтому порядок важен для нас. Мы можем все выкрасить в 1 цвет или один или 2 любых ногтя покрасить в красный, а остальные в чёрный или 3 или наоборот. Мы можем решить эту задачу по правилу произведения, выбирая для каждого из 10 ногтей из 2 цветов: 2•2•2•2•2•2•2•2•2•2=1024.
А можем выбрать формулу ![]() Внизу 2 – выбираем из 2, наверху – 10 – выбираем из 10:
Внизу 2 – выбираем из 2, наверху – 10 – выбираем из 10:
210=1024.
Запишите определение, формулу и пример задачи:
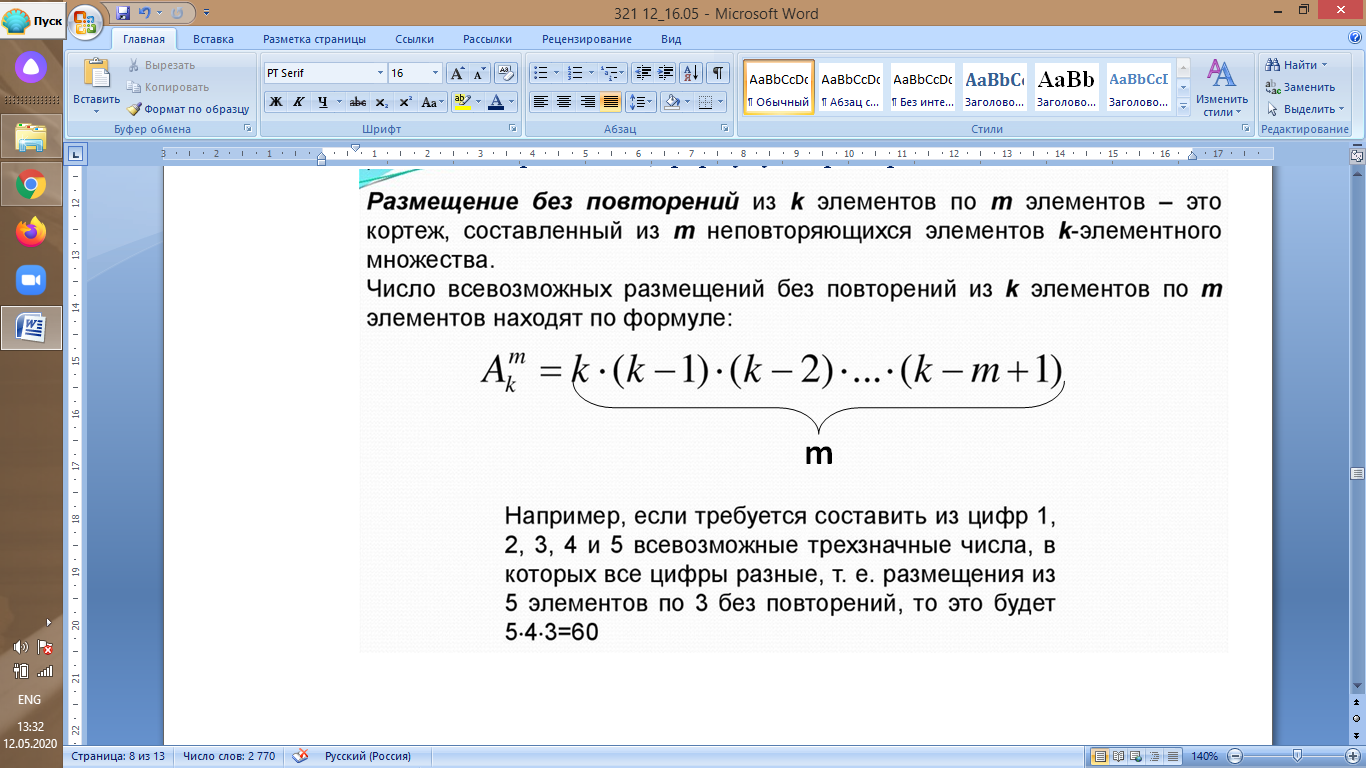
Обратите внимание, что количество множителей m, поэтому можно не считать, сколько будет в 3 скобке, просто каждый следующий множитель на 1 меньше предыдущего, а их количество равно m. В задаче 3 множителя.
Запишите: Задача 2. Сколько всевозможных трехзначных чисел можно записать, используя цифры 7, 4 и 5, так, чтобы цифры в записи числа не повторялись?
Заметим, что в данном случае разные числа получаются в результате перестановки цифр. Поэтому размещения из k элементов по k элементов называют перестановками из k элементов без повторений.
Число перестановок без повторений из k элементов обозначают Pk и подсчитывают по формуле
Pk = k!, где k! = 1 ⋅ 2 ⋅ 3 ⋅ … ⋅ k
и k! читают «k факториал». Считают, что 1! = 1, 0! = 1. Например, 5! = 1 ⋅ 2 ⋅ 3 ⋅ 4 ⋅ 5 = 120; 7! = 1 ⋅ 2 ⋅ 3 ⋅ 4 ⋅ 5 ⋅ 6 ⋅ 7 = 5040.
Запишите определение, формулу и пример задачи:
Сочетание без повторения из k элементов по m элементов — это m-элементное подмножество множества, содержащего k элементов.
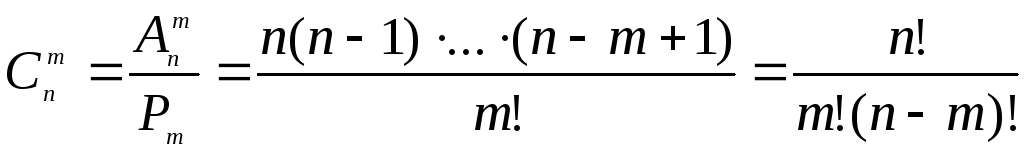
Задача. На прямой взяли десять точек. Сколько всего получилось отрезков, концами которых являются эти точки?
В этой задаче порядок роли не играет (отрезок AВ и отрезок ВA — это один и тот же отрезок). Порядок не важен. Комбинации в этой задаче являются двухэлементными подмножествами, образованными из 10 данных элементов (точек). Такие подмножества в комбинаторике называются сочетаниями без повторений из 10 элементов по 2. Их число можно найти по формуле: .
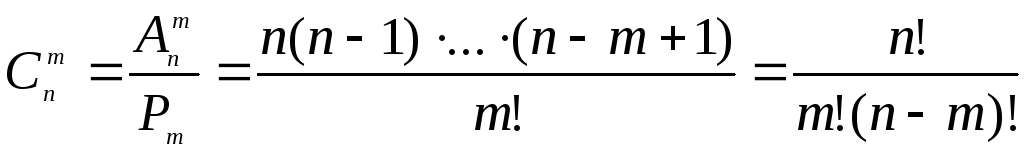
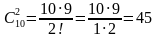
Конечно, применение формул облегчает подсчет числа возможных вариантов решений той или иной комбинаторной задачи. Однако чтобы воспользоваться формулой, необходимо определить вид соединений (комбинаций), о которых идет речь в задаче, что бывает сделать не очень просто. Для этого воспользуемся алгоритмом (запишите алгоритм в тетрадь):
Алгоритм
Порядок важен?
Да – это размещение. Нет – это сочетание.
Если это размещение. Второй вопрос: элементы могут повторяться? Да – размещение с повторениями. Нет – размещение без повторений.
Если элементы просто переставляются местами, то это перестановка.
Практическая часть
Решения задач записывайте на чистой странице тетради, четко, яркими чернилами для последующего фотографирования!
В следующих задачах рассматриваются размещения из k элементов по m; решите, используя формулы размещений и перестановки:
Из 20 учащихся класса надо выбрать старосту, его заместителя и редактора газеты. Сколькими способами это можно сделать?
В классе изучаются 7 предметов. В среду 4 урока, причем все разные. Сколькими способами можно составить расписание на среду?
В соревновании участвуют 10 человек. Сколькими способами могут распределиться между ними места?
Сколько всевозможных трехзначных чисел можно записать, используя цифры 3, 4, 5 и 6?
В следующих задачах рассматриваются сочетания из k элементов по m, решите, используя формулу для сочетаний:
Сколькими способами можно выбрать из 6 человек комиссию, состоящую из трех человек?
Сколькими способами можно выбрать 4 краски из 10 различных красок?
Решите следующие задачи, используя формулы. Выбирайте формулу по алгоритму:
Сколько словарей необходимо переводчику, чтобы он мог переводить текст с любого из четырех языков — русского, английского, немецкого и французского — на любой другой из этих языков?
Государственные флаги некоторых стран состоят из трех горизонтальных полос разного цвета. Сколько различных вариантов флагов с белой, синей и красной полосами можно составить?
Мальчик выбрал в библиотеке 5 книг. По правилам библиотеки одновременно можно взять только 2 книги. Сколько у мальчика вариантов выбора двух книг из пяти?
Аня, Боря, Вера и Гена — лучшие лыжники школы. На соревнования надо выбрать троих из них. Сколькими способами можно это сделать?
При изготовлении авторучки корпус и колпачок могут иметь одинаковый или разный цвет. На фабрике имеется пластмасса четырех цветов: белого, красного, синего и зеленого. Какие отличающиеся по цвету ручки можно изготовить?
На прямой взяли 4 точки. Сколько всего получилось отрезков, концами которых являются эти точки?
В соревнованиях участвуют 5 футбольных команд. Каждая команда играет один раз с каждой из остальных команд. Сколько матчей будет сыграно.
Самооценка по теме «правила суммы и произведения» - …
Сфотографируйте свои решения: условие-формула-вычисления (только решения задач); самооценку в 14 и загрузите этот файл под вашей фамилией в вашу папку 321 16.05 по ссылке:
3 урок
Проверьте себя:






6

 Получите свидетельство
Получите свидетельство Вход
Вход












 Организация дистанционного изучения темы "Элементы комбинаторики" (11.29 MB)
Организация дистанционного изучения темы "Элементы комбинаторики" (11.29 MB)
 0
0 692
692 5
5 Нравится
0
Нравится
0


