Олимпиадные задания по математике

5 класс

1. На карточках записаны числа 415, 43, 7, 8, 74, 3 (см. рис.) . Расположите карточки в ряд так, чтобы получившееся десятизначное число было наименьшим из возможных.

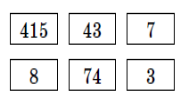
Решение: В наименьшем числе наибольшие разряды должны быть наименьшими из возможных, поэтому первая карточка 3, затем 415, следом 43, 74, 7, 8. Получившееся число – 3415437478.

1. Разрежьте фигуру, изображённую на рисунке, на три части так, чтобы в каждой из частей была снежинка и из этих частей можно было бы сложить квадрат. Нарисуйте, как вы разрезаете фигуру и каким образом складываете квадрат.

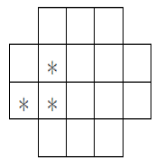
Решение: Всего 16 клеточек, так что квадрат будет 4х4.

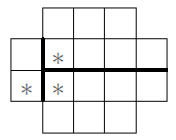
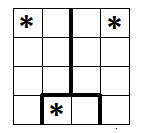Один из вариантов

1. Одну сторону прямоугольника увеличили в 3 раза, а другую уменьшили в 2 раза и получили квадрат. Чему равна сторона квадрата, если площадь прямоугольника 54 м² ?

Решение: Пусть х – одна сторона, прямоугольника, а у – другая. После преобразования прямоугольника получили квадрат со сторонами 3х и у/2, то есть 3х = у/2 или же у = 6х. Тогда х ^. у = 6х ^. х = 54, значит, х = 3, а сторона квадрата равна 9.

1. На доске записано число 61. Каждую минуту число стирают с доски и записывают на это место произведение его цифр, увеличенное на 13. То есть, через одну минуту на доске будет записано 19 (6ˑ1+13=19). Какое число можно будет прочитать на доске через час?

Решение: Проделав несколько раз указанную операцию, заметим, что значения образуют цикл (19, 22, 17, 20, 13, 16), следовательно, через час на доске будет число 16.

1. Перед гномом лежат три кучки бриллиантов: 17; 21 и 27 штук. В одной из кучек лежит один фальшивый бриллиант. Все бриллианты имеют одинаковый вид, все настоящие бриллианты весят одинаково, а фальшивый отличается от них по весу. У гнома есть чашечные весы без гирь. Гному надо за одно взвешивание найти кучку, в которой все бриллианты настоящие. Как это сделать?

Решение: Выберем, например, первую и вторую кучки и уберём из второй кучки 4 бриллианта, после чего взвесим их (17 против 17). Если весы в равновесии, то в первой кучке точно все бриллианты настоящие. Если же одна из них перевешивает, то в третьей кучке точно все бриллианты настоящие.

6 класс

1. Дано трехзначное число ABB, произведение цифр которого  — двузначное число AC, произведение цифр этого числа равно C (здесь, как в математических ребусах, цифры в записи числа заменены буквами; одинаковым буквам соответствуют одинаковые цифры, разным  — разные). Определите исходное число.

Решение: Если произведение цифр числа АС равно С, то, очевидно, А=1. Значит, А ^. В ^. В = В²

Квадрат числа начинается на 1, значит, В = 4.

Ответ: 144.

1. У каждого из тридцати шестиклассников есть одна ручка, один карандаш и одна линейка. После их участия в олимпиаде оказалось, что 26 учеников потеряли ручку, 23 – линейку и 21 – карандаш. Найдите наименьшее возможное количество шестиклассников, потерявших все три предмета.

Решение: Для решения задачи сперва необходимо определить общее количество утерянных предметов. Для этого суммируем количество утерянных ручек, карандашей и линеек. Получим: 26 + 23 + 21 = 70 предметов. Находим общее количество двух любых предметов всех школьников, которые участвовали в олимпиаде. Для этого умножаем их количество на 2. В таком случае получим: 30 ^. 2 = 60 предметов. В таком случае, для того, чтобы определить какое максимальное количество учеников могло потерять все 3 предмета, необходимо от общего числа утерянных предметов отнять 60. Получим: 70 – 60 = 10 человек.

1. В равенстве ТИХО + ТИГР = СПИТ замените одинаковые буквы одинаковыми цифрами, а разные буквы – разными цифрами так, чтобы ТИГР был бы как можно меньше (нулей среди цифр нет).

Решение: Для того, чтобы ТИГР был бы как можно меньше, надо рассматривать самые маленькие цифры для него и подставлять на место цифр в других двух числах. Для начала возьмем Т=1, тогда имеем: 1ИХО+1ИГР=СПИ1. «С» у нас будет либо 2, либо 3, это зависит уже от И. Если С взять как 2, а И как 3, то ТИГР получится меньше = 13ХО+13ГР=2СП1. Тогда П - 6 или 7. Возьмем Г = 4, а Р = 5 (самые маленькие оставшиеся цифры), тогда: 13ХО+1345=2СП1, отсюда уже легко получить, что О=6, Х=8 и П=7.

Ответ:  1386 + 1345 = 2731 

1. На прямой отметили несколько точек. После этого между каждыми двумя соседними точками поставили еще по точке. Аналогичную операцию проделали еще три раза. В результате, на прямой оказалось ровно 65 точек. Сколько точек было на прямой первоначально?

Решение: Если есть некоторое количество точек, то количество отрезков, на которые они разбивают прямую, исключая внешние, на один меньше количества точек. То есть если вначале было х точек, То в первый раз добавилось (х – 1) точка, во второй – (2х – 2) точки, в третий – (4х –4) точки, в четвёртый – (8х – 8) точек. Всего их стало (16х – 15) точек или 65. Решая это уравнение, получаем, что первоначально на прямой было 5 точек.

Ответ: 5 точек.

1. Путь из Белорецка в Уфу Арсен на «семерке» проезжает за 6 часов, а Михаил на «Мицубиси» - за 12 часов. Они выехали из Уфы и Белорецка одновременно. Через какое время они встретятся?

Решение: Арсен за час проезжает 1/6 часть пути, а Михаил – 1/12. Таким образом, скорость сближения – 1/6 + 1/12 = 3/12 = ¼. Следовательно, они встретятся через 4 часа.

Ответ: 4 часа

1. класс

1. Жулик попросил у продавца Аникбека бутылку лимонада за 45 рублей, дав фальшивую 500-рублевую купюру. Сдачи у Аникбека не было, и он разменял купюру в соседнем ларьке у продавца Юлая. Когда жулик ушел, Юлай понял, что купюра фальшивая, и Аникбеку пришлось отдать ему настоящие 500 рублей. Какой убыток понес Аникбек?

Решение: Аникбек отдал жулику бутылку лимонада (45 руб), сдачу (455 руб) и 500 рублей Юлаю вместо фальшивой купюры. Итого – 45 + 455 + 500 = 1000.

Ответ: 1000 рублей.

1. В пяти пакетах лежат конфеты. В первом 7, во втором 8, в третьем 9, в четвёртом 11 и в пятом 14. Из любого пакета в любой другой можно переложить любое возможное число конфет. Можно ли за два перекладывания добиться равного числа конфет во всех пакетах?

Решение: Общее число конфет равно 7 + 8 + 9 + 11 + 14 = 49 – не делится на 5, поэтому требуемое перекладывание невозможно.

Ответ: нет.

1. Можно ли вместо звёздочек поставить четыре последовательных натуральных чисел, чтобы равенство ** - **=5 стало верным?

Решение: Обозначим последовательные числа, например, п – 1, п, п + 1, п + 2. Тогда возможны следующие варианты (из полного перебора убираем те, которые заведомо не могут дать 5 – когда из меньшего числа вычитается большее):

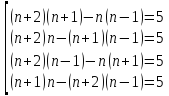
Решая эту совокупность, получаем решение 1; 2; 3; 4 (4 ^. 2 – 3 ^. 1 = 5)

1. Докажите, что число 7^{1 000 000 009} + 9^{1 000 000 007} делится на 8.

Решение: 7 = (8 – 1), 9 = (8 + 1). По формулам сокращённого умножения (8 + 1)ⁿ = 8m + 1 для любого п; (8 – 1)^2k+1 = 8l -1. Складывая, получим (8l – 1) + (8т + 1) = 8(l + m), следовательно, указанная сумма делится на 8.

1. Существует ли натуральное число n такое, числа 11n+5 и 19n+2 делятся на 2?

Решение: Заданные числа разной чётности (участники должны это доказать), поэтому ответ отрицательный.

Ответ: нет.

8 класс

1. По кругу расставлены 9 нулей и единиц, причём не все расставленные числа равны. За один ход между каждыми двумя соседними числами 0, если эти числа равны, и 1, если они не равны. После этого старые числа стираются. Могут ли через некоторое время все числа стать равными?

Решение: Ясно, что комбинация из девяти единиц раньше, чем девять нулей, получиться не может. Если же получилось девять нулей, то на предыдущем ходу нули и единицы должны были чередоваться, что невозможно, так как их всего нечетное количество.

Ответ: нет.

2. Электронные часы показывают время в стандартном формате (например, 20:27). Найдите наибольшее возможное произведение цифр на таких часах.

Решение: Понятно, что не будем рассматривать время, в которых присутствует 0. Если первая цифра 2, то вторая не может быть больше 3, то есть их произведение равно 6, в то время как с первой цифрой 1 мы можем получить произведение 9, что больше, чем 6. Следовательно, первые две цифры 1 и 9. Во вторых цифрах произведение будет максимальным, когда сами цифры максимальны, т. е. 5 и 9. Таким образом, наибольшее произведение равно 405. Правильный ответ без обоснований следует оценивать 0 баллов.

Ответ: 405.

3. У шахматной доски вырезали две противоположные угловые клетки. Можно ли оставшуюся часть разрезать на прямоугольники 1^х2?

Решение: Каждый из прямоугольников закрывает 2 клетки – одну белую и одну чёрную, следовательно, количество белых и чёрных клеток должно быть одинаково. Противоположные угловые клетки одного цвета, поэтому, вырезав их, мы нарушаем это равенство (30 клеток одного и 32 клетки другого цветов). Поэтому ответ на вопрос задачи отрицательный. Правильный ответ без обоснований – 0 баллов.

Ответ: нет.

4. Найдите наименьшее натуральное число, делящееся на 36, в записи которого участвуют все 10 цифр по 1 разу.

Решение: Если число должно быть наименьшим, то меньшие цифры в старшие разряды числа. Если число делится на 36, то оно делится на 9, и на 4. Если число делится на 9, то и сумма его цифр делится на 9. Так как используются все цифры, то их сумма равна 45 и это условие выполняется. Чтобы число делилось на 4, нужно, чтобы число, образованное последними двумя цифрами, делилось на 4 и при этом было наибольшим. Такое число 96. С учётом всего сказанного записываем ответ. Указание числа без обоснования – 1 балл.

Ответ: 1023457896

5. Давным-давно в стране СССР имелись в обращении 3-копеечные и 5-копечные монеты. Докажите, что можно было набрать любу сумму, большую 7 копеек, только такими монетами.

Решение: при делении на 3 у нас есть 3 остатка: 0, 1 и 2. Если сумма делится на 3, то её можно выдать одними трёх копеечными монетами. Если она равна 3k + 1 = 3(k – 3) + 9 + 1 = 3(k – 3) + 5 +5. Если сумма равна 3k + 2 = 3(k – 1) + 3 + 2 = 3(k – 1) + 5. Аналогичное решение можно основать и на 5-копеечных монетах.

9 класс

1. Петя и Витя ехали вниз по эскалатору. Посередине эскалатора хулиган Витя сорвал с Пети шапку и бросил её на встречный эскалатор. Пострадавший Петя побежал обратно вверх по эскалатору, чтобы затем спуститься вниз и вернуть шапку. Хитрый Витя побежал по эскалатору вниз, чтобы затем подняться вверх и успеть раньше Пети. Кто успеет раньше, если скорости ребят относительно эскалатора постоянны и не зависят от направления движения?

Решение: Два встречных эскалатора фактически образуют движущееся с постоянной скоростью кольцо (на котором можно кататься, как на карусели), относительно которого шапка неподвижна. Встанем около шапки и понаблюдаем за бегом ребят. При этом можно считать, что эскалаторы стоят, а ребята бегут к ним из диаметрально противоположных точек кольца с равными скоростями, но каждый со своей стороны. Теперь очевидно, что они прибегут к шапке одновременно. Однако эти рассуждении верны только при одном условии: Петя должен добежать до верха эскалатора прежде, чем туда приедет шапка (она сама не может пересесть на Петин эскалатор и поехать ему навстречу. Рассмотрен только один случай – 4 балла.

Ответ: Если скорости ребят как минимум вдвое больше скорости эскалатора, то они добегут до шапки одновременно. Иначе первым добежит Витя.

2. У Пети в бутылке было «Фанты» на 10% больше, чем у Вити. Петя отпил из своей бутылки 11% его содержимого, а Витя из своей – 2% содержимого. У кого после этого осталось «Фанты» больше?

Решение: Пусть у Вити в бутылке было а мл «Фанты», тогда у Пети было 1,1а мл. После того, как каждый мальчик отпил из своей бутылки, у Вити осталось 0,98а мл, а у Пети – 0,89 ^. 1,1а = 0,979а мл.

Ответ: у Вити.

3. Как-то раз Алевтина Изольдовна ехала в поезде и, чтобы не скучать, стала заменять буквы названия городов их порядковыми номерами. Когда Алевтина Изольдовна зашифровала пункты прибытия и отправления, то с удивлением обнаружила, что они записываются с помощью всего лишь 2 цифр: 21221 – 211221. Откуда и куда шёл поезд?

Решение. Так как использовались только 1 и 2 то могли использоваться только буквы А(1), Б(2), Й(11), К(12), У(21), Ф(22). Построив, например, дерево вариантов, получим поезд Уфа – Баку.

Ответ: из Уфы в Баку.

4. Решите уравнение в целых числах ху + х – 3у = 4.

Решение:

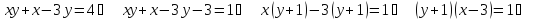
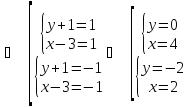
Ответ: {(0; 4), (2; -2)}

5. Высота ромба, проведённая из вершины тупого угла, делит его сторону на отрезки длиной т и п, считая от вершины острого угла. Определите диагонали ромба.

Решение:

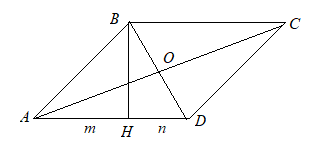
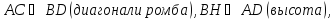
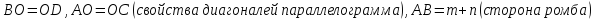
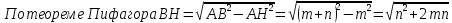
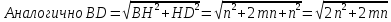
По свойству диагоналей ромба

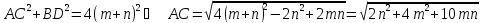
10 класс

1. Сложили числа 9; 99; 999; … ; 99…99 (2018 девяток). Сколько единиц в записи получившейся суммы?

Решение:

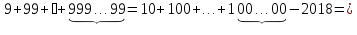
2018 раз 2018 раз

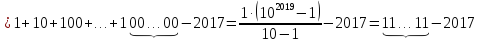
2018 раз 2019 раз

Дальше, выполняя вычитание «столбиком», получаем ответ.

Ответ: 2014 раз.

2. Ольга Алексеевна выписывает последовательно на доску по возрастанию все числа, в которых число нечётных цифр равно числу чётных цифр. Какое число Ольга Алексеевна напишет 50-м?

Решение: т. к. количество чётных и нечётных цифр одинаково, то рассматриваем числа с чётным количеством цифр (2-значные, 4-значные). Легко достигается результат, т. к. в каждом десятке мы берём 5 чисел.

Ответ: 1009.

3. Каждая сторона правильного треугольника разделена на 3 равные части, и соответственные точки деления, считая в одном направлении, соединены между собой. В полученный правильный треугольник вписана окружность радиусом 6 см. Определите стороны исходного треугольника.

Решение: радиус вписанной в правильный треугольник окружности вычисляется по формуле 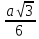, где а – сторона этого треугольника. Найдём сторону из теоремы косинусов: 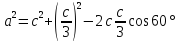. Выполнив все преобразования, получим сторону исходного треугольника 36.

4.Решите уравнение в целых числах 10х + у = х² + у² – 13.

Решение: Преобразуем уравнение

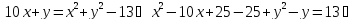
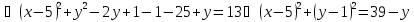
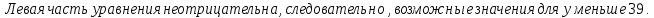
Учитывая, что (у – 1)² 39 – 4, получаем решение

Ответ: (1; 4).

1. Найдите какую-нибудь пару натуральных чисел a и b, больших 1, удовлетворяющих уравнению a¹³ · b³¹ = 6²⁰¹⁵.

Решение:

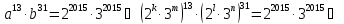
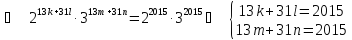
Решая эту систему, получаем k = n = 0; 31; 62; 124, l = m = 13; 26; 39; 52;65. |Отсюда определяются a, b.

11 класс

1. Найдите какую-нибудь пару натуральных чисел a и b, больших 1, удовлетворяющих уравнению a¹³ · b³¹ = 6²⁰¹⁵.

Решение:

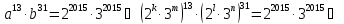
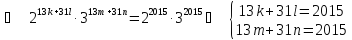
Решая эту систему, получаем k = n = 0; 31; 62; 124, l = m = 13; 26; 39; 52;65. |Отсюда определяются a, b.

2. Плоский угол при вершине правильной треугольной пирамиды равен 90º. Найдите отношение площади боковой поверхности пирамиды к площади её основания.

Решение: т. к. пирамида правильная, то в основании равносторонний треугольник, а боковые стороны – равнобедренные прямоугольные треугольники. Тогда S_бок = 3 ^. 1/2 ^. 2а² = 3а². S_осн =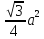

Тогда

3. Решите уравнение

Решение:

4. Если двузначное число разделить на сумму своих цифр, то в частном получится число 3, а в остатке – 7. Найдите такое число.

Решение: Из условия следует, что Т. к. левая часть делится на 7, то и правая должна делиться на 7. Значит, b = 7. Тогда а = 3 и исходное число – 10.

5. Про действительные числа a, b, c известно, что c(a + b + c) b² – 4ac 0.

Решение: Введём вспомогательный квадратный трёхчлен