
Обратные тригонометрические функции и их свойства

Содержание
- Функция y = arcsin x и ее свойства
- Функция y = arccos x и ее свойства
- Функция y = arctg x и ее свойства
- Функция y = arcctg x и ее свойства
y=x
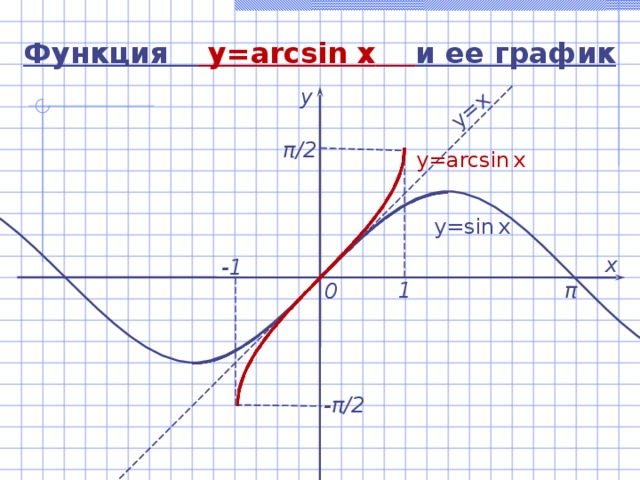
Функция y=arcsin x и ее график
у
π / 2
y=arcsin x
y=sin x
х
-1
1
π
0
- π / 2
![Функция y=arcsin x и ее свойства D(y) = [- 1 ; 1 ] . E(y) = [- π /2 ; π /2 ] . arcsin (-x) = - arcsin x – функция нечетная. Функция возрастает на [- 1 ; 1 ] . Функция непрерывна.](https://fsd.videouroki.net/html/2017/12/17/v_5a36621abad4b/img3.jpg)
Функция y=arcsin x и ее свойства
- D(y) = [- 1 ; 1 ] .
- E(y) = [- π /2 ; π /2 ] .
- arcsin (-x) = - arcsin x – функция нечетная.
- Функция возрастает на [- 1 ; 1 ] .
- Функция непрерывна.
![Функция y=arcsin x Определение Если |а| ≤ 1 , то arcsin а – это такое число из отрезка [- π /2 ; π /2 ] , синус которого равен а . Если |а| ≤ 1 , то arcsin а = t sin (arcsin a) = a sin t = а , - π /2 ≤ t ≤ π /2 ;](https://fsd.videouroki.net/html/2017/12/17/v_5a36621abad4b/img4.jpg)
Функция y=arcsin x
Определение
Если |а| ≤ 1 , то arcsin а – это такое число из отрезка [- π /2 ; π /2 ] , синус которого равен а .
Если |а| ≤ 1 , то
arcsin а = t
sin (arcsin a) = a
sin t = а ,
- π /2 ≤ t ≤ π /2 ;
y=x
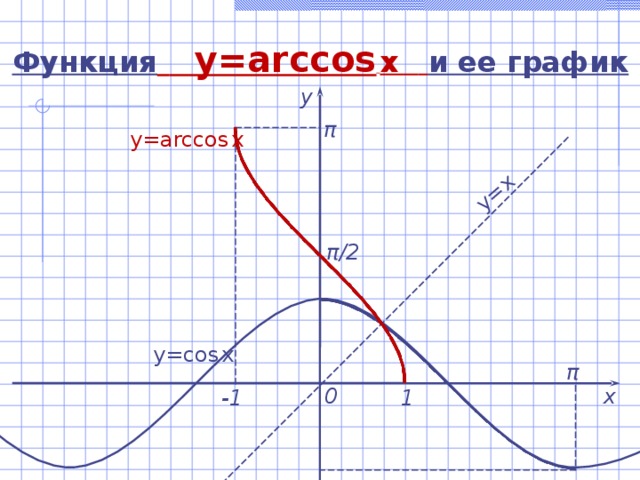
Функция y=arccos x и ее график
у
π
y=arccos x
π /2
y= со s x
π
0
х
-1
1
![Функция y=arccos x и ее свойства D(y) = [- 1 ; 1 ] . E(y) = [ 0 ; π ] . Функция не является ни четной, ни нечетной, arccos (-a) = π – arccos a Функция убывает на [- 1 ; 1 ] . Функция непрерывна.](https://fsd.videouroki.net/html/2017/12/17/v_5a36621abad4b/img6.jpg)
Функция y=arccos x и ее свойства
- D(y) = [- 1 ; 1 ] .
- E(y) = [ 0 ; π ] .
- Функция не является ни четной, ни нечетной, arccos (-a) = π – arccos a
- Функция убывает на [- 1 ; 1 ] .
- Функция непрерывна.
![Функция y=arccos x Определение Если |а| ≤ 1 , то arccos а – это такое число из отрезка [ 0 ; π ] , косинус которого равен а . Если |а| ≤ 1 , то arccos а = t cos (arccos a) = a cos t = а , 0 ≤ t ≤ π ;](https://fsd.videouroki.net/html/2017/12/17/v_5a36621abad4b/img7.jpg)
Функция y=arccos x
Определение
Если |а| ≤ 1 , то arccos а – это такое число из отрезка [ 0 ; π ] , косинус которого равен а .
Если |а| ≤ 1 , то
arccos а = t
cos (arccos a) = a
cos t = а ,
0 ≤ t ≤ π ;
y=x
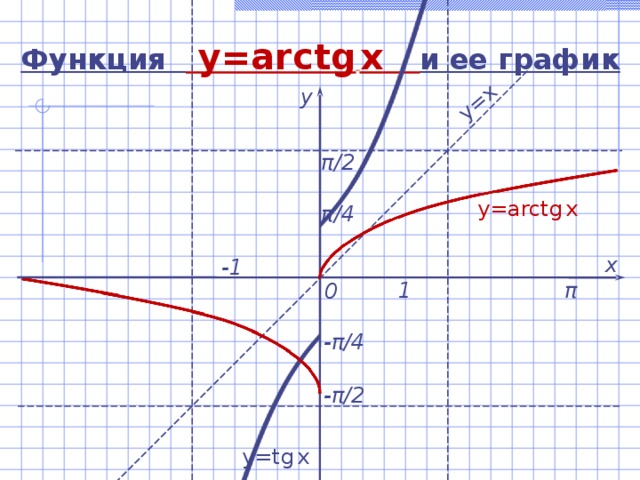
Функция y=arctg x и ее график
у
π / 2
y=arctg x
π /4
х
-1
1
π
0
- π /4
- π / 2
y=tg x

Функция y=arctg x и ее свойства
- D(y) = (- ; + ) .
- E(y) = (- π /2 ; π /2 ) .
- arctg (-x) = - arctg x – функция нечетная.
- Функция возрастает на (- ; + ) .
- Функция непрерывна.

Функция y=arctg x
Определение
arctg а – это такое число из интервала
( - π /2 ; π /2 ) , тангенс которого равен а .
arctg а = t
tg (arctg a) = a
tg t = а ,
- π /2 π /2 ;
y=x
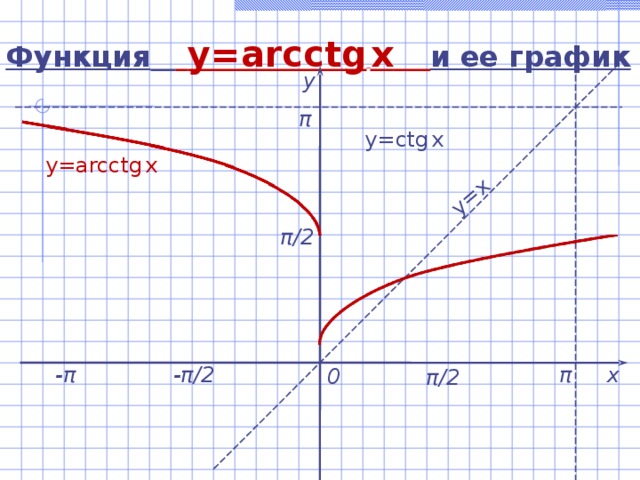
Функция y=arcctg x и ее график
у
π
y= с tg x
y=arc с tg x
π / 2
- π / 2
π
х
- π
0
π / 2

Функция y=arcctg x и ее свойства
- D(y) = (- ; + ) .
- E(y) = ( 0 ; π ) .
3. Функция не является ни четной, ни нечетной, arcctg (-a) = π – arcctg a
4. Функция убывает на (- ; + ) .
5. Функция непрерывна.

Функция y=arcctgx
Определение
ar с ctg а – это такое число из интервала
( 0 ; π ) , котангенс которого равен а .
arc с tg а = t
с tg (arc с tg a) = a
с tg t = а ,
0 π ;

 Получите свидетельство
Получите свидетельство Вход
Вход












 Обратные тригонометрические функции. (528 KB)
Обратные тригонометрические функции. (528 KB)
 0
0 845
845 45
45 Нравится
0
Нравится
0


