Министерство здравоохранения Оренбургской области
ГАПОУ «Оренбургский областной медицинский колледж»
Методическая разработка
по дисциплине БД.04 МАТЕМАТИКА
«Объемы тел»
| Автор: | Данилова Екатерина Валерьевна, преподаватель математики высшей квалификационной категории |
.
Оренбург 2023
Аннотация
Методическая разработка предназначена для оказания помощи в преподавании и изучении темы «Объемы тел» на первом курсе на базе основного общего образования. В пособии содержится теоретический материал, представлены примеры решения задач с привязкой к медицине и смежным наукам, опорный конспект для обучающегося. Задания составлены таким образом, чтобы можно было осуществить проверку теоретических знаний и практических умений.
Содержание
| Технологическая карта занятия ………………………….…………………………………. | 4 |
| Ход занятия …………………………………..……………………........................................ | 8 |
| Список источников …………………………………….……………………………………. | 17 |
| Приложение ………………………………………………………………………………….. | 18 |
Технологическая карта занятия
Тема: «Объемы тел».
Цель: Ввести понятие объема тел, его свойств, единиц измерения объема, познакомить с формулами нахождения объема прямоугольного параллелепипеда, куба, прямой и наклонной призм, пирамиды, цилиндра, конуса и шара.
Задачи:
Образовательные:
-
выявить уровень усвоения понятий: многогранник, куб, параллелепипед, прямая и наклонная призма, пирамида, цилиндр, конус, шар и их элементов;
-
формировать понятия: объем, свойства объема, единицы измерения объема, объем прямоугольного параллелепипеда, куба, прямой и наклонной призм, пирамиды, цилиндра, конуса и шара;
-
формировать умение находить объемы многогранников и тел вращения.
Развивающие:
-
формирование умения работать самостоятельно и в команде;
-
продолжать работу по формированию и совершенствованию приемов умственной деятельности: анализ, сравнение, обобщение, аналогия, алгоритмизация, критического мышления.
Воспитательные:
-
формировать представления об идеях и методах математики как форме описания и методе познания действительности;
-
воспитывать культуру общения, навыки самоконтроля и взаимоконтроля; формировать познавательные интересы и мотивы самосовершенствования.
Планируемые образовательные результаты:
Личностные:
-
развитие способности оценивать ситуацию и принимать осознанные решения;
-
воспитание аккуратности, точности, самостоятельности, привитие навыков групповой работы, сотрудничества, готовности и способности к образованию и самообразованию.
Метапредметные:
-
воспитание у обучающихся ценностного отношения к труду и полученным знаниям;
-
развитие способности и готовности к самостоятельному поиску методов решения практических задач;
-
овладение видами деятельности по получению нового знания, его интерпретации, преобразованию и применению в различных учебных ситуациях;
-
формирование научного типа мышления, владение научной терминологией, ключевыми понятиями и методами;
-
выявлять причинно-следственные связи и актуализировать задачу, выдвигать гипотезу ее решения, находить аргументы для доказательства своих утверждений.
Предметные:
-
ПР 1. владение методами доказательств, алгоритмами решения задач; умение формулировать определения, аксиомы и теоремы, применять их, проводить доказательные рассуждения в ходе решения зада;
-
ПР 9.1. умение оперировать понятиями: точка, прямая, плоскость, пространство, умение использовать при решении задач изученные факты и теоремы планиметрии, оценивать размеры объектов окружающего мира;
-
ПР 9.2. умение оперировать понятиями: расстояние от точки до плоскости, расстояние между прямыми, расстояние между плоскостями, угол между прямой и плоскостью, двугранный угол, угол между плоскостями, перпендикулярность прямых и плоскостей;
-
ПР 9.3. умение оперировать понятиями: скрещивающиеся прямые, угол между прямыми, параллельность прямых и плоскостей;
-
ПР10.1. умение оперировать понятиями: многогранник, сечение многогранника, призма, пирамида, площадь поверхности пирамиды, призмы, умение распознавать правильные многогранники;
-
ПР 10.2. умение оперировать понятиями: куб, параллелепипед;
-
ПР 10.3. умение оперировать понятием фигура;
-
ПР 10.4. умение оперировать понятием поверхность вращения, цилиндр, конус, шар, сфера, сечения фигуры вращения, плоскость, касающаяся сферы, цилиндра, конуса, площадь поверхности конуса, цилиндра, площадь сферы, умение изображать поверхности вращения, их сечения от руки, с помощью чертежных инструментов и электронных средств;
-
ПР 10.5. умение оперировать понятиями: объем куба, прямоугольного параллелепипеда, пирамиды, призмы, цилиндра, конуса, шара;
-
ПР 10.6. умение изображать многогранники, их сечения от руки, с помощью чертежных инструментов и электронных средств;
-
ПР 12. умение вычислять геометрические величины (длина, угол, площадь, объем, площадь поверхности), используя изученные формулы и методы;
-
ПР 14. умение выбирать подходящий изученный метод для решения задачи, распознавать математические факты и математические модели в природных и общественных явлениях, в искусстве; умение приводить примеры математических открытий российской и мировой математической науки.
Формируемые общие компетенции:
-
ОК 3. Принимать решения в стандартных и нестандартных ситуациях и нести за них ответственность.
-
ОК 6. Работать в коллективе и команде, эффективно общаться с коллегами, руководством, потребителями.
-
ОК 7. Брать на себя ответственность за работу членов команды (подчиненных), за результат выполнения заданий.
Основные технологии:
-
технология оценивания образовательных достижений учащихся;
-
технологии личностно-ориентированного развивающего образования;
-
здоровьесберегающая технология;
-
игровая технология обучения;
-
технология обучения в сотрудничестве;
-
технология с использованием ИКТ.
Тип занятия: комбинированное (повторение, изучение нового).
Вид занятия: теоретическое.
Формы организации учебной деятельности: групповая, индивидуальная.
Методы обучения: словесные, наглядные, практические, решение задач, алгоритмизированные.
Формы контроля: устный фронтальный опрос, индивидуальный опрос у доски, решение задач, практическая работа.
Межпредметные связи: физика, химия, обществознание, сестринское дело, лабораторная диагностика, акушерство.
Внутрипредметные связи: многогранники, тела вращения, интеграл.
Оборудование: доска классная, мел, линейка, ПК, телевизор.
Оснащение:
Методическое оснащения занятия:
Рабочая программа учебной дисциплины БД.04 Математика, технологическая карта занятия, методическое пособие для преподавателя.
Дидактическое оснащение занятия: мультимедийная презентация, опорный конспект для обучающегося (Приложение 1), учебник, раздаточный материал (модели многогранников и тел вращения, медицинские предметы: пробирки, колбы, шприцы, клизмы и т.п.).
Литература:
-
Атанасян Л.С, Бутузов В.Ф., Кадомцев С.Б. и др. Математика: алгебра и начала математического анализа, геометрия. Геометрия (базовый и углубленный уровень). Просвещение, 2018г.
План:
-
Организационный момент (1-2 мин).
-
Постановка темы, целей и задач, мотивация (12-15 мин).
Интерактивная игра «Черный ящик».
-
Проверка домашнего задания и актуализация знаний (12-15 мин).
-
Изучение нового (30-35 мин).
-
Понятие объема, его свойства и единицы измерения.
-
- Историческая справка (сообщение «История изучения объемов и единицы измерения»).
- Определение, единицы измерения, свойства объема.
-
Формулы нахождения объема куба, прямоугольного параллелепипеда.
-
Пример решения задачи.
-
Формулы нахождения объема прямой призмы и цилиндра.
-
Примеры решения задач.
-
Формулы нахождения объема наклонной призмы, пирамиды, конуса.
-
Пример решения задачи.
-
Формула нахождения объема шара.
-
Примеры решения задач.
-
Первичное закрепление (15-20 мин).
Практическая работа в парах (измерение элементов тела и вычисление его объема).
-
Домашнее задание (1-2 мин).
-
Рефлексия и подведение итогов (3-5 мин).
Ход занятия
-
Организационный момент (1-2 мин).
Проверка присутствующих и их готовности к занятию.
-
Постановка темы, целей и задач, мотивация (12-15 мин).
-
Объявление темы.
-
Обоснование важности изучения темы и умения определять объем при решении практических задач.
-
Интерактивная игра «Черный ящик».
Правила:
На отдельном столе стоят несколько черных ящиков, в которых спрятаны предметы, имеющее отношение к медицине и связаны с понятием объема. Обучающимся (по желанию) предлагается подойти к столу, выбрать ящик, опустить руку в отверстие сбоку, угадать спрятанный предмет, не доставая его, и объяснить своим одногруппникам что за предмет загадан, обозначив профессию, к которой он имеет отношение, как именно используется, и как связан с понятием объема, не называя самого предмета.
За каждое доступное объяснение и каждый правильный ответ обучающиеся получают по одному жетону.
Примерный перечень предметов: шприц, пробирка, колба, клизма, бутылочка для кормления и т.д.
-
Вовлечение обучающихся в постановку цели занятия.
Обучающимся предлагается вспомнить какие измерения они уже умеют находить у многогранников и тел вращения, и ответить на вопрос что предстоит научиться находить.
-
Проверка домашнего задания и актуализация знаний (12-15 мин).
Задаваемое домашнее задание: Повторить теоретический материал по темам «Многогранники» и «Тела вращения».
Каждому ряду раздается один и тот же набор разверток многогранников и тел вращения: правильная четырехугольная пирамида, прямая треугольная призма, куб, прямоугольный параллелепипед, цилиндр, конус.
Каждому обучающемуся ряда предлагается угадать по развертке загаданное геометрического тело, схематически изобразить его, записать название, записать формулы площади основания, площадей боковой и полной поверхностей.
Первый выполнивший задание выходит к доске, выбирает из предложенных на отдельном столе моделей геометрических тел ту, которая была загадана. На каждое загаданное тело может выйти к доске для ответа только один обучающийся. При проверке обучающийся должен показать модель тела, назвать его, записать формулы.
При проверке оценивается правильность и полнота выполненного задания. После ответа обучающегося на экран выводится эталон ответа. Если задание выполнено полностью и без ошибок, то обучающийся получает 2 жетона, если ответ не полный или есть ошибки, то 1 жетон, при неверном ответе – 0 жетонов.
-
Изучение нового (30-35 мин).
-
Понятие объема, его свойства и единицы измерения.
-
- Историческая справка.
Один из обучающихся выступает с сообщением «История изучения объемов и единицы измерения».
- Определение, единицы измерения, свойства объема.
Преподаватель акцентирует внимание на понятии объема и обучающиеся записывают определение, проводя аналогию с понятием площади. Записываются единицы измерения и свойства площадей и объемов. Все оформляется в виде таблицы в опорном конспекте.
| Площадь | Объем |
| Определение: Площадь многоугольника – это положительная величина той части плоскости, которую занимает многоугольник. | Определение: Объем тела – это положительная величина той части пространства, которую занимает геометрическое тело.
|
| Единицы измерения: 1 км2, 1 м2, 1 дм2, 1 см2, 1 мм2 и т.д. За единицу измерения площадей берут квадрат, сторона которого равна единице измерения отрезков.
| Единицы измерения: 1 м3, 1 дм3, 1 см3 , 1 мм3 и т.д. За единицу измерения объемов принимают куб, ребро которого равно единице измерения отрезков. Куб с ребром 1 см называют кубическим сантиметром и обозначают 1 см3. |
| Свойства:
| Свойства:
|
| Равновеликими называются геометрические фигуры, имеющие равные площади. | Равновеликими называются тела, объемы которых равны. |
-
Формулы нахождения объема куба, прямоугольного параллелепипеда.
Вводятся формулы для вычисления объема куба и прямоугольного параллелепипеда. В таблице опорного конспекта записываются формулы площадей и объемов куба и прямоугольного параллелепипеда.
| Площадь основания | Объем |
| Куб: S=a2 | Куб: V=a3 |
| Прямоугольный параллелепипед: S=ab | Прямоугольный параллелепипед: V=abc |
-
Пример решения задачи.
Обучающимся предлагается решить задачу на вычисление объема прямоугольного параллелепипеда.
Обучающийся давший первым правильный ответ записывает решение на доске.
За правильный ответ обучающийся получает 2 жетона, при наличии ошибки – 1 жетон, при неверном ответе – 0 жетонов.
Задача 1:
Лоток полимерный прямоугольный с крышкой имеет форму прямоугольного параллелепипеда размеры 200 мм, 155 мм, 40 мм. Найдите объем лотка. (Ответ дать в литрах, считая что 1л=1000 мл = 1000000 мм3).
Решение:
Объем лотка можно найти по формуле: V= abc, где a, b, c – длины трех измерений лотка.
V=201540=1240000 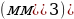 .
.
1240000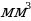 =1,24 л.
=1,24 л.
Ответ: 1,24 л.
-
Формулы нахождения объема прямой призмы и цилиндра.
Вводятся формулы для вычисления объема прямой призмы и цилиндра. В таблице опорного конспекта записываются формулы площадей и объемов призмы и цилиндра.
| Площадь основания | Объем |
| Прямая призма: Формула площади основания прямой призмы зависит от того какая фигура в основании. Например: S= S= S= Sпарал= Sпарал= Sпарал= | Прямая призма: V=SоснH |
| Цилиндр: S=R2 | Цилиндр: V=R2H (L=H) |
-
Примеры решения задач.
Обучающимся предлагается решить на выбор задачу на вычисление объема прямой призмы или цилиндра.
Обучающийся давший первым правильный ответ записывает решение на доске.
За правильный ответ обучающийся получает 2 жетона, при наличии ошибки – 1 жетон, при неверном ответе – 0 жетонов.
Задача 2:
Тело поджелудочной железы имеет форму приближенную к трёхгранной (треугольной) призме. Предположим, что его длина у человека весом 60 кг составляет 18 мм, а разрез, являющийся основанием призмы, представляет собой треугольник с высотой 7 мм и основанием 8 мм. Найдите примерный объем тела поджелудочной железы.
Решение:
Площадь основания призмы можно найти по формуле: S= 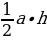 .
.
Тогда объем можно найти по формуле: 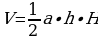 .
.
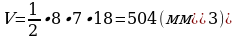 .
.
Ответ: 504 мм3.
Задача 3:
Пробирка для забора крови имеет форму цилиндра с диаметром 16 мм и высотой 100 мм. Какой примерный объем крови сдал пациент, если в пробирку было набрано крови ровно половину возможного объема? (Принять  Ответ дать в мл и округлить до целого числа считая что 1 мл = 1000 мм3).
Ответ дать в мл и округлить до целого числа считая что 1 мл = 1000 мм3).
Решение:
Объем пробирки можно найти по формуле: V=R2H.
Радиус пробирки R=D:2. R=16:2=8 (мм).
Тогда объем забранной крови можно найти по формуле:  .
.
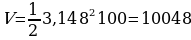 (мм3).
(мм3).
10048 мм3  10 мл.
10 мл.
Ответ: 10 мл.
Задача 4:
Контейнер для биологического материала цилиндрической формы имеет размеры внутренний диаметр 38 мм, а высота до резьбы 53 мм. Найдите примерный объем контейнера. (Принять  Ответ дать в мл и округлить до целого числа считая что 1 мл = 1000 мм3).
Ответ дать в мл и округлить до целого числа считая что 1 мл = 1000 мм3).
Решение:
Объем контейнера можно найти по формуле: V=R2H.
Радиус контейнера R=D:2. R=38:2=19 (мм).
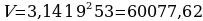 (мм3).
(мм3).
60077,62 мм3  60 мл.
60 мл.
Ответ: 60 мл.
-
Формулы нахождения объема наклонной призмы, пирамиды, конуса.
Вводятся формулы для вычисления объема наклонной призмы, пирамиды и конуса. В таблице опорного конспекта записываются формулы площадей и объемов наклонной призмы, пирамиды и конуса.
| Площадь основания | Объем |
| Наклонная призма: Формула площади основания наклонной призмы зависит от того какая фигура в основании. | Наклонная призма: V=SоснH |
| Пирамида: Формула площади основания пирамиды зависит от того какая фигура в основании. | Пирамида: |
| Конус: S=R2 | Конус: |
-
Пример решения задачи.
Обучающимся предлагается решить задачу на вычисление объема конуса.
Обучающийся давший первым правильный ответ записывает решение на доске.
За правильный ответ обучающийся получает 2 жетона, при наличии ошибки – 1 жетон, при неверном ответе – 0 жетонов.
Задача 5:
Колба коническая имеет высоту 185 мм и диаметр 120 мм. Найдите примерный объем колбы. (Принять  Ответ дать в мл и округлить до целого числа, считая что 1 мл = 1000 мм3).
Ответ дать в мл и округлить до целого числа, считая что 1 мл = 1000 мм3).
Решение:
Объем колбы можно найти по формуле:  .
.
Радиус колбы R=D:2. R=120:2=60 (мм).
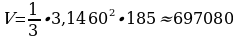 (мм3).
(мм3).
697080 мм3  697 мл.
697 мл.
Ответ: 697 мл.
-
Формула нахождения объема шара.
Вводится формула для вычисления объема шара. В таблице опорного конспекта записывается формула площади сферы и объема шара.
| Площадь | Объем |
| Сфера: S=4R2 | Шар: |
-
Примеры решения задач.
Обучающимся предлагается решить задачу на вычисление объема шара по готовому чертежу.
Обучающийся давший первым правильный ответ записывает решение на доске.
За правильный ответ обучающийся получает 2 жетона, при наличии ошибки – 1 жетон, при неверном ответе – 0 жетонов.
Задача 6: Плечевой сустав ребенка, имеющий форму полушария имеет диаметр 2,2 см. Найдите примерный объем сустава. (Принять  Ответ округлите до одного знака после запятой.).
Ответ округлите до одного знака после запятой.).
Решение:
Объем сустава можно найти по формуле: 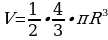 .
.
Радиус сустава R=D:2. R=2,2:2=1,1 (см).
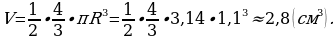
Ответ: 2,8 см3.
Задача 7:
Колба круглодонная имеет диаметр 57,6 мм. Найдите примерный объем колбы. (Принять  Ответ дать в мл и округлить до целого числа, считая что 1 мл = 1000 мм3).
Ответ дать в мл и округлить до целого числа, считая что 1 мл = 1000 мм3).
Решение:
Объем колбы можно найти по формуле:  .
.
Радиус колбы R=D:2. R=57,6:2=28,8 (мм).
 (мм3).
(мм3).
100010 мм3  100 мл.
100 мл.
Ответ: 100 мл.
-
Первичное закрепление (15-20 мин).
Практическая работа в парах (измерение элементов многогранника или тела вращения и вычисление его объема).
Каждой паре обучающихся на парту раздается модель многогранника или тела вращения с указанным номером (номера могут повторяться). Необходимо сделать чертеж, произвести необходимые замеры для вычисления объема (учитывая погрешность измерений округлять до целого числа). Составить задачу и оформить ее решение.
Для решения задачи по каждой из моделей к доске вызывается один обучающийся.
При проверке решение задачи выводится на экран.
За правильный ответ обучающийся получает 2 жетона, при наличии ошибки – 1 жетон, при неверном ответе – 0 жетонов.
Например:
-
Правильная четырехугольная пирамида: высота – 12 см, сторона основания – 10 см.
Задача: Высота правильной четырехугольной пирамиды 12 см, а сторона основания 10 см. Найдите объем пирамиды.
Решение:
Основанием правильной четырехугольной пирамиды является квадрат, т.е. площадь основания можно найти по формуле Sосн=а2.
Тогда объем пирамиды  .
.
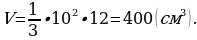
Ответ: 400 см3.
-
Прямая треугольна призма: высота – 8 см, стороны основания – 3 см, 6 см, 7 см.
Задача: Высота прямой треугольной призмы 8 см, а стороны основания – 3 см, 6 см, 7 см. Найдите объем призмы.
Решение:
Основанием прямой треугольной призмы является треугольник, т.е. площадь основания можно найти по формуле S= 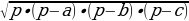 .
. 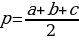 .
.
 S=
S=  (см2).
(см2).
Тогда объем призмы 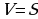
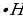 . V=
. V=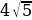 8=
8=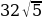 (см3).
(см3).
Ответ: 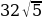 см3.
см3.
-
Цилиндр: высота – 15 см, диаметр – 6 см.
Задача: Найдите объем цилиндра, высота которого составляет 15 см, а радиус основания – 6 см.
Решение: Найдем радиус цилиндра R=D:2. R=6:2=3 (см).
Тогда объем цилиндра найдем по формуле V=R2H. V=3215=135 (см3).
Ответ: 135 см3.
-
Домашнее задание (1-2 мин).
Учить опорный конспект, по учебнику гл. VII § 1-4. Вопросы к главе VII № 3,5,8.
-
Рефлексия и подведение итогов (3-5 мин).
Обучающиеся по кругу высказываются одним предложением, выбирая начало фразы на экране:
Сегодня я узнал…
Было интересно…
Было трудно…
Я выполнял задания…
Я понял, что…
Теперь я могу…
Я почувствовал, что…
Я приобрёл…
Я научился…
У меня получилось…
Я смог…
Я попробую…
Меня удивило…
Урок дал мне для жизни…
Мне захотелось…
Подведение итогов занятия и выставление оценок.
Обучающийся набравший 3 и более жетонов получает оценку «отлично», 2 жетона – «хорошо», 1 жетон – «удовлетворительно».
Список источников
Основные:
-
Атанасян Л.С, Бутузов В.Ф., Кадомцев С.Б. и др. Математика: алгебра и начала математического анализа, геометрия. Геометрия (базовый и углубленный уровень). Просвещение, 2018г.
Дополнительные:
-
Вся элементарная математика: Средняя математическая интернет-школа [Электронный ресурс]. – Режим доступа: http://www.bymath.net.
-
Единая коллекция цифровых образовательных ресурсов [Электронный ресурс]. – Режим доступа: http://www.school-collection.edu.ru.
-
Информационные, тренировочные и контрольные материалы: Федеральный центр информационно-образовательных ресурсов. [Электронный ресурс]. – Режим доступа: http://www.fcior.edu.ru.
-
Математика: учебно-методический журнал для учителей: Издательский дом 1 сентября. [Электронный ресурс]. – Режим доступа: http://mat.1september.ru.
-
Математический портал – образовательные онлайн сервисы по математике, физике, теории вероятности и другим предметам [Электронный ресурс]. – Режим доступа: http://www.webmath.ru.
Приложение 1
Опорный конспект для обучающегося
Теоретический блок
| Площадь | Объем |
| Определение: Площадь многоугольника – это | Определение: Объем тела – это
|
| Единицы измерения: ____________________________________ За единицу измерения площадей берут квадрат, сторона которого равна единице измерения отрезков.
| Единицы измерения: ____________________________________ За единицу измерения объемов принимают куб, ребро которого равно единице измерения отрезков. Куб с ребром 1 см называют кубическим сантиметром и обозначают 1 см3. |
| Свойства:
____________________________________. | Свойства:
_____________________________________ ____________________________________. |
| Равновеликими называются геометрические фигуры, имеющие равные _________________. | Равновеликими называются тела, ______________ которых равны. |
| Площадь основания | Объем |
| Куб: S= | Куб: V= |
| Прямоугольный параллелепипед: S= | Прямоугольный параллелепипед: V= |
| Прямая призма: Формула площади основания прямой призмы зависит от того какая фигура в основании. Например: S= S= S= Sпарал= Sпарал= Sпарал= | Прямая призма: V= |
| Наклонная призма: Формула площади основания наклонной призмы зависит от того какая фигура в основании. | Наклонная призма: V= |
| Пирамида: Формула площади основания пирамиды зависит от того какая фигура в основании. | Пирамида: |
| Конус: S= | Конус: |
| Сфера: S= | Шар: |
Практический блок
Решение задач
Задача 1:
Лоток полимерный прямоугольный с крышкой имеет форму прямоугольного параллелепипеда и размеры 200 мм, 155 мм, 40 мм. Найдите объем лотка. (Ответ дать в литрах, считая что 1л=1000 мл = 1000000 мм3).
| Дано:
Найти:
| Решение:
|
Ответ:
Задача 2:
Тело поджелудочной железы имеет форму приближенную к трёхгранной (треугольной) призме. Предположим, что его длина у человека весом 60 кг составляет 18 мм, а разрез, являющийся основанием призмы, представляет собой треугольник с высотой 7 мм и основанием 8 мм. Найдите примерный объем тела поджелудочной железы.
| Дано:
Найти:
| Решение:
|
Ответ:
Задача 3:
Пробирка для забора крови имеет форму цилиндра с диаметром 16 мм и высотой 100 мм. Какой примерный объем крови сдал пациент, если в пробирку было набрано крови ровно половину возможного объема? (Принять  Ответ дать в мл и округлить до целого числа считая что 1 мл = 1000 мм3).
Ответ дать в мл и округлить до целого числа считая что 1 мл = 1000 мм3).
| Дано:
Найти:
| Решение:
|
Ответ:
Задача 4:
Контейнер для биологического материала имеет размеры внутренний диаметр 38 мм, а высота до резьбы 53 мм. Найдите примерный объем контейнера. (Принять  Ответ дать в мл и округлить до целого числа считая что 1 мл = 1000 мм3).
Ответ дать в мл и округлить до целого числа считая что 1 мл = 1000 мм3).
| Дано:
Найти:
| Решение:
|
Ответ:
Задача 5:
Колба коническая имеет высоту 185 мм и диаметр 120 мм. Найдите примерный объем колбы. (Принять  Ответ дать в мл и округлить до целого числа, считая что 1 мл = 1000 мм3).
Ответ дать в мл и округлить до целого числа, считая что 1 мл = 1000 мм3).
| Дано:
Найти:
| Решение:
|
Ответ:
Задача 6: Плечевой сустав ребенка, имеющий форму полушария имеет диаметр 2,2 см. Найдите примерный объем сустава. (Принять  Ответ округлите до одного знака после запятой).
Ответ округлите до одного знака после запятой).
| Дано:
Найти:
| Решение:
|
Ответ:
Задача 7:
Колба круглодонная имеет диаметр 57,6 мм. Найдите примерный объем колбы. (Принять  Ответ дать в мл и округлить до целого числа, считая что 1 мл = 1000 мм3).
Ответ дать в мл и округлить до целого числа, считая что 1 мл = 1000 мм3).
| Дано:
Найти:
| Решение:
|
Ответ:
Практическая работа
Название многогранника / тела вращения: ___________________________________________
Измерения: __________________________________________________________________
Текст задачи: ____________________________________________________________________
_____________________________________________________________________________
______________________________________________________________________________
____________________________________________________________________________
| Дано:
Найти:
| Чертеж: | Решение:
|
Ответ:

 Получите свидетельство
Получите свидетельство Вход
Вход



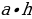
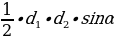











 Объемы многогранников и тел вращения (76.79 KB)
Объемы многогранников и тел вращения (76.79 KB)
 0
0 886
886 26
26 Нравится
0
Нравится
0


