О расстоянии между стратами

О расстоянии между стратами

Суровцева Н.Н., Клейменов В.Ф.

Иркутский национальный исследовательский технический университет,

Иркутск, Россия

При рассмотрении иерархических систем иногда необходимо оценить, насколько две страты близки друг к другу. Для этого вводится понятие расстояния между стратами. Дадим два следующих эквивалентных определения.

Определение 5. Расстоянием d₁ (A,B) между стратами называется число

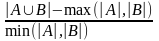d₁ = (1),

где |A|, |B| - мощность страт A и B, min (a,b) – минимальное из чисел a,b, а max (a,b) – максимальное из чисел a,b.

Определение 6.Расстоянием d₂ (A,B) между стратами называется число

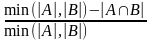d₂ = (2).

Утверждение 3. Расстояния между стратами обладают следующими свойствами:

1. d₁ (A,B)= d₂(A,B)= d(A,B);

2.d(A,B)=1 A∩B= Ø;

3. d(A,B)=0 A B или B A;

4. 0≤ d(A,B)≤1.

Доказательство.

1. Действительно, пусть |A|=m, |B|=n, |A∩B|=r и для определенности m≤n. Тогда |A B|= m+n-r. Вычислим расстояние d₁. По определению 5 получим d₁=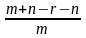 = 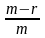, но по определению 6 d₂= 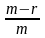. То есть d₁= d₂ и можно обозначить это число через d.

2. Если A∩B= Ø, то r=0 и d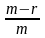 = =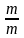 1. Если d= 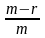=1, то r=0 и A∩B= Ø.

3. Пусть m≤n, тогда, так как d=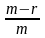 =0, то m=r и (A∩B) A. Отсюда A∩B=A и A B. Обратно, если A B, то A∩B=A, m=r, m-r=0 и d=0.

4. Из формулы d=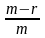 и неравенства r≥0 следует неравенство 0≤d≤1. Утверждение доказано.

Из формул (1) и (2) следует, что чем меньше расстояние d(A,B), тем страты A и B меньше отличаются друг от друга. Для разных иерархических систем бывает удобнее пользоваться либо формулой (1) либо формулой (2).

С помощью понятия расстояния между стратами можно доказать следующий критерий немодулярности.

Утверждение 4. В иерархии I тогда и только тогда существует немодулярная подрешетка, когда в ней найдутся такие страты A, B, C, которые удовлетворяют следующим условиям:

1. d (A,C)=0, A≠C;

2. d (A,B)0;

3. B∩C=A∩B (при этом, если |B|d(A,B)= d(B,C)).

Доказательство. Из условия 1 следует, что A C, а из условия 2 что не выполняются следующие включения: ни A B, ни B A. Докажем теперь замечания из условия 3. Пусть d(A,B)=d(B,C) и |B|A C, то A∩B≤ C∩B. Допустим, что A∩B≠C∩B. Тогда |A∩B|C∩B|, но отсюда min (|A|, |B|)=min(|B|, |C|)=|B|=m₁, то d(A,B)=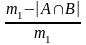 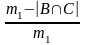=d(B,C), что противоречит замечанию из условия 3. Итак, B∩C= A∩B≠ A.

Рассмотрим теперь подрешетку В С, С, В, А, A∩B, где A∩B≠A по условию 2.

Тогда элементы этой подрешетки удовлетворяют условиям С≥А, В С=А С и А (В С)=А с другой стороны (А В) = (С В) и (А В) С = (С В) С=С, но так как A≠С, то А (В С)≠(А В) С и построенная подрешетка немодулярна.

Пусть теперь, обратно, в иерархии I существует немодулярная подрешетка. Тогда, по теореме 12 из главы 1 монографии [3], в I существует подрешетка N_5, элементы которой удовлетворяют условиям 1, 2, 3. Утверждение доказано.

Список литературы

1. М. Месарович, Д. Мако Д, Такахара И., Теория иерархических многоуровневых систем «Мир», М., 1973г., 344с.

2. Г. Биркгоф., Теория решеток, «Наука», М., 1984г., 566с.

3. Клейменов В.Ф., Суровцева Н.Н., Иерархические системы: расстояния между стратами и факторизация систем// Современные наукоемкие технологии № 11, 2010г., С. 75-77

4. Суровцева Н.Н., Клейменов В.Ф., Динамические иерархические системы в социальной работе // Успехи современного естествознания № 5, 2011г., С. 139-140