Математический институт Клэя — частная некоммерческая организация, расположенная в Кембридже, штат Массачусетс. Был основан в 1998 году бизнесменом по имени Лэндон Клэй и математиком из Гарварда Артуром Джеффи. Цель института — увеличение и распространение математических знаний. С этой целью институт выдаёт различные награды и спонсирует многообещающих математиков.
Институт наиболее известен после объявления 24 мая 2000 года списка Проблем тысячелетия (Millennium Prize Problems). Эти семь проблем определены как «важные классические задачи, решение которых не найдено вот уже в течение многих лет». За решение каждой из задач предложен приз в 1000000 долларов США. Анонсируя приз, институт Клэя провёл параллель со списком проблем Гильберта, представленным в 1900 году и оказавшим существенное влияние на математиков XX века. Из 23 проблем в списке большинство уже решены и только одна — гипотеза Римана, вошла в список института Клэя.
По состоянию на март 2010 года одна из семи проблем тысячелетия (гипотеза Пуанкаре) решена. Премия за доказательство гипотезы Пуанкаре присуждена российскому математику Г. Я. Перельману, опубликовавшему в 2002 году серию работ, доказывающую исходную гипотезу. Однако, Григорий Перельман отказался принять премию и денежный приз, сказав: «У меня есть все, чего я хочу».
Откры́тые (нерешённые) математи́ческие пробле́мы — проблемы, которые рассматривались математиками, но до сих пор не решены. Часто имеют форму гипотез, которые предположительно верны, но нуждаются в доказательстве.
В научном мире популярна практика составления известными учёными или организациями списков открытых проблем, актуальных на текущий момент. В частности, известными списками математических проблем являются:
Проблемы Гильберта
Проблемы Ландау
Проблемы тысячелетия
Проблемы Смейла
Проблемы Ги́льберта — список из 23 кардинальных проблем математики, представленный Давидом Гильбертом на II Международном Конгрессе математиков в Париже в 1900году.
Н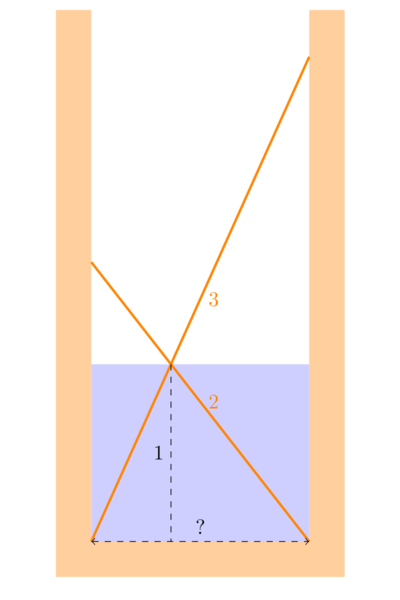 а данный момент решены 16 проблем из 23. Ещё 2 не являются корректными математическими проблемами (одна сформулирована слишком расплывчато, чтобы понять, решена она или нет, другая, далёкая от решения, — физическая, а не математическая). Из оставшихся 5 проблем две не решены никак, а три решены только для некоторых случаев.
а данный момент решены 16 проблем из 23. Ещё 2 не являются корректными математическими проблемами (одна сформулирована слишком расплывчато, чтобы понять, решена она или нет, другая, далёкая от решения, — физическая, а не математическая). Из оставшихся 5 проблем две не решены никак, а три решены только для некоторых случаев.
Неразрешимые задачи древности
Задача Фараона
Квадратура круга
Трисекция угла
Удвоение куба
Задача Фараона или Колодец Лотоса — одна из задач занимательной математики. Задача была сформулирована в 8 веке до н.э. Эта математическая задача — прародитель «неразрешимых задач». В дальнейшем был найден математический метод решения задачи. Ответом является иррациональное алгебраическое число, которое является корнем уравнения 8 степени.
Условие. В круглом колодце налита вода на одну единицу длины. Две разновеликие тростинки, с длиной 2 и 3 единицы соответственно, одними концами упираются в дно колодца, а другими концами опираются на его стены. Тростинки пересекаются на уровне налитой в колодец воды. Какова ширина (диаметр) колодца?
Современная формулировка: На дно колодца опустили две палки длиной 2 м и 3 м так, что они пересекаются. Расстояние от их пересечения до дна составляет 1 м. Найти диаметр основания.
Решение
Задача, несмотря на простую формулировку, точным образом решается сложно.
Легко свести задачу к нахождению положительного корня уравнения ![]() . Далее любой подстановкой, снижающей степень (например,
. Далее любой подстановкой, снижающей степень (например, ![]() ) уравнение преобразуется к уравнению четвёртой степени, которое решается, например, методом Феррари и с помощью формулы Кардано. В итоге получается ответ
) уравнение преобразуется к уравнению четвёртой степени, которое решается, например, методом Феррари и с помощью формулы Кардано. В итоге получается ответ ![]() .
.
Список проблем
| № | Статус | Краткая формулировка | Результат |
| 1 | нет консенсуса | Проблема Кантора о мощности континуума (Континуум-гипотеза) | Неразрешима |
| 2 | нет консенсуса | Непротиворечивость аксиом арифметики. | Требует уточнения формулировки |
| 3 | решена | Равносоставленность равновеликих многогранников | Опровергнута |
| 4 | слишком расплывчатая | Перечислить метрики, в которых прямые являются геодезическими | Требует уточнения формулировки |
| 5 | решена | Все ли непрерывные группы являются группами Ли? | Да |
| 6 | слишком расплывчатая | Математическое изложение аксиом физики |
|
| 7 | решена | Является ли число трансцендентным (или хотя бы иррациональным). | Да |
| 8 | не решена | Проблема простых чисел (гипотеза Римана и проблема Гольдбаха) |
|
| 9 | частично решена | Доказательство наиболее общего закона взаимности в любом числовом поле | Доказана для абелевого случая |
| 10 | решена | Есть ли универсальный алгоритм решения диофантовых уравнений? | Нет |
| 11 | частично решена | Исследование квадратичных форм с произвольными алгебраическими числовыми коэффициентами |
|
| 12 | не решена | Распространение теоремы Кронекера об абелевых полях на произвольную алгебраическую область рациональности |
|
| 13 | решена | Можно ли решить общее уравнение седьмой степени с помощью функций, зависящих только от двух переменных? | Да |
| 14 | решена | Доказательство конечной порождённости алгебры инвариантов линейной алгебраической группы | Опровергнута |
| 15 | частично решена | Строгое обоснование исчислительной геометрии Шуберта |
|
| 16 | частично решена | Топология алгебраических кривых и поверхностей |
|
| 17 | решена | Представимы ли определённые формы в виде суммы квадратов (см. Семнадцатая проблема Гильберта) | Да |
| 18 | решена | Конечно ли число кристаллографических групп? Существуют ли нерегулярные заполнения пространства конгруэнтными многогранниками? Являются ли гексагональная и кубическая гранецентрированная упаковки шаров наиболее плотными? | Да Да Да |
| 19 | решена | Всегда ли решения регулярной вариационной задачи Лагранжа являются аналитическими? | Да |
| 20 | решена | Все ли вариационные задачи с определёнными граничными условиями имеют решения? | Да |
| 21 | решена | Доказательство существования линейных дифференциальных уравнений с заданной группой монодромии | Требует уточнения формулировки |
| 22 | решена | Униформизация аналитических зависимостей с помощью автоморфных функций |
|
| 23 | не решена | Развитие методов вариационного исчисления |
|
Cемь нерешенных математических проблем - "Millennium Prize Problems", за решение каждой из которых будет выплачен $1 млн.
Проблема Кука (сформулирована в 1971г.).
Допустим, находясь в большой компании, Вы хотите убедиться, что там же находится Ваш знакомый. Если Вам скажут, что он сидит в углу, то Вам достаточно доли секунды, чтобы, бросив взгляд, убедиться в истинности информации. В отсутствии этой информации Вы будете вынуждены обойти всю комнату, рассматривая гостей.
Гипотеза Римана (сформулирована в 1859г.).
Некоторые целые числа не могут быть выражены как произведение двух меньших целых чисел, например, 2, 3, 5, 7, и т.д. Такие числа называются простыми числами, и они играют важную роль в чистой математике и ее приложениях. Распределение простых чисел среди всех натуральных чисел не подчиняется никакой закономерности, однако немецкий математик Риман (1826 - 1866) обнаружил, что число простых чисел, не превосходящих x, выражается через распределение нетривиальных нулей дзета-функции Римана. Риман высказал гипотезу, не доказанную и не опровергнутую до сих пор, что все нетривиальные нули дзета-функции лежат на прямой линии. На сегодняшний день проверены первые 1500000000 решений.
Гипотеза Берча и Свиннертон-Дайера.
Математики давно заворожены проблемой описания всех решений в целых числах x, y, z алгебраических уравнений, то есть уравнений от нескольких переменных с целыми коэффициентами. Примером алгебраического уравнения является уравнение x2 + y2 = z2. Евклид дал полное описание решений этого уравнения, но для более сложных уравнений получение решения становится чрезвычайно трудным (например, доказательство отсутствия целых решений уравнения xn + yn = zn ).
Гипотеза Ходжа.
В двадцатом веке математики изобрели мощные методы исследования формы сложных объектов. Основная идея состоит в том, чтобы выяснить, до какой степени мы можем аппроксимировать форму данного объекта, склеивая вместе простые тела возрастающей размерности. Этот метод оказался эффективным при описании разнообразных объектов встречающихся в математике. К сожалению, при этом были не ясны геометрические обоснования метода: в некоторых случаях было необходимо прибавлять части, которые не имели никакого геометрического истолкования.
Уравнения Навье-Стокса.
Если плыть в лодке по озеру, то возникнут волны, а если лететь в самолете - в воздухе возникнут турбулентные потоки. Предполагается, что эти и другие явления описываются уравнениями, известными как уравнения Навье-Стокса. Решения этих уравнений не известны, и при этом даже не известно, как их решать. Необходимо показать, что решение существует и является достаточно гладкой функцией. Решение этой проблемы позволит существенно изменить способы проведения гидро- и аэродинамических расчетов.
Проблема Пуанкаре.
Если натянуть резиновую ленту на яблоко, то можно, медленно перемещая ленту без отрыва от поверхности, сжать ее до точки. С другой стороны, если ту же самую резиновую ленту соответствующим образом натянуть вокруг бублика, то никаким способом невозможно сжать ленту в точку, не разрывая ленту или не ломая бублик. Говорят, что поверхность яблока "односвязна", а поверхность бублика - нет. Пуанкаре почти сто лет назад знал, что в двумерном случае односвязна только сфера, и задался аналогичным вопросом для трехмерной сферы - множества точек в четырехмерном пространстве, равноудаленных от некоторой точки. Доказать, что односвязна только сфера, оказалось настолько трудно, что математики до сих пор ищут ответ.
Уравнения Янга-Миллса.
Уравнения квантовой физики описывают мир элементарных частиц.

 Получите свидетельство
Получите свидетельство Вход
Вход











 Неразрешимые алгоритмические проблемы (159.5 KB)
Неразрешимые алгоритмические проблемы (159.5 KB)
 0
0 322
322 8
8 Нравится
0
Нравится
0







