Необходимый теоретический материал для успешной сдачи ОГЭ-9 по математике для учеников разной подготовленности

Муниципальное бюджетное общеобразовательное учреждение средняя общеобразовательная школа №14 г.Искитима

Необходимый теоретический материал для сдачи ОГЭ по математике.

(краткая теория+ формулы)

Чудинова А.С

Учитель математики

1 квалификационной

категории

2019год

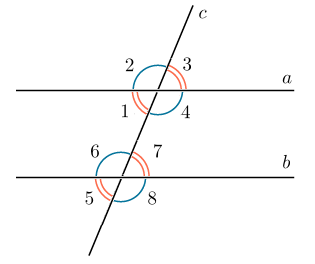
1.Углы:

Вертикальные углы равны (на рис 1и3; 6и8 и др)

Внутренние накрест лежащие углы при параллельных прямых и секущей равны. (на рис 4и6; 1 и 7)

Сумма внутренних односторонних углов при параллельных прямых и секущей равна 180˚( на рис 4 и 7; 1 и6)

Соответственные углы при параллельных прямых и секущей равны.(на рис 3 и 7; 1 и 5 и др)

Если одна из двух параллельных прямых перпендикулярна третьей прямой, то и другая перпендикулярна третьей прямой.

2. Медиана, биссектриса, высота

Биссектриса треугольника — отрезок, соединяющий вершину треугольника с точкой на противоположной стороне и делящий угол треугольника пополам.

Высота треугольника -- перпендикуляр опущенный из вершины угла на противоположную сторону

Медиана треугольника — это отрезок, соединяющий вершину треугольника с серединой противолежащей стороны. 

В любом треугольники все биссектрисы пересекаются в одной точке, все медианы пересекаются в одной точке, все медианы пересекаются в одной точке

3.Треугольник:

Сумма углов в любом треугольнике 180˚

Средняя линия треугольника -- прямая проходящая через середины двух сторон. Средняя линия параллельна одной из сторон и равна половине этой стороны

В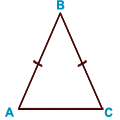 иды треугольников: тупоугольный ( один угол тупой), прямоугольный (один угол прямой 90˚), остроугольный ( все углы острые, меньше 90˚)

Равнобедренный треугольник   —   треугольник  
у которого равны   две стороны. 

Свойства равнобедренного треугольника:  
            в равнобедренном треугольнике углы при основании равны;  

в равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой;  

Р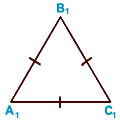 авносторонний треугольник   —   треугольник  
у которого   все стороны   равны.  ( все углы по 60 градусов)

Всякий равносторонний треугольник является равнобедренным,  
но не всякий равнобедренный   —   равносторонним.    

Три признака равенства треугольников

I признак по двум сторонам и углу между ними

II признак (по стороне и прилежащим углам)

III признак (по трем сторонам)

Признаки подобия треугольников

I признак по двум равным углам

II признак по двум пропорциональным сторонам и углу между ними

III признак : по трем пропорциональным сторонам

Площади подобных фигур относятся как коэффициент подобия в квадрате.

Объемы подобных фигур относятся как коэффициент подобия в кубе

Треугольник называется прямоугольным, если один из его углов прямой.

Стороны, прилежащие к прямому углу называются катетами, а сторона, лежащая против прямого угла, – гипотенузой. (самая большая сторона это гипотенуза, две др катеты)

Свойства прямоугольного треугольника:

Сумма острых углов прямоугольного треугольника равна 90 градусов 

Катет, лежащий против угла  в 30˚, равен половине гипотенузы.

Центр описанной окружности прямоугольного треугольника лежит на середине гипотенузы.

Медиана прямоугольного треугольника, проведенная из вершины прямого угла на гипотенузу, является радиусом описанной около этого треугольника окружности:

Теорема Пифагора: 

В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов: a²+b²=c²

Пифагоровы тройки:

3,4,5

6,8,10

5,12,13

9,12,15

Признаки равенства прямоугольных треугольников

По двум катетам: 

По гипотенузе и катету: 

По катету и прилежащему острому углу: 

По катету и противолежащему острому углу

По гипотенузе и острому углу

Признаки подобия прямоугольных треугольников:

По острому углу

По пропорциональности двух катетов

По пропорциональности катета и гипотенузы

Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе

Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе

Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему

Котангенсом острого угла прямоугольного треугольника называется отношение прилежащего катета к противолежащему:

Высота, проведенная из вершины прямого угла, разбивает прямоугольный треугольник на два подобных треугольника. Каждый из этих треугольников подобен исходному: 

Высота прямоугольного треугольника: h=ab/c или h= 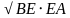( где АВ гипотенуза, СЕ высота опущенная на гипотенузу)

В прямоугольном треугольнике медиана, проведённая из вершины прямого угла, равна половине гипотенузы: m=c/2 (R=​с/2=m​_c)

3. Четырехугольники:

Сумма углов в любом четырехугольнике 360 ˚

П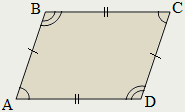 араллелограмм

Параллелограммом называется четырёхугольник, противолежащие стороны которого попарно параллельны:

У параллелограмма противолежащие стороны равны и противолежащие углы равны:

Сумма любых двух соседних углов параллелограмма равна 180°:

Диагонали параллелограмма пересекаются и точкой пересечения делятся пополам:

Каждая диагональ делит параллелограмм на два равных треугольника:

Две диагонали параллелограмма делят его на четыре равновеликих треугольника:

С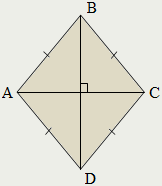 умма квадратов диагоналей параллелограмма равна сумме квадратов всех его сторон

Ромб

Ромбом называется параллелограмм, у которого все стороны равны.

Диагонали ромба пересекаются под прямым углом и являются биссектрисами его углов:

Прямоугольник.

Прямоугольником называется параллелограмм, у которого все углы прямые:

Диагонали прямоугольника равны и точкой пересечения делятся на четыре равных отрезка.

Квадрат.

Квадрат – это прямоугольник, у которого все стороны равны:

Диагонали квадрата равны и перпендикулярны.

С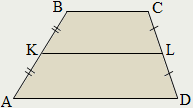 торона и диагональ квадрата связаны соотношениями: d=a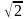

Трапеция.

Трапецией называется четырёхугольник у которого только две противолежащие стороны параллельны:

Параллельные стороны называются основаниями трапеции, непараллельные – боковыми сторонами.

Средняя линия трапеции параллельна её основаниям и равна их полусумме.

Равнобокой называется трапеция, у которой боковые стороны равны:

У равнобокой трапеции: диагонали равны; углы при основании равны; сумма противолежащих углов равна 180.

Стороны и диагональ равнобокой трапеции связаны соотношением:

d² = ab+c².

Т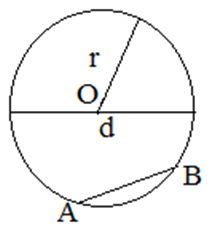 рапеция называется прямоугольной, если одна из её боковых сторон перпендикулярна основаниям.

4. Окружность:

Отрезок, соединяющий центр окружности с любой точкой окружности называется радиусом (r) окружности

Отрезок  , соединяющий две точки окружности, называется хордой. Хорда, проходящая через центр окружности, называется диаметром окружности.

Прямая, имеющая с окружностью одну общую точку, называется касательной. Касательная и радиус проведенный в точку касания пересекаются под прямым углом

Прямая, имеющая с окружностью две общие точки, называется секущей.

Центральный угол окружности – это угол, вершина которого лежит в центре окружности. Центральный угол равен дуге на которую он опирается.

Вписанный угол – это угол, вершина которого лежит на окружности, а стороны пересекают ее. Вписанный угол равен половине дуги на которую опирается.

Через три точки, не лежащие на одной прямой, можно провести окружность, и притом только одну.

Вписанный угол, опирающийся на диаметр равен 90˚.

Все вписанные углы, опирающиеся на одну и туже дугу равны.

Теорема косинусов:

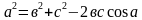
Теорема синусов:

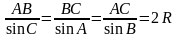
5. Формулы площадей

Треугольник :

S = ½(a ⋅ h_a)

S = ½(ab ⋅ sinC)

S = √p(p - a)(p - b)(p - c)  (р- полупериметр) Формула Герона:

S=1/2(a⋅b) (прямоугольный треугольник, а,b – катеты)

S=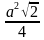 ( равносторонний треугольник)

S=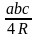 ( R- радиус описанной окружности)

S=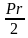 (r – радиус вписанной окружности, P – периметр)

квадрат: S = a ⋅ a = a²

прямоугольник S = a ⋅ b

параллелограмм:

S = a ⋅ h_a

S =ab ⋅ sinC

S=1/2 d₁·d₂· sinC

Ромб : S= d₁·d₂ ·sinC

Трапеция :S=1/2(a+b)⋅h (а, b основания трапеции)

Круг: S=π⋅r²

задание: теория вероятности.

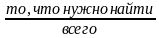
Ответ не может быть больше 1

задание:

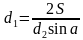
Формулы сокращенного умножения:

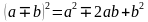
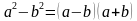
Признаки делимости ( необходимо для сокращения и подбора нового знаменателя)

Признак делимости на 2

Последняя цифра числа должна быть четной - 0,2,4,6,8

Признак делимости на 3

Сумма цифр в данном числе должна быть кратна 3

Признаки делимости на 5

Последняя цифра должна быть 0 или 5

Признак делимости на 9

Сумма цифр в данном числе должна быть кратна 9

Признак делимости на 10

Последняя цифра должна быть 0

Разделить на 10, 100, 1000 и т.д, значит перенести запятую на столько знаков влево, сколько нулей в делителе (пример 256:10000=0,0256; 3,7:10=0,37)

Свойства степеней

 aⁿ • a^k   =   a^n+k  

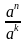   =   a^n−k   или   aⁿ : a^k = a^n−k    

 a⁰ =1 

 (aⁿ)^k   =   a^nk  

a^m × b^m = (ab)^m
a^m ÷ b^m=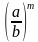 

Стандартный вид числа: записать число цифрами, поставить запятую после первого числа, сосчитать количество цифр после запятой и записать 10 в той степени сколько цифр после запятой.

Пример: 173 тыс= 173000=1,73·105

Любое квадратное уравнение ( степень у икса 2) можно решить через дискриминант (D= b²-4ac, x_1,2= )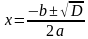

Теорема Виета (применяется когда коэффициент а =1) :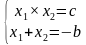

Неполные квадратные уравнения:

1 вид:

ax²+bx=0 – неполное квадратное уравнение (с=0).

Решение: x (ax+b)=0 

x₁=0 или ax+b=0 

x₂=-b/a. 

Ответ: 0; -b/a.

2 вид:

ax²-c=0 – неполное квадратное уравнение (b=0);

Решение: ax²=c 

x²=c/a.

Если (c/a)

Если (с/а)0, то имеем два действительных корня: x₁=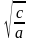 x₂= -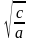

Неравенства:

Линейные неравенства решение:

1.с неизвестным в одну сторону, число в др. знак неравенства сохраняется.

Знак неравенства меняется, если делим обе части неравенства на отрицательное число.

2.чертим координатную прямую, отмечаем точки в порядке возрастания. Точки пустые если знак неравенства , точки жирные если знак неравенства , заштриховываем нужные ответ по знаку неравенства.

3.Записываем ответ. Если точка пустая или бесконечность -- скобки круглые, точка жирная -- скобка квадратная.

Квадратные неравенства:

1. Переписываем уравнение, заменяя знак неравенства на знак равно.

2. Решаем квадратное уравнение любым известным способом.

3. На координатной прямой расставляем точки в порядке возрастания (пустые или жирные)

4. В любом из полученных интервалов берем любую удобную для счета точку, подставляем в уравнение, в правой части которого 0,

5. Определяем знак на промежутке. Расставляем знаки на оставшихся интервалах.

6. Выбираем нужный соответствовав знаку неравенства

7. Записываем ответ. Если точка пустая или бесконечность -- скобки круглые, точка жирная -- скобка квадратная.

Решение системы неравенств:

1. Решаем отдельно первое неравенство из системы.

2. Решаем отдельно второе неравенство из системы.

3. На одной координатной прямой отмечаем получившиеся точки из первого и второго решения в порядке возрастания.

4. Согласна знаку неравенства сверху штрихуем решение первого неравенства, решение второго неравенства.

5. Там где штриховка совпала (снизу и сверху) есть решение всей системы неравенств. Если совпадений нет, то решений системы нет)