Орієнтовний план проведення тижня математики
|
| Дата | Назва заходу | Учасники |
| День 1й |
| Урочиста лінійка “Серед усіх наук, що відкривають шлях до пізнання законів природи, найвеличнішою є математика” (С. Ковалевська). Конкурс математичних газет та мультимедійних презентацій. Перший тур шкільної олімпіади. | 5-11 класи
5-11 класи 5-11 класи |
| День 2й |
| Уроки самоврядування учнями 9-11 класів для 1-4 класів. Виховний захід для 6-их класів “Математичні розваги. Позакласний захід для 7-их класів “Математична казка на новий лад” з використанням мультимедійних технологій. | 9-11 класи
6 класи
7 класи |
| День 3й |
| Гра “Міс Математика. Змагання юних математиків. Другий тур шкільної олімпіади. | 7 класи 8 класи |
| День 4й |
| Математичне кафе для учнів 8 класів Без математики нині, як без рук (КВК між командами 10 класу). | 8 класи 10 класи |
| День 5й |
| Внесок українських вчених у розвиток математики. Лінійка “Підведення підсумків тижня математики”. Анкетування учнів. | 9-11 класи 5-11 класи
5-11 класи |
День 1й
Урочиста лінійка “Серед усіх наук, що відкривають шлях до пізнання законів природи, найвеличнішою є математика” (С. Ковалевська).
Конкурс математичних газет та мультимедійних презентацій.
Розділити учнів на бригади. Бригади, що готують газети та бригади, що готують мультимедійні презентації.
3. Перший тур шкільної олімпіади.
Проведення шкільної математичної олімпіади є підведення підсумків роботи вчителів і учнів з розв’язання задач. Ця робота може бути організована так. Про початок олімпіади оголошується по шкільному радіовузлу, випускається спеціальна газета, вивішується оголошення. Для першого туру пропонуються задачі ускладненого шкільного рівня і задачі цікавої математики. Тексти їх поміщаються в математичній газеті або на дошці оголошень під рубрикою “Увага! Готуємось до шкільної математичної олімпіади”. Тут же міститься скринька для розв’язань. Про підготовку до олімпіади оголошують учителі по класах, зачитують умови задач. Задачі пропонуються учням кожного класу, вказується термін, до якого треба подати розв’язання задач. Для розв’язання задач дається до 10 днів.
У наступній газеті оголошується переможці першого туру, кількість балів набраних учасниками, дається правильне розв’язання задач першого туру та умови задач другого туру. Задачі другого туру трохи складніші, одну задачу варто запропонувати складну.
Переможці олімпіади стають учасниками очної заключної математичної олімпіади.
Результати олімпіади, її переможці повинні бути відомі в школі, широко розрекламовані через шкільний радіовузол, шкільну пресу, урочисто нагороджені.
День 2й
Уроки самоврядування учнями 9-11 класів для 1-4 класів.
Виховний захід для 6-их класів “Математичні розваги.
Позакласний захід для 7-их класів “Математична казка на новий лад” з використанням мультимедійних технологій.(див додаток CD диск)
Уроки самоврядування учнями 9-11 класів для 1-4 класів.
Урок 1
Тема: Математика і весна
Мета: Виявити у дітей здатність аналізувати і діяти, визначати форму предмета і зіставляти її з геометричними фігурами. Познайомити дітей з народними прислів’ями та приказками, в яких використовуються числа. Закріпити знання про весну і весняні явища, місяці, цифри, величину. Виховувати інтереси до математики.
Матеріал. Геометричні фігури різної величини, цифри, малюнок кролика.
Хід заняття
Діти сидять на килимі.
Вихователь. Щойно ми отримали листа із запрошенням на свято. Але щоб знати, хто нас запросив на свято, треба відгадати загадку.
Ви у зелені довкола – пасовище, ліс і поле.
Мчать струмочки до ріки, ліплять гнізда ластівки,
І в сороки новина – облітає всіх вона.
Сповіщаючи ...
Діти. Весна!
Вихователь. Після якої пори року і перед якою настає весна?
Діти. Після зими і перед літом!
Вихователь. Весна пише, що має трьох синів. Відгадайте, хто вони?
Ще вітер зимовий з дощем загуде,
Ще сніг острівками лежить де-не-де
Береза сережки свої розпускає
Чи ви здогадались, коли це буває?
Діти. У березні!
Вихователь. Правильно, у березні. Слухайте далі.
Пташки повертаються в рідний край.
Про весну співають, про поле і гай,
Ніжаться на сонці трави і квіти –
То настав ласкавий місяць.
Діти. Квітень!
Вихователь.
А в цім місяці підряд
Маємо багато свят.
Зеленіють буйно трави –
То іде веселий ...
Діти. Травень!
Вихователь. Отже, хто сини у весни?
Діти. Березень, Квітень, Травень!
Вихователь. Крім нас Весна запросила на свято ще гостей. От послухайте. Не людина, а в хатці живе. Хто це? Що за птах?
Діти. Шпак.
Вихователь. А коли прилітають шпаки?
Діти. Навесні.
Вихователь. Давайте побудуємо для шпаків хатинку.
Діти підходять до столів, вибирають потрібні геометричні фігури і викладають “шпаківні”. Вихователь показує дітям малюнок кролика.
Вихователь. А ось ще один гість Весни. Хто це надіслав свій портрет?
Діти. Кролик.
Вихователь. З якого мультфільму цей персонаж?
Діти. з мультфільму про Вінні-Пуха!
Вихователь. Які цифри використав Кролик, щоб намалювати свій портрет?
Діти. 8, 5, 3, 6, 9, 7.
Вихователь. А яку цифру нагадують вуха Кролика?
Діти. Одиницю!
Вихователь. Молодець Кролик, що так дотепно виконав свій портрет! А зараз послухайте народні прислів’я і скажіть, чи використані в них числа.
Один в полі – не воїн.
В роботі – ох! А їсть за трьох.
День гуляє, три – слабий, а на п’ятий вихідний.
Краще на п’ять хвилин раніше, ніж на хвилину пізніше.
Зробив, як Хома на качалках: одну продав, а дев’ять на плечах баби побили!
Відповіді дітей.
Вихователь. Ще один гість запрошений до Весни. Чи вгадаєте?
Які ноги – такий ніс,
По болоту ходить скрізь.
Хату він на хаті має,
Жабам він рахунок знає.
Хто це?
Діти. Лелека!
Вихователь. А які у Лелеки ноги і ніс?
Діти. Довгі!
Вихователь. А тепер порахуйте, скільки жаб піймав Лелека!
Діти рахують, скільки раз вихователь вдарив деревяними поличками і піднімають відповідну цифру.
Вихователь. А тепер скажіть, кого Весна запросила першого на свято? Кого другого? Кого третього? Кого четвертого?
Відповіді дітей.
Заняття закінчується грою “Лелеки і жаби”.
Урок 2
Тема: Математика і звірі
Мета: Навчати дітей відповідати на запитання. Вправляти у відмінюванні іменників в однині та множині, у правильному узгодженні числівника з іменником. Вчити складати поширені речення. Збагачувати словник словами, що означають назви свійських пташок. Закріпити актуалізацію звуків К, Д, П, виробляти силу голосу. Розвивати уважність, кмітливість. Виховувати бажання доглядати за свійськими птахами.
Матеріал. Загадки, макет ставка з кладкою, качка з каченятами, вірші, пісня, програвач, будиночки.
Хід заняття
Вихователь. Добрий день, діти! Хто з вас зможе відгадати загадку? Плавала, купалася, сухою зосталася. Хто це?
Діти. Качка.
Вихователь. Вірно, діти, це качка. Давайте підемо до ставка. Який гарний ставочок! Сюди дуже часто приходять качки, гуси. Послухайте і відгадайте, хто ж це йде до ставка?
У фонограмі запис голосу качки: “Кря-кря-кря”.
Діти. Качка!
В руках у вихователя іграшка-качка.
Вихователь. Качки прийшла купатися. То що вона робить?
Діти. Плаває, купається!
Вихователь. Качечка покупалась, вийшла з води і пішла на кладочку на сонечку погрітись.
В руках у вихователя іграшка – каченятко.
Вихователь. Ще хтось біжить до кладки. Хто це?
Діти. Маленьке каченятко!
Вихователь. Каченя сіло на кладці біля качки. Хто тепер сидить на кладці?
Діти. Качка і каченя!
Вихователь. Хтось знову іде до ставка.
Вихователь ставить на кладку ще одну іграшку – дорослу качку.
Вихователь. Кого ви тепер бачите на кладці?
Діти. Двох качок і одне каченя.
Вихователь. А кого більше? Качок чи каченят?
Діти. Качок! Качок дві, а каченятко одне.
Вихователь. А що треба зробити, щоб качок і каченят було порівну?
Діти. Треба, щоб припливло ще одне каченя.
Вихователь. То давайте покличемо його. Як качечка кличе каченят?
Діти. Кря-кря-кря!
Вихователь. А каченятко, як відповість?
Діти. Кря-кря-кря!
Вихователь. А яким голосом?
Діти. Тихеньким, тоненьким.
Діти імітують то качку, то каченят. В руках у вихователя іграшка каченяти.
Вихователь. Скільки тепер каченят і скільки качок?
Діти. Дві качки і двоє каченят!
Вихователь. Одне каченя пішло у воду. Хто залишився на кладці? Кого більше?
Діти. Більше качок. Їх дві, а каченят одне.
Вихователь забирає з кладки качку.
Вихователь. Кого не стало на кладці?
Діти. Качки.
Вихователь. Чим вкриті качки?
Діти. Пір’ям.
Вихователь. А що їдять?
Діти. Ряску, травичку, рибок, водяних комах.
Вихователь. А ж ось прибігла лисичка. Качки злякались і кинулись у воду. Лисичка побігла по бережку, походила по кладці, та й побігла в лісок. Вона ж води боїться! А качки покупалися, поплавали, та й пішли додому. А ви хочете поплавати як качечки?
Фізкультхвилинка. Діти під музику імітують качечок, “плавають”.
На зелений бережок. Наш гусак піднявсь на кладчку.
Став, як завжди, на зарядку, повернувся вліво, вправо,
Чітко роблять вільні вправи. От зробив гусак зарядку
Та й на річку бух із кладки!
Каже качка: “Так-так-так! Фізкультурник наш гусак!”
Вихователь. А тепер послухайте віршики Грицька Бойка про птахів. Вірш “Качечка”
Качечка кряче – каченят не баче,
Кличе качечка курчат: - Чи не бачили качат?
А це вірш “Гуси-гусенята”
Гуси-гусенята на ніжки одягли червоні панчішки,
І пішли рядком свіжої водиці попити.
Напились води гусенята. Почали купатись, пірнати.
Давайте разом заспіваємо пісеньку про качечку.
Качечка йде, каченят веде,
На попас очку, на холодну водицю,
На зелену травицю.
Діти співають пісню.
Вихователь. А тепер пройдемось, побачимо, хто в будиночках живе.
Дитяча гра “Хто в будиночку живе”.
Діти імітують птахів, курей, курчат.
Вихователь. Зараз ми послухаємо пісеньку А.Лазаренко “Качака”, а потім потанцюємо під музику М.Красєв “Водичка”.
Урок 3
Тема: Математичний турнір
Мета: виявити найактивнішого і найкмітливішого математика в групі. Повторити вивчений матеріал. Удосконалювати обчислювальні навички дітей в межах 10 (на вивченні випадки додавання і віднімання). Розвивати логічне мислення, увагу, пізнавальний інтерес. Виховувати інтерес до книги, колективізм.
Обладнання: “Учні лісової школи з цифрами”, таблиці для усного рахунку, матеріал для індивідуальної роботи. Фланелограф, малюнки до задач, сигнальні картки з цифрами, кадр діафільму “Від одного до десяти”; запис на магнітофоні фізкультхвилинок з числовим змістом.
Хід заняття
(До залу під музику заходять учасники двох команд).
Вихователь. Сьогодні ми проведемо турнір-змагання двох команд: “Плюс” і “Мінус”, для виявлення найуважнішого, найактивнішого та найкмітливішого гравця. (Присутні гості, члени журі, які підведуть підсумок в кінці турніру і виявлять переможців).
1. Завдання. Гра “Рахуй далі”.
Дитина однієї команди починає, а іншої продовжує (ланцюжком)
Рахуємо по порядку через 1.
Рахуємо ланцюжком порядковим номером.
Називаємо числа від 10 в зворотному порядку.
2. Завдання. Гра “Назви сусідів числа”. Вихователь демонструє “звірят лісової школи”, які принесли числа.
Назви попереднє число 6, 10.
Назви наступне число 7, 9.
Порівняй числа 6 і 9, 4 і 7.
3. Завдання. Робота за таблицями:
Гра “Мовчанка”
6 + 3 = ?
8 – 4 = ?
7 + 3 = ?
5 – 2 = ?
Гра “Хто уважніший?”.
Діти заплющують очі. Вихователь олівцем вистукує число, та називає дію – додавання чи віднімання – і знову вистукує число. Діти піднімають голови і сигнальними картками показують відповідь.
Гра “День і ніч”
Ніч. Діти заплющили очі, а вихователь коментує: 6 + 2 + 2 = ?; 6 – 4 + 3 = ?
День. Діти піднімають голови і відповідають.
4. Завдання. Гра “Прапорець переможця”.
На плакаті записані приклади у вигляді сходинок. На верхній сходинці прикріплено прапорець, а на бічних “сходинках” – приклади.
Від кожної команди по черзі гравці розв’язують приклади.
Виграє команда, яка жодного разу не помилилась і першою забере прапорець.
Завдання. Заселити будиночок з числом 10.
а) Поселити числа на поверхах зі складом числа 10.

б) “Щоб на новосілля був швидше чай готовим – накрити чайник кришечками” (вирахувати приклад на чайнику, накрити кришечкою з правильною відповіддю).
в) “Налити в чашку чаю” (Вирахувати приклад на чашечці і підставити блюдце з правильною відповіддю).
г) “Визволити півника, який попав у небезпеку”.
Його лисичка кинула у клітку і зв’язала лапки. Лапки зв’язані стрічками, на яких написані приклади. Розв’язавши приклади – розв’яжем лампки, визволимо півника.
д) “Щоб у нас був хороший настрій – поставимо квіти у вазу”. Розв’язати приклади на тюльпанах.
6. Завдання. (Для капітанів команд).
Гра “Цифри вийшли погуляти”
5, 9, 7, 3, 2
Хто швидше з капітанів складе:
а) ряд чисел в порядку зростання;
б) хто більше з даних чисел складе прикладів.
7. Завдання. Розв’язання задач на кмітливість.
а) Ішов їжачок, знайшов бурячок, знайшов ще 6. Три з них сім’я з’їсть. Скільки залишиться?
(1 + 6 = 7, 7 – 3 = 4).
б) Мій приятель йшов, п’ятака знайшов. Удвох підем – скільки знайдем?
(5 + 5 = 10).
8. Завдання. Геометричний матеріал.
У кожної дитини карта з наклеєними на ній геометричними фігурами. За завданням вихователя кожна дитина повинна стрілкою показати названу фігуру.
Назвати з яких фігур побудована ракета, сонце?
Гра “Зайвий предмет”, “Якої фігури не вистачає?” з геометричним змістом.
Підведення підсумків. Визначення переможця математичного турніру.
Урок 3
Тема: Математичні розваги.
Мета: Виховувати у дітей зацікавленість до математичних завдань, зацікавити їх дотепними іграми, логічними задачами з елементами гумору, викликати радість пізнання.
В зал заходять діти – цифри від 1 до 9, а за ними – решта дітей групи. Кожна цифра характеризує саму себе.
Кругла, наче буква О,
Цифра “нуль”, або ніщо
Як стоїть він сам-саміський,
То й не значить нічогісько!
Далі діти читають вірші С.М.Маршака у перекладі Наталі Забіли.
Вихователь: Діти, а якої цифри у нас нема? Зараз нам про це цифри самі розкажуть.
Гра-драматизація “Десятка”, дійові особи якої Автор, Нуль і Одиниця.
Автор: Веселий нуль прошепотів
Сусідці одиниці.
Нуль: З тобою поруч я б хотів
постояти, сестрице.
Автор: Та одиниця каже
Одиниця: Ти, Нуль, число нікчемне!
Не стій зі мною, бо мені
Це зовсім неприємно!
Автор: А Нуль на це.
Нуль: Я знаю сам
Та якби поруч стати нам
Десятка б з тебе стала!
Поглянь на себе: ти ж у нас
Мала та худорлява!
А станеш більша в десять раз.
Коли я стану справа!
Нехай не кажуть, що нулі
Такі нікчемні і малі.
(Десятка займає своє місце в натуральному ряді чисел).
Вихователь: Всі зібрались цифри в ряд,
Є у нас й Десятка.
В гості тут до нас прийшла
Математика-загадка.
Заходить помічник вихователя – Математика-загадка.
Математика. Добрий день, діти. Я хочу дізнатися, як ви умієте рахувати. Слухайте мої завдання!
Водить діточок завжди Гуска-мата до води,
По стежині до ставочка лопотять вони шнурочком.
А гусак по саду йде і рахунок всім веде
Скільки пальців на руках, стільки діток в гусака.
Скільки ж діток в гусака?
Діти: Десятеро!
Математика: Вірно, діти! Слухайте наступне завдання.
П’ять пар у колі круг ялинки
А ми спитаємо Маринку,
Чи знає скільки танцюристів
Кружляє у вогнях барвистих?
Маринка. Десятеро танцюристів!
Математика. Молодець, Маринко! І останнє завдання слухайте уважно.
Двоє курчаток стоять.
Двоє в шкарлупках сидять.
Шість під крилом у мами-квочки.
Поміркуйте дітки трошки, і скажіть ви нам відразу,
Скільки всіх курчаток разом?
Діти: Десятеро курчаток!
Математика: Молодці ви, діти! Добре вмієте рахувати. А гратися ви вмієте?
Вибирають дві групки дітей по три дитини. Дидактичні ігри: “Хто перший складе 10” (з двох менших чисел). “Доміно” (відібрати кісточки, що в сумі складають 10), “Знайди подарунок” (орієнтування в просторі, рахунок кроків на 10).
Математика: У мене є ще одне цікаве завдання, але воно складне. Будете його виконувати?
Діти: Будемо!
Математика розкладає на столі малюнки.
- Я принесла з собою казкових героїв. Завдання таке: треба вибрати героїв однієї казки. Ця казка вам добре відома. Між іншим, героїв десятеро.
Діти виконують завдання математики
Математика: Тепер ви напевне знаєте, що це за казка. Вона називається...
Діти: “Коза-дереза”.
Математика. А тепер розкладіть малюнки героїв казки в такому порядку, в якому вони з’являються у казці. Хто з них з’являється десятим?
Відповіді дітей.
Математика: Ще я вам розкажу одну історію.
Математика розказує оповідання М.Коцюбинського “Десять розбійників”.
Математика: Так які ж робітники в Одарки?
Відповіді дітей.
Математика: І останнє моє завдання. Послухайте вірш Наталі Забіли “Десять яблучок”.
Ми з дідом коло яблуньок
Ходили день при дні
І вже поспіли яблучка
Солодкі, запашні.
От якось десять малюків
Повз нас до лісу йшли,
І в ручках десять козубків
Усі вони несли.
Сказав дідусь: “Онучку мій, Поклич-но їх сюди.
Візьми ці десять яблучок
Та всім і поклади!”
Ну, я й поклав, як дід казав
Зосталось в мене три...
- Що ж ти зробив? Не наділив
Когось із дітвори?
Яку помилку зробив хлопчки? Не доведете? Ще раз прочитаю, слухайте уважно: Візьми ці десять яблучок і ВСІМ їм поклади”.
А що подумав хлопчик, хто скаже?
Діти: Хлопчик подумав, що по одному яблучку треба покласти в сім козубків!
Математика: Молодці діти! Так і закінчується цей вірш:
було в них десять козубків.
А я ж поклав у СІМ...
Ти так сказав і я не знав,
що треба класти ВСІМ!
Ви – гарні математики! Ви такі кмітливі, уважні, що я до вас ще прийду. Чекайте на мене!
До побачення!
Виховний захід з математики у 6 - их класах
"Математичні розваги"
" Якщо ми дійсно щось знаємо,
то ми знаємо це завдяки математиці."
П. Гассенді
Мета заходу. Зацікавити учнів, розвити навички математичного та логічного мислення, розширити кругозір учнів, пробудити бажання займатися вивченням однієї з найцікавіших наук.
План заходу
1. Вступне слово вчителя.
Тим, хто хоч раз випробував радісне почуття від розв'язку складної задачи, пізнав радість нехай маленького, але відкриття, а кожна задача в математиці - це проблема, до розв'язку якої людство ішло порою довгі роки, - той буде намагатися пізнати іще та використати отримані знання у житті.
Сьогодні ми вітаємо тих , хто пройшов серйозні випробування з математики за межами шкільного уроку, а саме тих, хто прийняв активну участь у Міжнародному конкурсі Кенгуру (називаємо імена учасників минулого року), також вітаємо 10 найкращих учасників шкільної математичної олімпіади, нагороджуємо учасників ІІ етапу ( районного) олімпіади з математики, наймолодшими учасниками якої були учні 6 -их класів.
(Проходить нагородження та вітання учасників і переможців)
2. Основна частина
Представляється журі, що оцінює інсценівки математичних задач від кожного класу; розв'язки математичних тестів командами 6а, 6б, 6в, 6г, 6д .
Між виступами учасників, бажаючи, поза конкурсом, виконують танцювальні номери, співи, сценки, акробатичний номер тощо ( Кожний з виступів коментує глядач, або виконавець з математичної точки зору. За це виконавці можуть одержати приз глядацьких симпатій.)
3. Гра з вболівальниками" Відгадай слово"
4. Оголошення переможців. Нагородження.
Додаток:
1. Задача 1. Золото царя Додона
Шість розбійників обікрали царя Додона. Здобич була багатою. Менше ніж 100 однакових злитків. Почали розбійники ділити здобич, але один злиток виявився зайвим. Розбійники почали сваритися, та в бійці одного розбійника вбили. Знову стали ділити золото, але знову один злиток виявився зайвим. Знову в бійці згинув один розбійник. Так було доти , доки в решті решт залишився тільки один розбійник, який також помер від ран. Скільки злитків було?
___________________________________________________________________
Якщо спочатку було б на один злиток менше, то поділ відбувся.
Число, менше за сто, що ділиться на 2, 3,4,5,6,- це 60.
Усього було 60 + 1 злиток.
2. Задача 2. Суд Париса
Богині Гера, Афродіта, Афіна прийшли до юного Париса, щоб дізнатися, хто з них прекрасніше.
Представ перед Парисом Богині висловили наступні твердження:
Афродіта: Я найкрасивіша. (1)
Афіна: Афродіта не є найкрасивішою. (2)
Гера: Я найкрасивіша. (3)
Афродіта: Гера не є найкрасивішою. (4)
Афіна: Я найкрасивіша. (5)
Парис, що приліг відпочити на краю дороги, не мав за потрібне навіть зняти хустку, якою прикрив очі від яркого сонця. Але богині були наполегливі, і йому обов'язково треба було вирішити, хто з них найпрекрасніша.
Парис мав на думці, що всі твердження найкрасивішої богині істинні, а всі твердження інших богинь хибні.
Чи міг Парис, виходячи з свого твердження, винести те рішення, Що очікували від нього богині, і, якщо міг, то хто є найкрасивішою із богинь?
Парис міг міркувати наступним чином:
А). Припустимо, що Афіна найкрасивіша, тоді твердження (4) є істина. Протиріччя - Гера не є найкрасивішою
Б). Припустимо, що Гера найкрасивіша, тоді твердження (2) є істина. . Протиріччя - Афродіта не є найкрасивішою.
В). Припустимо, що Афродіта найкрасивіша, тоді протиріч немає. Афродіта дійсно найкрасивіша.
Довідка . Парис, в грецькій міфологій син царя Трої Приама. Зевс доручив Парису розсудити між собою ведучих між собою спір про красоту богинь Афіну, Афродіту і Геру. Признав переможницею спору Афродіту , він забезпечив собі її підтримкою під час пограбування жени царя Спарти Менелая - прекрасної Олени, але викликав ненависть інших богинь, які вплинули на падіння Трої в війні, що розпочалась.
3. Задача 3. Легенда о шахматах
Один мудрець придумав гру, яку ми зараз називаємо "шахмати" Пояснив він шаху правила гри. Шаху гра дуже сподобалась і він вирішив щедро нагородити мудреця.
Мудрець не просив ні золота ні срібла, а тільки побажав ,щоб на першу клітину шахматної дошки поклали одне зерно, на друга - два зерна, на третю - чотири зерна і так до 64 клітини, постійно подвіючи число зерен попередньої клітини. шах не зміг повністю виконати умови мудреця, бо
результатом обчислень стало число 18 446 774 073 709 551 615.
Якщо 10 зерен важать один грам, то мудрецю треба було віддати 184 млрд. 467 млн. 440 тис. 737 т 95 кг та 516г пшениці. Якщо на усій Землі за рік вирощують 2 млрд. т, то щоб віддати йому все зерно, його треба вирощувати 92 роки.
Індуський цар Шерам (індійський принц Сирем) навчився грати в шахмати та пізнав в Якщо б царю вдалося засіяти пшеницею всю поверхню Землі, враховуючи моря і океани, гори і пустелі, Антарктиду та Арктику, та отримати задовільний врожай, то можливо років за п'ять він зміг би розрахуватися. (Архімед)
4. Задача 4. Мужик і купець
Одного разу на базарі купець зустрів мужика та склав з ним одну угоду:Кожного дня мужик буде приносити купцю по 100 000 рублів, а купець буде йому віддавати в перший день 1 копійку, в другий - 4 копійки, і так цілий місяць.
Кожного дня мужик приносив по 100 000 рублів та забирав свої копійки. Спочатку купець радів, і не замислювався скільки він віддасть мужику.
На 24 -й день він віддав 83 000, а на 25 -й - 166000, а на 27-й - 671000 рублів.
Таким чином мужик віддав купцю усього 3 млн., а отримав 10 млн. рублів.
5. Задача 5. Задача Піфагора
Якось Полікарт (тиран з острова Самос) під час відвідин Піфагора запитав, скільки в нього учнів. " З радістю скажу тобі, о Полікрате, - відповів Піфагор. - Половина моїх учнів вивчає прекрасну математику, четвертина досліджує таємниці вічної природи, сьома частина вправляється силою... .Додай ще до них трьох юнаків, з яких Теон має найкращі здібності. Стільки учнів веду я до розуміння вічної істини?".
( 1- 1/2 -1/4-1/7 =3/28; 3:3/28 = 28)
28- єдине досконале двозначне число, тобто сума всіх його дільників без самого числа дорівнює досконалому числу. 28 = 1+2+4+7+14
Довідка. У Римі в 1917 році було відкрито дивовижну споруду: навколо невеликого центрального залу було розміщено 28 келій. Це була будівля неопіфогорейської академії наук. У ній було 28 членів. До останнього часу стільки ж членів просто за традицією, входило до складу багатьох вчених товариств.
6. Виступ учасниці концерту.
Зв'язок математики і музики відом з найдавніших часів. В середньовіччі музика навіть займала місце своєрідної математичної дисципліни.
Музику і математику об'єднують красота.
І музика і математика включають в себе рахунок і абстрактну систему означень. Це 7 нот, музичний розмір. В танці це лінія танцю, його фігури, ритм.
Ми представляємо танець корінного населення Північної та Південної Америки, близький родич рок-н-ролу.
7. Гра з вболівальниками" Відгадай слово.
Ведучий.
В давнину вчення про це математичне поняття було у великій шані у піфагорійців. З ним вони пов'язували думки про порядок і красу у природі, про співзвучні акорди в музиці та гармонію у Всесвіті.
Це математичне поняття застосовувалось та застосовується не тільки в математиці, але і в архітектурі, мистецтві. Воно є умовою правильної, наочної та красивої побудови або зображення.
Сучасний запис означення цього поняття був введений видатним німецьким математиком ХVII в. Готфрідом Вільгельмом Лейбніцем.
В 19 - му реченні VII книги Евклід доводить основну властивість цього математичного поняття.
Його використовували та використовують для розв'язку різних задач в давнину, в середні віки, легко і швидко з його допомогою розв'язують задачи і в наш час.
Про яке математичне поняття йде мова?
Дозволяється назвати чотири букви. На обдумування дається одна хвилина.
8. Тест для команд.
| № | Зміст запитання | Відповідь/(правильна відповідь) | Кількість балів |
| 1 | Скільки натуральних дільників має просте число? | (2) | 1 |
| 2 | Яке число є оберненим до 7? | (1/7) | 1 |
| 3 | Напишіть всі дільники числа 12 | (1,2,3,4,6,12) | 2 |
| 4 | Округліть число 0,0278 з точністю до тисячних | (0,028) | 1 |
| 5 | Обчисліть значення виразу 4/100 +7/1000 | (47/1000 або 0,047) | 2 |
| 6 | Товар коштує 60 грн.. Через деякий час його ціна знизилась на 40%. Визначте нову ціну товару. | ( 36 грн. ) | 2 |
| 7 | Яка найменша кількість 3-літрових банок потрібна, щоб розлити 32 літри молока? | (11) | 2 |
| 8 | Яка з наведених дробів є найбільшою: А)7/8 Б) 66/77 В) 555/666 Г) 4444/5555 | ( А) | 4 |
| 9 | Знайдіть корінь рівняння 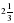 х = х = 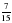
| (1/5) | 2 |
| 10 | Укажіть НСК ( 21; 35 ) | (105) | 3 |
| 11 | Олена може наліпити певну кількість вареників за 4 години, а Марія за 2 години. За який час вони наліплять цю кількість вареників , працюючи разом? | (4/3= 1год20 хв.) (1-вся робота. 1/4+1/2=3/4 1/(3/4)=4/3) | 4 |
| 12 | Зелений, жовтий, червоний кольори світлофора горять послідовно відповідно 50 с., 5 с. 20с.. У деякий момент часу загорілося зелене світло. Яке світло буде горіти через 3 хвилини? | (Зелений) (3*60/(50+5+20)=2(30ост.)) | 4 |
|
|
|
| 28 балів |
Позакласний захід для 7-их класів “Математична казка на новий лад” з використанням мультимедійних технологій.
Мета: 1.Розвиток цікавості в учнів до вивчення математики;
2.Перевірка знань та вмінь;
3.Розвиток творчих здібностей учнів;
4.Виховання взаємодопомоги учнів один одному;
Умови: 1.Гра проводиться за допомогою мультимедійних засобів;
2.Клас ділиться на три команди по 6 учнів;
3.Вибір журі;
4.Пояснення умов,оцінювання конкурсів(оцінюється швидкість та правильність виконання завдання).
Обладнання: картки з завданням;
Перед початком гри потрібно представити журі, розповісти о критеріях оцінювання В процесі розповіді казки командам надаються завдання.
Після закінчення гри підводиться підсумок.
День 3й
Гра “Міс Математика.
Змагання юних математиків.
Другий тур шкільної олімпіади
Гра “Міс Математика”
Напередодні проведення змагання було відібрано 5 претендентів на це звання за допомогою математичного диктанту за курс алгебри та геометрії.
Змагання проводиться в класі. План змагання
тур. «Хто найшвидший». Вболівальники пропонують розв'язати задачу з підручника «Геометрія» претендентці (не своїй). Жодна претендентка не знає,
який номер та з якої теми вона буде розв'язувати задачу.
тур.«Хто найуміліший». Накреслити коло одночасно лівою та правою рукою.
3 тур.«Хто найпрактичний». Без лінійки відміряти 75 см стрічки.
4 тур.«Хто найоригінальніший». Придумати нову геометричну фігуру, дати їй назву та описати її властивості. Наприклад,

— спіраль Зазнайки

— синусоїда невпевненого
тур. «Хто найкрасивіший». Кожна з учасниць демонструє своє вбрання, яке вона сама пошила. Єдина умова: вбрання повинно бути пошито з геометричних фігур та підручних матеріалів.
тур. «Хто краще знає пісні». Учасниці по черзі співають два — три рядки пісень, в яких згадується математика - числа або фігури.
Підсумок гри.
Нагородження. Всіх учасниць гри нагороджено: за 1 місце — звання «Міс Математика», решта отримають звання «Міс Точність», «Міс Досконалість», «Міс Оригінальність»,«Міс розумність».
Змагання юних математиків
Організація змагання передбачає роботу «Крамниці», «Довідкового бюро», «Журі», «Лічильної комісії». У «крамниці» є задачі вартістю 2 бали, 3 бали, 4 бали. Кожен учасник гри може «купити» будь-яку задачу, сказавши «продавцеві»: «Прошу продати мені задачу за .... балів». Продавець дає покупцеві задачу і певну кількість зелених кружечків: 2, 3 або 4 в залежності від вартості задачі. Учень починає розв'язувати задачу і якщо зустрічається з труднощами, то звертається в «довідкове бюро».
У «довідковому бюро» працює кілька чоловік, кожен з яких обслуговує певний масив задач. Біля кожлого стоїть табличка, на якій указано номери задач, з яких можна одержати консультацію. Якщо підказка стосується умови задачі, то вона видається безплатно. Якщо підказка стосується розв'язання задачі, то за неї треба платити один зелений кружечок. У «довідкове бюро» можна звертатися кілька разів, але кожного разу треба «платити».
Якщо задача розв'язана, то правильність розв'язання оцінює журі. Учасник гри підходить до члена журі, біля якого теж стоїть табличка з номерами задач, які він перевіряє, показує свій розв'язок і дає необхідні пояснення. Якщо задача розв'язана правильно, то член журі обмінює зелені кружечки, що залишилися в учасника, на червоні.
Учасник гри може «купувати» кілька задач відразу або звертатись у «крамницю» кілька разів.
Коли інтерес згасає, а це буває хвилин через 40, то керівник змагань, як правило вчитель, пропонує здати червоні кружечки в «лічильну комісію». Члени «лічильної комісії» записують прізвище учасника гри та кількість червоних кружечків. Вони визначають переможця та призерів гри. Нагородою може бути оцінка з математики.
Під час роботи «лічильної комісії» діти грають у математичні ігри. Можна запропонувати такі ігри: стомахіон, гра в 15, шахи, шашки, комп'ютерні ігри.
Зразки задач для змагання
І. Задачі, що оцінюються 2 балами
Яке найбільше число точок перетину можуть мати п'ять різних прямих? Свої міркування проілюструйте за допомогою малюнка.
Знайдіть таке розміщення 10 точок, при якому вони визначають 10 прямих.
Відрізок АВ перетинають 5 прямих. На скільки частин вони ділять цей відрізок?
На прямій відмічені точки А, В, С, О, N так, що АВ=ВС=СВ=ВК. Які ще рівні відрізки визначають ці точки?
Знайдіть величину кута між хвилинною і годинною стрілкою о 14 год 30 хв?
Знайдіть величину кута між хвилинною і годинною стрілкою о 16 год 15 хв?
Знайдіть величину кута між хвилинною і годинною стрілкою о 19 год 20 хв?
Прямокутні трикутники мають по рівному катету, а гострі кути, що прилягають до цих катетів відповідно дорівнюють 42° і 48°. Чи рівні ці трикутники?
При перетині двох прямих утворились 4 кути, один з них на 18° більший від іншого. Знайдіть величину кожного кута
У трикутнику АВС ∟А=∟В. На сторонах АС і ВС відповідно від кладені рівні відрізки АК і ВМ. Чи рівні трикутники АВК і ВАМ?
Два кути трикутника рівні. Чи рівні бісектриси цих кутів?
Чи можна вважати два відрізки паралельними, якщо вони не мають жодної спільної точки?
Скільки гострих кутів може бути серед зовнішніх кутів трикутника?
Один із кутів рівнобедреного трикутника дорівнює 100°. Знайдіть решту кутів трикутника.
Половина числа дорівнює 15. Чому дорівнює його третина?
У вас є пиріг вагою 600гр.Розріжте пиріг на шматки так, щоб можна було його поділити поріїіііу між нашими друзями, якщо вам заздалегідь невідомо, скільки їх буде: троє чи четверо.
Володимир, Сашко, Ігор і Олекса ловили рибу. Усі разом зловили 40 йоржів. Володимир піймав на 4 рибини більше від Сашка, Сашко — на 4 рибини більше, ніж Ігор, Ігор — на 4 більше від Олекси. По скільки йоржів піймав кожний?
Число 20 збільшили на 10%, а потім одержане зменшили на 10%. Яке число одержали?
Як з трьох сірників, не ламаючи їх, зробити 4?
Хочуть розкласти ЗО яблук на 3 купки так, щоб число яблук у кожній купці було непарним. Чи можна це зробити?
II. Задачі, що оцінюються трьома балами
Написано цифри 1; 2; 3; 4; 5. Не змінюючи порядку цифр, поставте між ними знаки дій так, щоб утворилось число 100.
З ящика чаю, що вміщує 1100 г, треба відсипати 1 кг чаю. Як зробити це з допомогою терезів, якщо гир немає, але є пакети вагою в 300 г і 650 г?
На скільки збільшиться величина дробу, якщо до чисельника додати десяту частину знаменника?
Довести, що сума двох будь-яких послідовних непарних чисел ділиться на 4.
Довести, що число п3 - п при всіх натуральних п ділиться на 6.
Відрізок АВ перпендикулярний відрізку СВ і проходить через його середину. Чи рівні трикутники АВС і АВВ?
«Один чоловік вип'є діжку квасу за 14 днів, а з жоною вип'є ту діжку за 10 днів. Запитується, за скільки днів жона його одна вип'є тусаму діжку квасу».
Чи може сума трьох послідовних натуральних чисел бути простим числом?
Чотири теслярі хочуть побудувати будинок. Перший може побудувати будинок за рік, другий — за 2 роки, третій — за 3 роки, а четвертий — за 4 роки. Однак будували всі вчотирьох. За який час вони побудували будинок?
Один автомобіль долає відстань між містами за 10 годин, а другий долає цю ж відстань за 15 годин. Через скільки годин вони зустрінуться, якщо виїдуть з цих міст назустріч один одному?
Поділіть 7 пирогів між 12-ма чоловіками порівну, не розрізавши жодного пирога на 12 рівних частин.
III. Задачі, що оцінюються чотирма балами
Сторони двох кутів відповідно паралельні. Чи рівні ці кути?
АВ — бісектриса кута А трикутника АВС,DE ∕∕АС. Доведіть, що трикутник АЕ)Е рівнобедрений.
Сторони двох кутів взаємно перпендикулярні. Чи рівні ці кути?
За течією пароплав пропливає певну відстань за 3 год, а назад за 4 год. За який час пропливе цю відстань пліт?
Куб, поверхня якого пофарбована, розпиляли на 27 однакових за розміром кубиків. Скільки при цьому одержалось кубиків, пофарбованих з трьох сторін, з двох, з однієї, зовсім не пофарбованих?
Андрій пішов з батьком у тир. Домовленість була така: Андрій робить 5 пострілів і за кожне влучення в ціль одержує право зробити ще 2 постріли. Андрій зробив 17 пострілів. Скільки разів він влучив у ціль?
У таблицю вписано числа за деяким правилом. Знайдіть це правило і впишіть число, якого не вистачає.
8. Дідусь з трьома онуками вийшов погуляти в парк. Знайомий дідуся, що зустрівся з ними, спитав скільки років кожному з них. Іванко сказав: «Я молодший Петруся і мені більше 5 років». Петрусь промовив: «Я молодший Сашка на 3 роки». А Сашко сказав: «Нам всім разом втроє менше, ніж дідусеві, а разом з дідусем нам рівно 100 років». Скільки років кожному із онуків?
День 4й
Математичне кафе для учнів 8 класів
Без математики нині, як без рук (КВК між командами 10 класу).
Математичне кафе.
Матеріал для учнів 8-го класу.
Тема: Розв’язання логічних задач і задач на кмітливість. Лист Мебіуса.
Мета: - розвиток пізнавальної і творчої діяльності учнів;
- прививати навички самостійного пошуку нових закономірностей, пробудження допитливості;
- формування і розвиток інтересу учнів до занять математикою, розширення математичного кругозору учнів.
Форма заняття: дидактична гра.
І етап. Організаційний момент.
ІІ етап. Логічний тренінг.
Що більше, добуток чи сума цих чисел: 0,1,2,3,4,5,6,7,8,9?
2.
3.
ІІІ етап. Знайомство з «Меню».
Салати.
«Математичний єралаш» (рахуй, думай, відгадуй).
«Математичні обгонялки» (розв’язання задач на смекалку).
Перші блюда.
1. Юшка математична.
Другі блюда.
Лист Мебіуса (історична довідка).
Мебіус і топологія (експеримент).
Напитки.
Математичний коктейль (афоризми, крилаті вирази про математику).
Десерт.
Грамоти (нагородження активних учасників).
ІV. Рахуй, думай, відгадуй.
Розставте цифри так, щоб сума цифр була одна і та ж по горизонталі і по вертикалі.
Розставте числа 1, 2, 3, 4 так, щоб по горизонталі і по вертикалі не було однакових цифр.
Заповни пропуски.
Відповідь: 26, 14.
Знайдіть Х.
20 = 20 + 18 + 16 + 14 + …+ Х.
Відповідь: -18.
Продовж ряд.
а) 1, 3, 7, 15, …
б) 2, 5, 10, 17, …
Відповідь: 31, 26.
(Колективне обговорення, переможець столик, де учні дали більшу кількість правильних відповідей).
V етап. Математичні обгонялки.
Назвіть прислів’я з натуральними числами.
(Переможець той, хто назве останнім прислів’я).
Розв’язання задач «Математична вікторина».
назвіть слова, в яких є по сто приголосних (100н, 100г, 100к, 100л)
за скільки хвилин розпилять зайці семиметрову колоду, якщо за одну хвилину вони відпилюють 1 м. ( 6 хвилин).
(Нагороджується той, хто дасть більше вірних відповідей).
VІ етап. «Математична юшка».
з шести дев’яток складіть 100;
одне число в чотири рази більше іншого, сума цих чисел 20. Знайди ці числа;
три числа додали, потім перемножили і отримали суму, яка дорівнює добутку цих чисел. Які це числа?
Котра зараз година, якщо частина суток, що залишилась вдвічі більше той, що пройшла?
Поставте замість * цифри, щоб отримати вірну рівність: 3**:*3 = 3*. (390:13 = 30).
( Перемагає той, хто дав більшу кількість правильний відповідей ).
VІІ етап. Завдання.
Знайдіть значення 1 + 2 + 3 + …+ 100.
Розповісти історію розв’язання цієї задачі. ( Розповідь учня, який підготував, цю історію).
VІІІ етап. Лист Мебіуса.
Учень розповідає, про односторонню поверхню, яку вперше розглянув в 1858 році німецький математик Август Мебіус, учень «короля математики» К.Гаусса. таємничий і знаменитий лист Мебіуса має дивовижні властивості: він має один край, одну поверхню. Вивченням його властивостей займається наука топологія. Демонстрація листа.
ІХ етап. Дивовижні властивості листа Мебіуса.
Експеримент для всіх.
Я беру бума жну стрічку, розділену по ширині навпіл пунктирною лінією. Тепер я перекручу стрічку один раз і кінці стрічки склею. Таким чином, я отримав знаменитий лист Мебіуса. А тепер ріжу ножицями склеєну стрічку посередині, вдовж пунктирної лінії. Як ви гадаєте, що я отримаю? Звичайно, якщо б я не перекручувала стрічку перед тим, як я її склеїла, то все було б просто: з одного широкого кільця, я б отримала два. А що відбудеться зараз? Ви бачите, що я отримала не два кільця, а одне, двічі вужче, але вдвічі довше.
Практичне завдання для усіх.
Візьміть паперові стрічки, клей, ножиці. Приготуйте лист Мебіуса і проведіть експеримент, про який я вам розповів.
Отримане кільце, перекрутіть двічі, а потім розріжте це кільце ще по середині.
Висновок: отримали два зчеплених між собою кільця, кожне з яких двічі перекручене. Ось такі несподівані речі відбуваються з простою паперовою стрічкою, якщо з неї склеїти лист Мебіуса.
Х етап. Домашнє завдання. Афоризми, крилаті вислови.
ХІ етап. Підсумки. Нагороди.
Без математики нині, як без рук
КВК між командами 10 класу.
1-а ведуча. Добрий день, дорогі діти.
2-а ведуча. Добрий день, шановні уболівальники.
1-а ведуча. Ми дуже раді вітати вас на нашому конкурсі веселих і кмітливих.
Сьогодні ви будете свідками найцікавішої боротьби юних веселих і винахідливих математиків з команд 10 класу.
Запрошуємо їх на сцену.
(Команди виходять на сцену).
2-а ведуча. Математика - наука молодих. Інакше й бути не може. Заняття математикою - це така гімнастика розуму, для якої потрібна вся гнучкість і вся витривалість молодості.
1-а ведуча. І. Хто в дитинстві займається математикою, той розвиває увагу, тренує мозок, волю, виховує в собі наполегливість і завзятість у досягненні мети.
2-а ведуча. Діапазон практичного застосування математики величезний! Яку б науку ви не вивчали, для якого б ВУЗу ви не вступали, в якій би галузі ви не працювали, всюди обов'язково потрібні математичні знання.
1-а ведуча.
Ти визнана давно главою всіх наук.
Потрібна нам ти завжди, скрізь і всюди.
Без математики ми нині, як без рук:
З тобою з казки дійсність творять люди.
Освоївши тебе, рвемося у політ,
Створили ми розумні вже машини.
Штурмуємо космічний світ
І різних фактів узнаєм причини.
2-а ведуча.
З тобою ми невпинно ростемо,
З тобою підкоряємо природу.
Твої досягнення ми віддамо
На благо будівничого народу.
Тим, хто вчить математику.
Тим, хто любить математику,
Тим, хто знає математику,
Тим, хто ще не знає, що він любить математику,
Цей КВК присвячується...
1-а ведуча. Багато залежить і від вас, шановні вболівальники, від того, наскільки активними ви будете...
2-а ведуча. ...І наскільки успішно виступите в змаганнях уболівальників.
1-а ведуча. Але в нашому змаганні категорично забороняється підказувати.
2-а ведуча. Журі може нагородити вболівальників за хорошу підтримку своєї команди.
1-а ведуча. Але журі має право зняти бали з команди, якщо її члени (уболівальники) порушують порядок змагань.
2-а ведуча. У спортивних змаганнях, як правило, першими на арену виходять судді. А наш КВК - це «інтелектуальний спорт».
1-а ведуча. Ось ми і представляємо склад журі.
(Називають голову, членів журі).
2-а ведуча. Сьогодні грають команди:
1-а ведуча. Привітання команд (максимальна оцінка 5 балів).
«Піфагори»
1.
Противник сьогодні
Серйозний у нас,
О, друзі поважні,
Вітаємо вас!
2.
Уболівальникам вірним
Великий привіт!
Сміливо за нами
В незнаного світ!
3.
Ми хочемо дуже
Сподобатись вам!
І вірим, що ви
Допоможете нам!
4.
Повага вам, судді!
Привіт вам, журі!
Та тільки суворо
Ви нас не журіть,
5.
І смійтеся з того.
Що викличе сміх,
Сміятися голосно
Й суддям не гріх!
«Архітеди»
Добрий день, шановні противники, гості, журі та всі присутні в цьому залі.
Любе журі, відтоді, як ви опустили перпендикуляр на площину наших сердець, ми не можемо знайти радіус, щоб описати свої почуття.
Ніяка таблиця логарифмів не може перелічити поривів наших зацікавлених душ тому, що вони - як вольтові дуги.
Просимо й благаємо вас, не будьте такими гордими й самовпевненими і підкоріться закону всесвітнього тяжіння.
Тобто притуліться до наших думок під кутом альфа.
5. Уболівальники, друзі, подруги, ми чекаємо від вас аплодисментів і незрівнянної підтримки, щоб по тілу
противників пробіг індуктивний струм і їхні серця «порізало» на тисячі геометричних фігур. Наша надія - це ви.
І. Привітання команд (до 5-ти балів).
Привітання команди «Піфагори».
Привітання команди «Архімеди».
II. Розминка (за правильну відповідь - 1 бал).
1. Як називається перпендикуляр, опущений з вершини кута на сторону?
Кут більший 90° і менший 180° називається...?
Кут, у якого сторони є доповняль ними півпрямими, називається ...?
Промінь, який ділить кут навпіл називається ...?
Які числа називаються цілими?
6. Фігура, що складається з двох півпрямих, які виходять з однієї точки, називається ...
Розділ геометрії, в якому вивчаються фігури на площині.
Основна геометрична фігура.
Фігура, яка складається з усіх точок площини, рівновіддалених від даної точки.
Частина площини обмежена колом.
Відрізок, який з'єднує дві точки кола.
Відрізок, який з'єднує вершину трикутника із серединою протилежної сторони.
Сторона трикутника, яка лежить проти прямого кута.
Відстань від точки кола до її центра.
Три мухи літають в кімнаті. Коли вони будуть знаходитись в одній площині?
16. Назва графіка квадратичної функції.
Півсотні поділити на половину.
Які числа в минулому вважали абсурдними, фіктивними, числами від сатани?
III. Конкурс художників (по одному учневі від кожної команди, максимально - З бали).
Завдання: Одночасно лівою і правою рукою намалювати три кола і три трикутники.
IV. Конкурс «Хто краще рахує?» (по одному учаснику від команди, по одному балу за кожне завдання).
1.1 4444:44=(101);
5555:55=(101);
4,444:44=(0,101);
5,555:55=(0,101);
44,4444:44=(1,0101);
2.3 555,55:55=(10,101);
V. Конкурс «Відгадування загадок»
(для всієї команди, по три загадки, одна загадка - один бал).
1.
Летіла птиця по морові
Над хатами морозним днем,
Згубила літеру в дорозі
І стала цифрою з нулем.
Що це таке? (Сорока; 40)
2.
Кругла куля непроста,
Голуба, велика:
Без будинків там міста,
Без води там ріки,
Без людей і без землі,
І шляхи, і гори,
І моря, і взагалі -
Всі земні простори.
Що це таке? (Глобус)
3.
Ці числа є великі,
А е і малюки.
Проте з них кожне має
Лише два дільники. (Прості числа)
4. Яке місто складається з 101 імені? (Севастополь)
Сім братів роками рівні, а імена різні (Дні тижня)
У двох матерів по п'ять синів і всі на одне ім'я. (Пальці рук)
Один говорить, два дивляться, два слухають. (Голова)
VI. Конкурс капітанів (по одній хвилині, по два бали).
1. На столі стоїть шість склянок. Три з них порожні, а в три налито воду. Зробити так, щоб порожні і повні склянки чергувалися. Взяти в руки можна тільки одну склянку.
(Треба перелити воду з другої склянки в п'яту і поставити порожню склянку на місце)
Чому дорівнює добуток всіх цифр нашої десяткової системи числення? (0)
Як за допомогою трьох прямих утворити 12 кутів?
4. Обчислити усно:
1) 982 - 4; (982 - 22 = (98 - 2)(98 + 2) = 9600)
2) 912 - 81
(912 - 92 = (91 - 9)(91 + 9) = 8200)
5. Біля стін квадратного бастіону потрібно було розмістити 16 вартових.
Комендант розмістив їх так:

по 5 біля кожної стіни. Потім прийшов полковник і незадоволений таким розміщенням сказав, що потрібно розмістити по шість вартових біля кожної стіни. Услід за полковником генерал наказав розмістити по сім чоловік біля стіни. Як це потрібно зробити?


6. Як з трьох нулів зробити два?
000 два
7. Рибалка ловив рибу. На запитання «Скільки ти впіймав риби?», відповів: «Половину восьми, шість без голови, дев'ять без хвоста». Скільки риби
впіймав рибалка?
(Жодної, оскільки-8-6-9- 000)
8. Як за допомогою однієї лінійки на малювати кут, що дорівнює даному?
(Продовжити сторони кута доповняльними півпрямими, утвориться верти кальний кут, що дорівнює даному)
Додаткові завдання
1. Записати тисячу 8-ма вісімками, використовуючи тільки знак «+»
(888 + 88 + 8 + 8 + 8= 1000)
2. Записати всі цифри 4-ма «2»
22 - 22 = О,
22 : 22 = 1,
2:2 + 2:2 = 2,
2-2 - 2 : 2 = З,
2-2-2 + 2 = 4,
2-2 + 2 : 2 = 5,
2-2-2 - 2 = 6,
(2 + 2°)2 -2 = 7,
2-2 + 2-2 = 8,
10) 22 : 2 - 2 = 9.
3.Він не любив розв'язувати квадратні рівняння за допомогою дискримінанта. Назвіть його (Франсуа Вієт).
Плата за користування кредитом.
VII. Підведення підсумків. Нагородження переможців.
День 5й 1. Внесок українських вчених у розвиток математики.
Лінійка “Підведення підсумків тижня математики”.
Анкетування учнів.
1. Внесок українських вчених у розвиток математики
Мета: ознайомити учнів з іменами видатних українських учених; розвивати уміння виступати з повідомленнями працювати з додатковою літературою зміцнювати почуття гордості за свій народ.
Хід уроку
1.Слово вчителя.
Творчий характер науки, шлях до відкриттів найкраще прослідковується під час знайомства з життям і по видатних її представників. Вивчення творчості великих людей захоплює: воно звеличує душу і спонукає до діяльності.
“Предмет математики є настільки серйозним, що корисно не втрачати випадку зробити його дещо цікавим”. Ця глибока думка належить Б. Паскалю.
Вивчення життя і творчості видатних математиків є актуальним, оскільки удосконалює загальну культуру . мислення, дисциплінує її, виховує об'єктивність, інтелектуальну чесність і, таким чином, сприяє формуванню наукового світогляду.
Математика, що висвітлюється в історичному плані, засвоюється набагато краще, глибше і легше.
На сьогоднішньому уроці я хочу поговорити про українських вчених, яких раніше називали російськими математиками.
Навіть Михайла Остроградського раніше називали російським математиком, хоч він народився і похований на Полтавщині, був українським патріотом. А коли і розмовляв російською, то з дуже виразним українським акцентом. А математиком у Російській імперії він був найвідомішим — першим після Л. Ейлера.
Талантами багата Україна!
Хай навіть, відбиваючись від орд,
Долаючи неволю і руїни.
Все ж геніїв народжує народ.
Один із них - Михайло Острогорадський —
Великий тілом, розумом і духом.
Найперший вчений у краю козацькім.
Властитель теорем і аксіом.
Нью-Йорський академік і туринський,
Паризький, римський —
між усіх широт
Відомий математик український,
Славетний український патріот.
(Г.П. Бевз)
Добре відомий також у всьому світі український математик Георгій Феодосійович Вороний — творець геометричної теорії чисел та інших нових напрямів. Побудовані ним математичні об'єкти виявилися дуже зручними для моделювання важливих задач з багатьох галузей знань: кристалографії, фізики, астрономії, електротехніки, хімії, мікробіології тощо. Учені всього світу все частіше використовують поняття: алгоритм Вороного, многокутники Вороного, розбиття Вороного.
Однією з яскравих зірок України на терені математики є академік Михайло Кравчук, який народився на Волині в с. Човниці. Учений-математик став легендарною постаттю в історії нашої держави. Поет німого числа, лицар математики, творець музики чисел, титан математичної думки, гордість української математики — це неповний перелік епітетів, якими нагороджують науковці, письменники, журналісти видатного математика XX ст. Михайла Кравчука.
Михайла Кравчука нема.
Людину мудру і святу
Жорстокість дика і німа
Звалила в вічну мерзлоту.
Таких — один на сотню літ
І на мільйони душ - один,
Його ж ви за колючий дріт
До голих нар і баланди.
(Г.П. Бевз)
Сьогоднішній урок-семінар ми проведемо за таким планом (план записано на дошці заздалегідь).
План
Вступне слово вчителя.
Розповіді учнів:
а) Прокопович Феофан;
б)Остроградський Михайло Васильович;
в)Вороний Георгій Феодосійович;
г) Астряб Олександр Матвійович;
ґ) Кравчук Михайло Пилипович;
д)Шиманський Іван Євгенович;
е)Латишева Клавдія Яківна;
е) Штокало Йосип Захарович;
ж)Далецький Юрій Львович;
з)Самойленко Анатолій Михайлович.
II. Виступи учнів.
1-й учень. Прокопович Феофан (1681-1736 рр.)
Одним з найвизначніших викладачів Київської академії (Києво-Могилянська Академія) був Феофан Прокопович.
Феофан Прокопович народився у Києві в 1681 р. і був названий Єлеазаром. Батько його помер дуже рано, скоро померла й мати, сироту взяв під свою опіку його дядько Феофан Прокопович, який славився освіченістю і красномовством. У кінці своєї діяльності був обраний ректором колегії, але доживав життя в Києво-Печерській лаврі й помер, коли племіннику було 11 років. Того самого року Елеазар почав навчатися в колегії. Вчився дуже добре і влітку 1697 р. закінчив філософське відділення. Після цього деякий час він продовжував освіту в Польщі, пішки дістався до Риму і почав навчання в колегії Св. Афанасія, створеній спеціально для навчання слов'ян-католиків і уніатів. Йому довелося постригатися в ченці-василіани і одержати нове ім'я - Самуіл Церейський. Учився він дуже добре, і керівництво колегії домоглося для нього дозволу користуватися Ватиканською бібліотекою, де серед інших він міг ознайомитися з творами, які на той час для широкого вжитку не призначалися, наприклад, з книгою Миколая Коперника «Про обертання небесних сфер», з творами Галілея. Після закінчення колегії (є дані, що після захисту магістерської роботи він одержав докторський ступінь) він протягом трьох років побував у багатьох європейських країнах і в 1704 р. повернувся до Києва. Під час перехрещення в православ'я одержав (за власним бажанням) ім'я свого дядька - Феофан Прокопович, став викладачем Київської академії, в 1707 р. — її префектом (тобто проректором). Того самого року починає викладати курс філософії. Філософські твори Прокоповича в перекладі з латинської українською мовою видано у трьох томах у 1979-1981 рр. Перша в перекладі має заголовок «Арифметика і геометрія» - два перших і найбільш плодовитих печатки математичних наук. У списку українських математиків-меодистів, які залишили слід в історії науки, ім'я Феофана Прокоповича хронологічно посідає перше місце.
Цей матеріал у рукописі відсутній, але включається поняття про конічні перерізи, тобто криві другого порядку, а також про сплави. У традиційних курсах, написаних за «Началами» Евкліда, цих відомостей немає, але Прокопович вважає, що їх слід розглядати.
У 1711-1715 рр. Феофан Прокопович - ректор Київської академії, а в 1715 р. Петро І викликав його до Санкт-Петербурга для виконання важливих церковних і державних доручень. З 1718 р. Прокопович - єпископ псковський, з 1712 р. - віце-президент синоду, з 1724 р. - архієпископ новгородський. Він брав участь у створені Петербурзької академії наук, відомий як автор ряду історичних та літературних творів.
Помер Прокопович у 1736 р.
2-й учень. Остроградський Михайло Васильович (24.09.1801 - 01.01.1862)
М.В. Остроградський народився в с. Пашенній (тепер Пашенівка) на Полтавщині в сім'ї дрібного поміщика. З 1810 р. навчався в пансіонаті при Полтавській гімназії. Потім продовжував навчання в Полтавській гімназії, але незабаром залишив її, щоб стати військовим. Через нестачу потрібних коштів мрії Остроградського про військову службу не здійснилися. У 1817 р. він вступив на фізико-математичний факультет Харківського університету. Перший рік учився погано і навіть на деякий час залишив університет, та через рік повернувся і в 1820 р. закінчив навчання, блискуче склавши всі іспити. Проте через реакційних викладачів, які звинувачували Михайла Васильовича в антирелігійних настроях, він не одержав документа про закінчення університету. У травні 1822 р. М.В. Остроградський виїздить удосконалювати свою математичну освіту до Парижа, де тоді працювали Лаплас, Фур'є, Коші та інші видатні математики. Повернувшись у 1828 р. на Батьківщину, оселився у Петербурзі. Працював професором спочатку в офіцерських класах Московського кадетського корпусу, а потім — в інституті інженерів шляхів сполучення (з 1832 р.), у Головному інженерному училищі (з 1840 р.), у Головному артилерійському училищі (з 1841 р.). Під час поїздки у рідне село захворів і помер. Похований у родинному склепі Остроградських у селі Пашенівці.
Наукові інтереси і світогляд М.В. Остроградського сформувалися ще в Харківському університеті під впливом А.Ф. Павловського і особливо професора математики, редактора Т.Ф. Осиповського. Поїздка до Франції і особисті зв'язки з багатьма вченими також багато йому дали — за час перебування в Парижі Остроградський досяг значних успіхів. Його першу самостійну працю - «Теорія хвиль у посудині циліндричної форми», подано до Паризької АН, було схвалена і опубліковано Академією. Уже в цей час для його досліджень характерні були загальність і глибина. М.В. Остроградський отримує місце професора в колегіумі Генріха IV, на яке було багато претендентів. Слава про успіхи М.В. Остроградського дійшла і до вчених кіл Петербурга. Уже в грудні 1828 р. його обирають ад'юнктом Петербурзької АН, у серпні 1830 р. - екстраординарним академіком з відділу прикладної математики. М.В. Остроградський залишив велику наукову спадщину. Його дослідження стосуються найрізноманітніших галузей математики і механіки: диференціального та інтегрального числень, вищої алгебри, геометрії, теорії ймовірностей, теорії чисел, аналітичної механіки, математичної фізики, балістики тощо. У галузі математичного аналізу Остроградському належить ряд мемуарів з різних питань. У 1834 р. він повністю розв'язав задачу про знаходження екстремуму кратного інтеграла, а згодом - задачу про відокремлення алгебраїчної частини інтеграла від раціонального дробу. У 1838 р. надрукував свою «Замітку про лінійні, диференціальні рівняння», в якій розкрив деякі властивості інтегрування лінійних диференціальних рівнянь методом варіації довільних параметрів. Ця теорема в навчальній літературі називається тепер теоремою Ліувілля, хоч Ліувілль довів її на 7 років пізніше. Багато теорем і формул Остроградського увійшло до курсу аналізу, але його ім'я при них не завжди згадується.
У 1828 р. М.В. Остроградський подав до Академії наук працю, присвячену теорії теплоти, в якій довів відому формулу, що зв'язувала інтеграл по об'єму з інтегралом по поверхні (формула Остроградського-Гаусса). У цій праці поставлено також питання про дослідження збіжності тригонометричних рядів і висловлено, задовго до Рімана, так званий принцип локалізації, який тепер широко використовується в теорії збіжності тригонометричних рядів і, звичайно, пов'язується тільки з ім'ям Рімана.
Після того, як Фур'є склав диференціальне рівняння поширення теплоти в твердому тілі, треба було знайти способи визначення шуканої температури тіла за заданими початковими умовами. Цю задачу в загальному вигляді вперше розв'язав М.В. Остроградський. Довгий час було невідомо, чи можна застосувати метод розв'язання рівняння теплопровідності Фур'є до випадку, коли поверхня тіла є поверхнею многогранника, складнішого, ніж прямокутний паралелепіпед.
М.В. Остроградський був прекрасним педагогом і організатором. Йому належить чимало навчальних посібників: «Посібник початкової геометрії», «Курс небесної механіки», «Лекції алгебраїчного і трансцендентного аналізу», «Програма і конспект тригонометрії для військово-навчальних закладів» тощо. У результаті викладацької і організаційно-педагогічної діяльності в Остроградського виробилася струнка система поглядів на викладання взагалі і математики зокрема. Ці погляди він виклав у друкованих працях, численних доповідях, записках, настановах, що їх видавало управління військових навчальних закладів, а також сам втілював у життя у викладацькій роботі. Під впливом цих його ідей ще в середині минулого століття було видано ряд методичних посібників, які пропагували досконалі і прогресивні методи викладання.
2-й учень. Вороний Георгій Фео-досійович (28,04.1868 - 20.11.1908)
Г.Ф. Вороний належить до когорти найбільш відомих українських математиків минулого. Визнаний фахівцями як найяскравіший талант у галузі теорії чисел на межі ХІХ-ХХ століть. За своє коротке життя Г.Ф. Вороний встиг надрукувати лише шість великих мемуарів та шість невеликих заміток. Але всі його роботи багаті новими глибокими ідеями, в них подається розв'язання ряду складних і важливих проблем, над якими працювало не одне покоління кращих математиків світу. Більш того, роботи Г.Ф. Вороного значною мірою визначили подальший розвиток певних напрямів сучасної математичної науки, таких, як геометрія чисел та аналітична теорія чисел. Життєвий шлях ученого за зовнішніми ознаками був звичайний. Родом із села Журавка на Полтавщині (тепер це село Варвинського району Чернігівської області). Г.Ф. Вороний після закінчення Прилуцької гімназії (1885 р.) вступив до Петербурзького університету. Після закінчення університету в 1889 р. його залишили для підготовки до професорського звання. У 1894 р. захистив магістерську дисертацію «Про цілі алгебраїчні числа, що залежать від кореня незвідного рівняння 3-го степеня» і був призначений професором Варшавського університету. У 1897 р. захистив докторську дисертацію «Про одне узагальнення алгоритму неперервного дробу», в якій дав нові алгоритми для обчислення основних одиниць у загальному кубічному полі алгебраїчних чисел від'ємного і додатного дискримінантів, які й досі є найкращими. Ці праці заклали основи загальної теорії невизначених рівнянь 3-го степеня. Важливі відкриття зробив учений у геометрії чисел, геометрії многогранників. Він поділив з Мінковським пріоритет у створенні геометрії чисел. Одна з його праць - «Дослідження про примітивні паралелоедри» (1908-1909 рр.) - тісно пов'язана з геометричними дослідженнями знаменитого вченого-кристалографа Є.С. Федорова; вона стосується і теорії квадратичних форм, і геометрії. Праця Вороного «Про одну задачу з теорії асимптотичних функцій» (1903 р.) тимулювала розвиток сучасної теорії чисел. За визначні заслуги в математиці Г.Ф. Вороний був удостоєний премії ім. Буняковського.
З 1898 р. Г.Ф. Вороний працював також професором Варшавського політехнічного інституту. Там він був деканом математичного факультету. Під час революційних подій 1905-1907 рр. університет та політехнічний інститут у Варшаві було закрито. Групу професорів цих вузів (серед них Г.Ф. Вороного) направлено в Новочеркаськ у зв'язку зі створенням там Донського політехнічного інституту. У 1908 р. Г.Ф. Вороний повернувся до Варшави. Життя його трагічно обірвалося у розквіті творчих сил — у результаті невдалої операції на нирці. За заповітом, він був похований у рідному селі.
4-й учень. Астряб Олександр Матвійович (4.09.1879 - 18.11.1962)
О.М. Астряб — відомий математик-педагог. Народився 4 вересня 1879 р. у м. Лубнах (тепер Полтавської обл.) у сім'ї вчителя. У 1899 р. закінчив Лубенську гімназію і вступив на фізико-математичне відділення природничо-історичного факультету Київського університету, який закінчив у 1904 р. з дипломом І ступеня.
У 1904-1905 навчальному році працював викладачем математики й фізики у Глуховській гімназії. З 1905 року викладав математику й фізику в київських комерційних училищах, математику й методику математики на вищих педагогічних курсах. У 1907 р. він їздив до Франції для вивчення викладання математики у французьких школах. У цьому ж році його обрали дійсним членом Київського фізико-математичного товариства, яке приділяло велику увагу питанням викладання математики у школі.
У 1922-1925 рр. О.М. Астряб читав лекції з математики і фізики на робітничих факультетах Київського політехнічного і Київського сільськогосподарського інститутів, працював на робітничому факультеті при Київському інституті народного господарства і в трудовій школі. З 1925 р. — доцент, а згодом професор Київського інституту народної освіти. З 1930 р. - професор Київського інституту соціального виховання (який потім було перетворено на Київський педагогічний інститут, нині НПУ ім. М.П. Драгомано-ва), завідував кафедрою Київського фізико-хіміко-математичного інституту. У 1936 р. О.М. Астряб очолив відділ методики математики Українського науково-дослідного інституту педагогіки.
Після визволення Києва від фашистських загарбників учений продовжив роботу в Українському науково-дослідному інституті педагогіки і в Київському педагогічному інституті. З перших років діяльності Олександр Матвійович Астряб працював над створенням підручників і посібників для школи. У 1909 р. надруковано його першу книжку «Наглядная геометрия», яка витримала 12 видань.
У 20-х роках О.М. Астряб багато працював над створенням підручників для молодшого (І-ІУ) і старшого (У-УІІ) концентрів трудової семирічної школи. Його «Наочна геометрія. Перший ступінь» (1922 р.), «Задачник до наочної геометрії» (1923 р.) і «Курс опьітной геометрии. В четьірех частях» (1923 р.) було побудовано за індуктивно-лабораторним принципом. З 1947 р. працював завідуючим кафедрою математики Київського педагогічного інституту ім. О.М. Горько-го.
5-й учень. Кравчук Михайло Пилипович (27.03.1892 - 9.03.1942)
Михайло Пилипович Кравчук народився 27 березня 1892 р. в с. Човновиця Волинської області. Батько його працював землеміром. За характером своєї роботи він мав постійні зв'язки з народом, знав його важке життя і поділяв прагнення і надії.
Навчався Михайло у Луцькій гімназії, де виявив особливі здібності до математики та споріднених з нею дисциплін. Курс Луцької гімназії Михайло Кравчук закінчив із золотою медаллю. Він мріяв стати математиком. Але вступити до Київського університету йому відразу не вдалося. Адміністрація університету, стурбована політичною неблагонадійністю абітурієнта, повела з цього приводу офіційне листування з поліцейським управлінням. Нарешті, за наполягання прогресивної частини ради університету, Кравчука було прийнято на фізико-математичний факультет.
Михайло спочатку відвідував семінар Б.Я. Букреєва, члени якого проводили дослідження в галузі теорії функцій, математичного аналізу, вищої алгебри й варіаційного числення. Юнак із захопленням вивчав математику, був найактивнішим членом семінару. Згодом його перевели до семінару Д.О. Граве, де вивчали теорію груп, лінійну алгебру, теорію алгебраїчних чисел, матриць і квадратичних форм. Незабаром Кравчук зробив доповідь на тему «Змінні групи лінійних перетворень». Д.О. Граве у своєму виступі після доповіді зазначив, що Кравчук побудував усі змінні групи лінійних перетворень, які справджують квадратичні рівняння, що розробкою цих питань займався відомий німецький математик Шур і що Кравчук значно просунув уперед дослідження цієї проблеми. Конкретні результати цих досліджень матимуть застосування в математичній фізиці, механіці й геометрії.
Окрилений першим успіхом, Михайло Пилипович ще з більшою енергією і наполегливістю продовжує наукові пошуки. Коло його інтересів стає дедалі ширшим - тепер його цікавлять нові проблеми фізики, астрономії, філософії і навіть філології. Навесні 1914 р. він склав державні іспити за курс університету та одержав диплом першого ступеня. Науковий керівник Кравчука Д.О. Граве почав клопотатися, щоб його залишили при університеті на два роки для підготовки до професорського звання. Збори факультету ухвалили задовольнити прохання Д.О. Граве - порушити клопотання перед Міністерством народної освіти, щоб залишити М. Кравчука при університеті. Але тут знову на перешкоді стає його політична неблагонадійність. Студент Кравчук не припинив своєї опозиційної політичної діяльності, під час однієї демонстрації був заарештований. До того ж «малорос». Потрібно було дозвіл київського генерал-губернатора. Справа затяглася майже на півроку і лише в лютому 1915 р. дозволили залишити Кравчука при університеті для підготовки до професорського звання.
Із січня 1921 р. М.П. Кравчук почав читати курс лекцій з математики в Київському політехнічному інституті, а наступного року — в Київському інституті народної освіти (так тоді називали університет). У 1923 р. його запросили читати лекції до ветеринарного інституту.
Одночасно Михайло Пилипович продовжував розпочаті ним ще до революції дослідження з питань теорії квадратичних форм, матриць і визначників. Результатом цих досліджень стали чотири окремі праці, опубліковані у 1924 р. Одну з них - «Про квадратичні форми і лінійні перетворення» - він подав як докторську дисертацію, яку й захистив у 1924 р., діставши науковий ступінь доктора фізико-математичних наук.
Михайло Пилипович продовжує наполегливі пошуки й дослідження. За два роки (1926-1927 рр.) він написав близько сорока праць. Його ім'я стало відомим в академіях зарубіжних країн, а його праці друкуються у математичних виданнях Торонто, Цюріха, Палермо, Буенос-Айреса, у наукових журналах Паризької академії наук. Американська асоціація математиків запрошує Кравчука переїхати на постійну роботу до Америки, обіцяючи створити належні умови. Але Кравчук від цієї пропозиції відмовився, бо над усе ставив працю на благо своєї Батьківщини, свого народу. У 1925 р. Михайло Пилипович стає професором. На цей час він очолює кафедри вищої математики кількох столичних вузів, працює деканом Інституту народної освіти, а пізніше виконує обов'язки вченого секретаря Всеукраїнської академії наук. На всесвітньому конгресі математиків у Болоньї в 1928 р. було заслухано доповідь М.П. Кравчука «Про наближене інтегрування лінійних диференціальних рівнянь». Результати досліджень професора Кравчука можна було поширювати на системи диференціальних рівнянь.
29 червня 1929 р. Всеукраїнська академія наук обрала професора Михайла Пилиповича Кравчука своїм дійсним членом. На цей час він уже мав понад вісімнадцять опублікованих наукових праць. Усього Михайлові Пилиповичу належить понад 160 праць. Окремо слід виділити його працю з узагальненням так званих «поліномів Ерміта». Ці узагальнені поліноми, які запровадив Михайло Пилипович, відомі тепер як «поліноми Кравчука».
Його лекціями, що відзначалися багатством і глибиною змісту, чіткістю, особливою красою викладу, захоплювалося студентство, всі, хто його слухав.
Талантом і неабиякою ерудицією вченого захоплювався весь математичний світ.
І як блискавка - арешт. У розквіті сил 23 вересня 1938 р. М.П. Кравчука засуджено на 20 років тюремного ув'язнення та п'ять років заслання і відправлено на Колиму. Три зими і три літа каторжних робіт відбув він там, хворий, а 9 березня 1942 р. залишився вже на віки вічні в колимській мерзлоті.
Своєї реабілітації (1956) учений не дочекався.
6-й учень. Шиманський Іван Євгенович (20.01.1896 р.)
Іван Євгенович Шиманський народився в с. Кердани на Київщині. У 1915 р. вступив на фізико-математичний факультет Київського університету, а в 1916 р. був призваний в армію. Закінчив університет у 1922 р. У 1938-1941 рр. працював доцентом кафедри математики Київського педагогічного інституту. Під час Великої Вітчизняної війни деякий час перебував у лавах Червоної Армії, а потім працював у різних навчальних закладах. У 1944 р. повернувся до Київського педагогічного інституту. З 1953 р. завідував тут кафедрою елементарної математики і методики математики. У 1947 р. захистив дисертацію на ступінь
кандидата педагогічних наук. З 1964 р. - професор.
І.Є. Шиманському належить понад 40 науково-методичних праць. Найважливіші з них стосуються методики викладання математики у школі, зокрема введення поняття дійсного числа за методом суміжних наближень, що його розробив Є.Я. Ремез. У 1960 р. вийшов у світ підручник І.Є. Шиманського «Математичний аналіз», який широко використовується в педагогічних інститутах України.
7-й учень. Латишева Клавдія Яківна (14.03.1897 - 11.05.1956).
Клавдія Яківна Латишева народилася 14 березня 1897 р. в Києві. Середню освіту здобула у 2-й Київській жіночій гімназії. У 1916 році вступила на фізико-математичний відділ Київських жіночих вищих педагогічних курсів, які закінчила в 1921 р.
Клавдія Яківна Латишева - перша жінка в Україні, якій присудили ступінь доктора фізико-математичних наук.
Наукова діяльність К.Я. Латишевої почалася в 1920 р. під час навчання в аспірантурі Київського університету. Вона працювала над питанням застосування методів моментів до розв'язування диференціальних рівнянь. У 1936 р. Клавдія Яківна захистила кандидатську дисертацію на тему «Наближене розв'язування за допомогою способу моментів лінійних диференціальних рівнянь, що мають особливості в коефіцієнтах» і стала першою жінкою в Україні, що одержала ступінь кандидата фізико-математичних наук. Наступні її праці стосувалися диференціальних рівнянь з частинними похідними першого порядку, що не відповідають рівнянням характеристик даного диференціального рівняння.
Починаючи з 1946 р., К.Я. Латишева плідно працювала в галузі аналітичної теорії диференціальних рівнянь і в 1952 році захистила докторську дисертацію на тему «Нормальні розв'язки лінійних диференціальних рівнянь з поліноміальними коефіцієнтами», її науковий доробок складає 42 наукові праці, які присвячено аналітичній теорії диференціальних рівнянь, теорії моментів та теорії ймовірностей. Метод Фробеніуса-Латишевої застосовується для розв'язання систем диференціальних рівнянь з частинними похідними та задач електродинаміки, теорії коливань та ін. К.Я. Латишева любила математику, свою роботу і студентів, віддавала всю себе улюбленій справі. Померла Клавдія Яківна 11 травня 1956 р.
8-й учень. Штокало Йосип Захарович (15.11.1897 - 05.01.1987).
Йосип Захарович Штокало - доктор фізико-математичних наук (з 1964 р.), професор (з 1946 р.) академік АН України (з 1951 р.; член-кореспондент з 1948 р.), член-кореспондент Міжнародної академії історії науки (з 1966 р.). Народився в с.Скоморохи на Львівщині. У 1915-1931 рр. викладав математику в середній школі і технікумах. У 1931 р. закінчив Дніпропетровський університет і з того часу викладав математику у вищих навчальних закладах м. Харкова. У 1934 р. закінчив аспірантуру при Харківському науково-дослідному інституті математики і механіки. З 1941 р. працює в Інституті математики АН УРСР. У 1944-1951 і 1956-1970 рр. викладав у Київському університеті. У 1949-1956 рр. був головою Президії Львівського філіалу АН УРСР. З 1962 р. керував Сектором історії техніки і природознавства АН УРСР.
Наукові дослідження Й.З. Штокала, проведені в першій половині 30-х років, стосуються теорії конформних відображень, диференціальних рівнянь, варіаційної статистики і деяких питань теорії функцій комплексної змінної. У циклі праць, пов'язаних з його дисертацією («Асимптотичні і символіко-аналітичні методи в розв'язуванні деяких класів лінійних диференціальних рівнянь зі змінними коефіцієнтами»), вчений здобув ряд важливих результатів у загальній теорії лінійних диференціальних рівнянь: йому належить визначення критеріїв стійкості та нестійкості розв'язків лінійних диференціальних рівнянь з квазіперіодичними і майже періодичними коефіцієнтами. У 40-х роках Й.З. Штокало почав працювати над питаннями операційного числення. Він узагальнив деякі результати О. Хевісайда в галузі операційних методів, довів існування розв'язків, досліджуваних систем рівнянь за деяких припущень відносно їх коренів, здобув істотні результати в теорії символічного подання розв'язків диференціальних рівнянь. Ці дослідження він узагальнив у монографії «Операційні методи і їх розвиток у теорії лінійних диференціальних рівнянь із змінними коефіцієнтами» (1961 р.).
Помер Й.З. Штокало 5 січня 1987 р., у Києві.
9-й учень. Юрій Львович Далецький (1926-1997 рр.).
Без математики - не буде інженера.
(Ю.Л. Дилецький)
Юрій Львович Далецький - всесвітньо відомий математик, гордість вітчизняної науки. Про нього учні, колеги, друзі говорили, що він навіть на хвилину не уявляв своє життя без улюбленої науки, був математиком «від бога».
Народився Юрій Львович у Чернігові. З юних років захопився математикою, і любов до неї визначила все його життя. Лихоліття Другої світової війни відчув на власній долі — брав участь у бойових діях на 2-му Далекосхідному фронті, за мужність і відвагу відзначений урядовими нагородами.
Після демобілізації в 1946 р. вступив на механіко-математичний факультет Київського державного університету ім. Т.Г. Шевченка. Знання з математики при вступі були ґрунтовними, а ось атестата про середню освіту не було. Юнака вирішили взяти на навчання, він успішно опановував університетські математичні дисципліни і вже готувався до захисту диплома. Та на останньому курсі навчання деякі «доброзичливці» згадали про формальне порушення при вступі. Довелося з 5-го курсу університету йти на навчання... у випускний клас вечірньої школи, щоб отримати-таки документ про шкільну освіту. Ось так майбутньому академікові дошкуляли ті, хто не міг пробачити йому математичний талант, подарований природою та відшліфований працелюбністю і незламною вірою у власні сили.
З вересня 1951 р. вся подальша доля Ю.Л. Далецького протягом 46 років була тісно пов'язана з Київським політехнічним інститутом, в якому вчений пройшов тернистий шлях від асистента до академіка. У 1954 р. він захистив кандидатську дисертацію, у 1962 р. - докторську, академіком НАН України був обраний у 1992 р.
Науковою роботою Юрій Львович почав займатися ще в студентські роки під керівництвом С.Г. Крейна, який працював на той час у Києві. Значну роль у формуванні його наукових інтересів відіграло також співробітництво з корифеями сучасної науки М.Г. Крейном та І.М. Гельфандом.
Основні праці вченого присвячено дослідженню сучасних проблем математичного аналізу, теорії ймовірностей, теорії диференціальних рівнянь і математичної фізики. Ним написано біля 200 наукових праць, серед них значну частину складають ґрунтовні статті та монографії, які перекладено англійською мовою.
Важливий напрям досліджень Ю.Л. Далецького - еволюційні диференціальні рівняння в нескінченно-вимірних просторах. У цих дослідженнях відбилася широта наукових інтересів та ерудиція вченого. Ще з 1950 р. він почав застосовувати асимптотичні методи у теорії рівнянь з малим параметром у банахових просторах і досягнув у цьому напрямку значних результатів. Разом з М. Г. Крейном розвинув нескінченновимірний варіант теорії стійкості Ляпунова і експоненційну дихотомічну теорію. До скарбниці світової літератури з математики і теоретичної фізики увійшли важлива формула Далецького-Троттера про мультиплікативне представлення еволюційного інтеграла.
Вагомий внесок зробив учений у теорію міри, побудував теорію стохастичних диференціальних рівнянь у нескінченновимірних просторах, створив нову теорію — стохастичну диференціальну геометрію, що ґрунтується на взаємодії між стохастичними рівняннями і геометрією Рімана. До фундаментальних результатів Ю.Л. Далецького належить некомутативне узагальнення класичних формул Ньютона і Тейлора на функціональне операторне числення. При цьому отримані ним формули стали новими для скінченно-вимірного матричного випадку.
Серед учнів Ю.Л. Далецького є академіки, директори інститутів, декани факультетів, завідувачі кафедр, біля ЗО з них захистили кандидатські дисертації, 6 - докторські.
За вагомий внесок у розвиток національної освіти, успіхи у навчанні і вихованні молоді академіку Ю.Л. Далецькому присвоєно почесне звання - Заслужений діяч науки і техніки України.
10-й учень. Анатолій Михайлович Самойленко (народився в 1938 р.) .
«Навчання математики повинно формувати математичну культуру, розвивати Інтуїцію та збагачувати ерудицію студентів».
(А.М. Самійленко)
Академік ПАН України А.М. Самойленко народився 2 січня 1938 року в с. Потіївка, Радомишльського району Житомирської області. Закінчив механіко-математичний факультет Київського університету та аспірантуру Інституту математики. У 1963 році захистив, кандидатську дисертацію, а в 1967 році - докторську. З 1988 р. і посьогодні є директором Інституту математики НАН України. У 1978 р. був обраний членом-кореспондентом, а в 1995 р. - дійсним членом (академіком) Національної академії наук України. З 1998 р. - завідувач кафедри диференціальних рівнянь фізико-математичного факультету Національного технічного університету України
«Київський політехнічний інститут».
Перші наукові праці вченого з'явилися в 1961 р. За короткий час А.М. Самойленко став одним з провідних учених у теорії звичайних диференціальних рівнянь і теорії нелінійних коливань. Він є засновником наукової школи з теорії багаточастотних коливань та теорії імпульсних систем, що визнана математичними центрами світу. Учений опублікував близько 400 наукових праць, серед яких 16 монографій та 10 навчальних посібників. Більшість його праць перекладено іноземними мовами.
Наукові інтереси А.М. Самойленка охоплюють широке коло складних та актуальних математичних проблем. Міжнародне визнання його досліджень підтверджують загальновизнані в світовій математичній літературі терміни: «чисельно аналітичний метод Самойленка», «функція Гріна-Самойленка» та інші. Опубліковані ним монографії внесли фундаментальний вклад у розвиток математики та її застосувань.
Професор А.М. Самойленко викладає в Київському національному університеті імені Тараса Шевченка та Національному технічному університеті України «Київський політехнічний інститут». Він є президентом Українського та членом Американського математичних товариств, президентом Всеукраїнського благодійного фонду сприяння розвитку математичної науки, членом редакційних колегій українських та зарубіжних журналів.
А.М. Самойленко нагороджено орденом Дружби народів (1984 р.) та орденом «За заслуги» III ступеня (2003 р.), Почесною Грамотою Президії Верховної Ради України (1987 р,), е лауреатом Державних премій України в галузі науки і техніки (1985, 1996 рр.), Республіканської премії ім. М. Островського (1968 р.), премії Академії наук України ім. М. Крилова (1981р.) М. Боголюбова (1998 р.), премії НАН України ім. М. Лаврентьева (2000 р.), премії НАН України ім. М. Остроградського (2004 р.), «Соросівський професор» (1998 р.), заслужений діяч науки і техніки України (1998 р.), академік Європейської академії наук (2002 р.).
III. Підсумки уроку.
Учитель. Ви прослухали повідомлення наших доповідачів про вклад українських вчених у розвиток математики. Український народ дає людству не тільки першокласних спортсменів, митців, мислителів, а й математиків. І нам можна пишатися своєю Вітчизною, бо в неї були, є і будуть творці математичної науки, які піднімуть її на вищий щабель розвитку України.
• Відзначення активності учнів у на
писанні рефератів.
• Збір учнівських рефератів.
IV. Домашнє завдання.
Лінійка “Підведення підсумків тижня математики”
Анкетування учнів
Література
Майкл Фуллан. Сили змін. — Львів: Літопис, 2000. — 430 с.Образовательная система «Школа 2100»: Педагогика здравого смьісла. — М.: Баласс, 2003. — 368 с.
Образование в XXI веке: зкспериментьі й инновации. Сборник научно-практических материалов / Сост. й науч. Ред. А. С. Сиденко. — М.:АПКиПРО.-244с.
Поташник М. М., Ямбург Е. А. Й др. Управление качеством образования. — М.: Педагогическое общество России, 2000.
Фендрик Й. Г. Образовательное пространство субьекта й его проектирование. — М., 2003. — 154 с.
Баталіна А.Я. Цивилизационно – антропологический подход как методологический инструменталий в решении педагогических проблем /Педагогіка і психологія формування творчої особистості: проблеми і пошуки: Зб. Наук. Пр. /Редкол.: Т.І. Сущенко (відп. ред) та ін. –Київ – Запоріжжя. – Вип. 18. – 300с.
Добровольська Л.П. “Сучасні підходи та технології професійного відбору майбутніх учителів”. /Вісник Житомирського педагогічного університету/ Випуск 6, 2000р.
Добровольська Л. П. “Фаховий відбір абітурієнтів педагогічного вузу”. 13.00.04. Автореферат дисертації на здобуття наукового ступеня кандидата наук. К., 2001, 20 с.
Кучерявий О.Г. Інтегральна готовність до педагогічної діяльності як орієнтир професійного самовиховання майбутніх педагогів. /Педагогіка і психологія формування творчої особистості: проблеми і пошуки: Зб. Наук. Пр. /Редкол.: Т.І.Сущенко (відп. ред.) та ін. – Київ – Запоріжжя. – Вип.18.
Левківський М.Б. Відповідальність у контексті нової виховної парадигми. /Вісник Житимирського педагогічного університету / Випуск 6, 2000р.
Освітні технології: Навч. метод. посіб. /О.М. Пєхота, А.З. Кіктенко, О.М. Любарська та ін.; За заг. ред. О.М. Пєхоти. – К.: А.С.К., 2001. – 256с.
Педагогічна майстерність: підручник / І.А. Зязюн, Л.В. Крамущенко, І.Ф. Кривонос та ін.; За ред. І.А. Зязюна – К.:Вища шк., 1997. – 349с.
Словарь практического психолога /Сост. С.Ю. Головин. – Минск: Харвест, 1998. – 800с.
Современный словарь по педагогике /Сост. Рапацевич Е.С. – Мн.: «Современное слово», 2001. – 928с.
Фіцула М.М. Педагогіка навчальний посібник для студентів вищих педагогічних закладів освіти К.: „Академія” 2000. – 542с.
Ярошевский М.Г. История психологии. От античности до середины XX века: учебное пособие для высших учебных заведений. – 2-е изд. – М.:Издательский центр «Академия» 1997. – 416с.
Анджейчак А. Психолого-педагогічні умови формування творчої особистості дитини в освітньо-виховних закладах // Обдарована дитина. - 2000. - №5. - С.8-13.
24. Гурець Н.Т. Педагогічні умови розвитку творчої активності молодших школярів у гуртковій роботі: Автореф. дис. на здоб. наук. ступ. канд. пед. наук/ Харківський держ. пед.університет ім. Г.С.Сковороди – Харків, 1994. - 25 с.
25. Інтелектуальні ігри в початковій школі // Упоряд. Ю.Є. Бардакова. - Х.: Вид. група "Основа", 2005. - 192 с.
26. Ірклієнко В.С. Естетичне виховання молодших школярів засобами народних свят//Духовний розвиток особистості засобами мистецтва. Част. І-ІІ. - Чернігів – С.89-91
27. Карпенчук С.Г. Теорія і методика виховання. – К.: Вища школа, 1997.– 304 с.
28. Клюшина Н.В. Когда интересно и весело//Педагогічна Сумщина. – 1997.- №1. - С. 33-34
29. Кобзарь Б.С. Внеурочная воспитательная работа в школах и в группах продленного дня. – К.: Рад. школа, 1988. – 309 с.
30. Кремень В. Освіта в Україні: стан і перспективи розвитку /Неперевна професійна освіта. Теорія і практика. - К., 2001. - Вип.4
31. Крюкова Д. До проблем удосконалення навчально-виховного процесу в навчальному закладі // Рідна школа. – 2003.–№ 8.– С. 10-11.
32. Кутьев В.О. Внеурочная деятельность школьников. Пособие для классных руководителей. – М.: Просвещение, 1988. – 287 с
33. Леонтьев А.А. “Научите человека фантазии…”(творчество и развивающее образование)//Вопросы психологии. – 1998. - №5. –С.82-85
34. Литвиненко С.А. Українська народна казка як засіб розвитку творчості молодших школярів//Розвиток творчої особистості в системі безперервної освіти6: Зб. наук. пр. – Запоріжжя, 1995. – С. 79-83 .
35. Литвинова Н.І. Деякі аспекти підготовки учнівської молоді до творчої діяльності. Наук. метод. зб. Еколого0натуралістична творчість. - К., 2000. - Вип.1
36. Литвинова Н.І. Підготовка мвйбутніх педагогів для роботи з обдарованю молодд. //Теоретичні і методичні проблеми підготовки профшколи до впровадження інноваційних та інформаційних технологій навчання. - К., 2001
37. Локарева Г.В., Трунова Е.Ф. Воображение как элемент в развитии творческих способностей//Формування творчої особистості: проблеми і суперечності: Зб. наук. праць – Запоріжжя, 1995. – С. 93-99
38. Лук А.Н. Психология творчества. - М.: Наука, 1978. - 128 с.
39. Моляко В.А. Творческая одарённость и воспитание творческой личности. – К.: Знание, 1991
40. Моляко В.О. Психологическая система тренинга конструктивного мышления /Вопросы психологии. - 2000. - №5
41. Никитин Б.П. Ступеньки творчества или Развивающие игры. – М.,1990, 158 с., ил.
42. Паламарчук В.Ф. Як виростити інтелектуала?: Посіб. для вчителів. – К.: Знання, 1999. – 112 с.
43. Педагогические игры :Уч. пособие - Пермь :ПГПИ, 1991. – 104 с.
44. Пономарёв Я.А. Психология творчества и педагогика. - М.: Педагогика, 1976.
45. Приходченко К.І. Формування інтелекту учнів через розвиток їх творчих здібностей//Педагогічна скарбниця Донеччини. – 1998. - №2. – С.4-5
46. Развитие творческой активности школьников/Под ред. А.М.Матюшкина/Науч.-исслед. институт общей и педагогической психологии Акад. пед.наук. СССР. – М.: Педагогика, 1991. – 160 с.:ил.
47. Савенков А.И. Основные подходы к разработке концепции одарённости//Педагогика.– 1998. - №3.- С.24-29
48. Сафонова О.М. Навчає гра//Школа життєтворчості особистості:Науково-метод. збірник.- УСДОК,1995.- С. 144-148
49. Серапулова Є. Виховання обдарованої дитини // Початкова школа. - 2000. - №2. - С.3-5.
50. Селиванов В.С. Основы общей педагогики: Теория и методика воспитания. Учеб пособие для студ. высш. пед. учеб. зав. /Под. ред. В.А. Сластенина. – М.: «Академи». - 2000. 295 с.

 Получите свидетельство
Получите свидетельство Вход
Вход




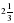 х =
х = 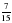














 Неделя математики в школе (0.18 MB)
Неделя математики в школе (0.18 MB)
 0
0 716
716 46
46 Нравится
0
Нравится
0


