
Линейная функция и её график
Выполнила учитель математики МКОУ Куминская СОШ Корзюк Н.Н.

Прежде чем решать задачу – прочитай условие
Жак Адамар
2

ТЕСТ
1. Что такое функция:
а) число;
б) зависимость у от х;
2. Какой вид имеет линейная функция:
в) зависимость х от у?
а) y = kx + m ;
б) у = kx² ;
3. Угловой коэффициент, это:
в) не знаю?
а) число m ;
4. Аргумент - это:
б) число k ;
в) переменная?
а) число m ;
б) зависимая переменная у;
5. Значение функции – это:
в) независимая переменная х?
а) зависимая переменная у;
б) число k ;
6. Что является графиком линейной функции?
в) независимая переменная х?
а) кривая;
б) окружность;
в) прямая?

ТЕСТ
1. Что такое функция:
а) число;
б) зависимость у от х;
2. Какой вид имеет линейная функция:
в) зависимость х от у?
а) y = kx + m ;
б) у = kx² ;
3. Угловой коэффициент, это:
в) не знаю?
а) число m ;
4. Аргумент - это:
б) число k ;
в) переменная?
а) число m ;
б) зависимая переменная у;
5. Значение функции – это:
в) независимая переменная х?
а) зависимая переменная у;
б) число k ;
6. Что является графиком линейной функции?
в) независимая переменная х?
а) кривая;
б) окружность;
в) прямая?

Определите по заданному правилу y = kx + m , где k , m – числа (коэффициенты) линейную функцию
у = – х + 16
у = 2х
у = 3х² – 4
у = (х – 5)²
у² = х + 4
у = ¼ х – 1

Графики каких функций являются линейными?
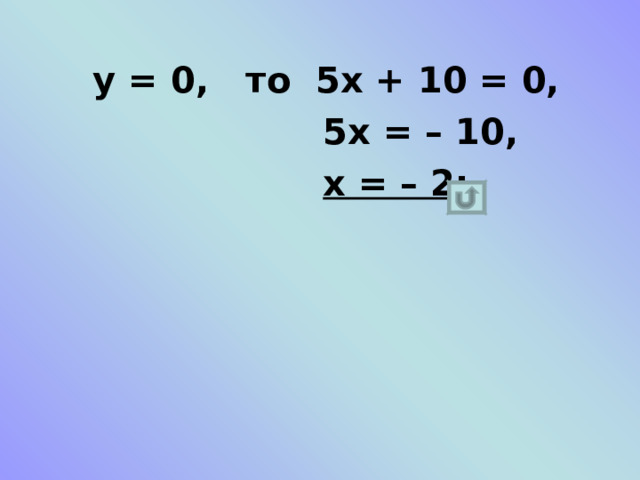
Найдите значение аргумента, при котором линейная функция у = 5х + 10 принимает значение 0 ; – 10 ; 9 .
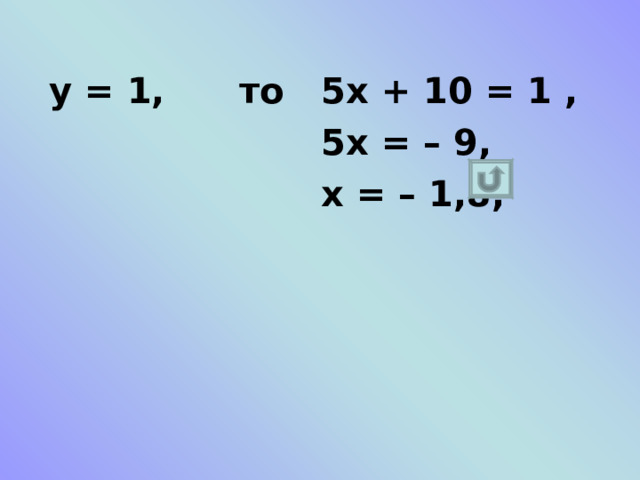
у = 0, то 5х + 10 = 0,
5х = – 10,
х = – 2 ;

у = 1, то 5х + 10 = 1 ,
5х = – 9,
х = – 1,8;

у = 9, то 5х + 10 = 9,
5х = – 1 ,
х = – 0,2.

Найдите значение линейной функции у = 0,5х – 4 , при данном значении аргумента 8 ; – 2 ; 0 .
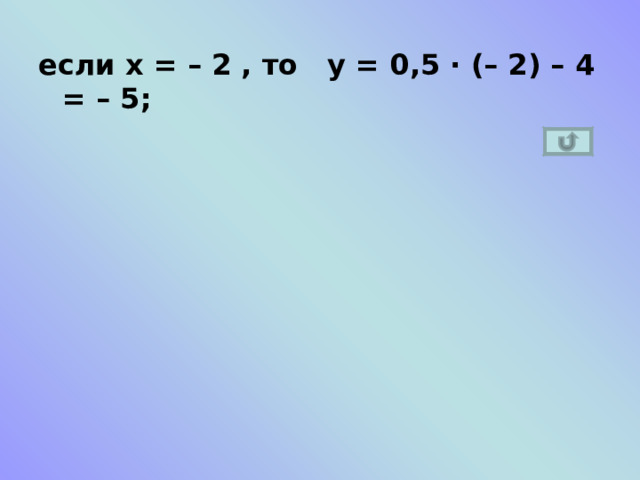
если х = 8, то у = 0,5 ∙ 8 – 4 = 4 – 4 = 0;
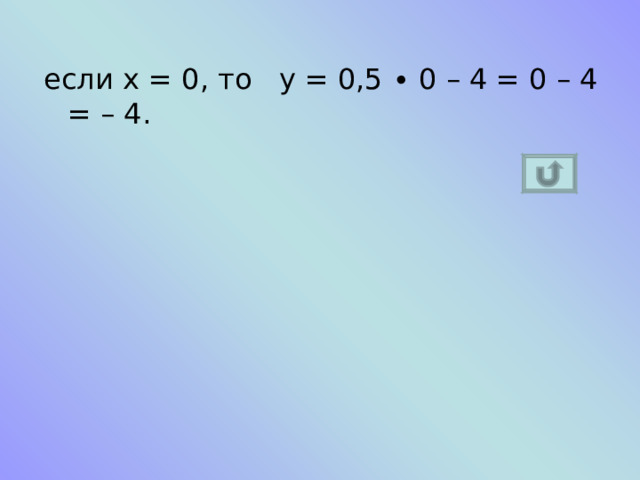
если х = – 2 , то у = 0,5 ∙ (– 2) – 4 = – 5;

если х = 0, то у = 0,5 ∙ 0 – 4 = 0 – 4 = – 4.

физминутка
Рисуй глазами треугольник,
теперь его переверни вершиной вниз.
И вновь глазами ты по периметру веди.
Рисуй восьмерку вертикально.
Ты головою не крути, а лишь глазами осторожно
Ты вдоль по линиям води, и на бочок ее клади.
Теперь следи горизонтально,
И в центре ты остановись.
Зажмурься крепко, не ленись.
Глаза открой ты, наконец.
Зарядка закончилась. Ты – молодец!
 0 k = 0 k 0 у – возрастает у параллелен оси х у - убывает 3. у = 0, х = . 4. у 0, х ϵ ; у 0, х ϵ . 5. у наиб . = (х = ); у наим. = (х = ). Е(у) = (– ∞; + ∞ ) Алгоритм Свойства функции. Запомни! " width="640"
0 k = 0 k 0 у – возрастает у параллелен оси х у - убывает 3. у = 0, х = . 4. у 0, х ϵ ; у 0, х ϵ . 5. у наиб . = (х = ); у наим. = (х = ). Е(у) = (– ∞; + ∞ ) Алгоритм Свойства функции. Запомни! " width="640"
Выводы:
Линейная функция у = kx + m
- Д(у) = (– ∞; + ∞ )
2. График – прямая, где k – угловой коэффициент
(монотонность)
k 0 k = 0 k 0
у – возрастает у параллелен оси х у - убывает
3. у = 0, х = .
4. у 0, х ϵ ; у 0, х ϵ .
5. у наиб . = (х = ); у наим. = (х = ).
- Е(у) = (– ∞; + ∞ )
Алгоритм
Свойства функции. Запомни!
![y Прочитайте свойства функции у = 2x – 2 по алгоритму, найдите наибольшее и наименьшее значения функции на [1;4] . -1 0 1 2 4 x -2](https://fsd.videouroki.net/html/2022/12/13/v_6397d766a24b2/img16.jpg)
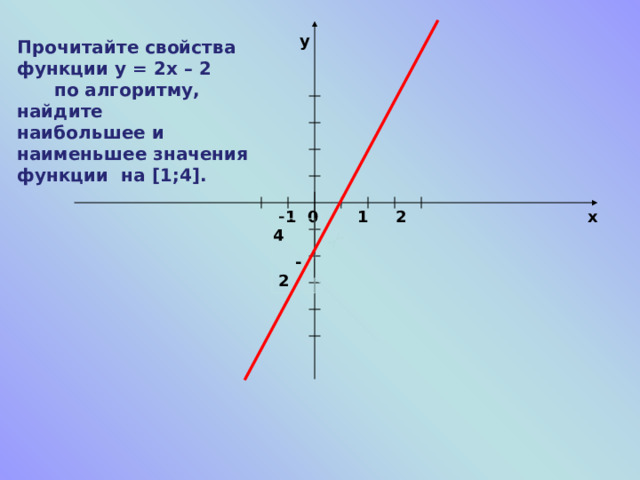
y
Прочитайте свойства функции у = 2x – 2 по алгоритму, найдите
наибольшее и наименьшее значения функции на [1;4] .
-1 0 1 2 4
x
-2

Самостоятельная работа
I вариант
II вариант
1.Постройте график функции
у = 5х - 1
у = – 2х + 5
2. Принадлежит ли графику функции точка
К (24; 121)?
3. Являются ли линейными функции, заданные формулами:
С (– 67; 129)?
а) у = 3х – 2;
а) у = (1 + х)²;
б) у = – ⅜ х + 9,7;
б) у = – 20,1х + 9;
в) у = 1 – х²;
в) у = 7х;
г) у = – 3.
г) у = – ⅝ + 0,2х.
Желаю успеха!

Декарт Рене (1596 – 1650 гг.)
Декарт Рене — французский философ, математик, физик и физиолог. Заложил основы аналитической геометрии, в которой с помощью метода координат все геометрические задачи переводил на язык алгебры. Ввёл обозначения для переменных, коэффициентов, степеней.

Ферма Пьер (1601-1665 гг.)
французский математик и физик. Заложил основы многих областей математики - аналитической геометрии, исчисления бесконечно малых, теории вероятностей. Ввел бесконечно малую величину в аналитическую геометрию. С именем Ферма связаны две замечательные теоремы - большая (иногда ее называют последней) и малая. Ферма исследовал общие виды уравнений 1-й и 2-й степени преобразованием координат. Ферма фактически осуществил операцию, называемую теперь дифференцированием, и применил ее для нахождения не только максимумов и минимумов, но и касательных к кривым.
26

Домашнее задание §8, читать теорию, рассмотреть примеры 3 - 5
на « 4 » - № 8.28. (а – г), 8.58. (г), 8.59. (г);
на « 5 » - № 8.50.
Дополнительно № 8.63* (по желанию)

- Развитие и образование ни одному человеку не могут быть даны или сообщены.
- Всякий, кто желает к ним приобщиться, должен достигнуть этого собственной деятельностью, собственными силами, собственным напряжением.
- Извне он может получить только возбуждение.
А.Дистервег


- ИИП «КМ-Школа», блог «БиблиоNETик@»
- http://wiki.km-school.ru/wiki/index.php

 Получите свидетельство
Получите свидетельство Вход
Вход












 Мультимедийная разработка урока по алгебре 7 класс "Линейная функция и её график" (1.23 MB)
Мультимедийная разработка урока по алгебре 7 класс "Линейная функция и её график" (1.23 MB)
 0
0 511
511 11
11 Нравится
0
Нравится
0



