Методические рекомендации
к практическому занятию по учебной дисциплине
«Математика: алгебра и начала математического анализа, геометрия»
для студентов 1 курса
на тему: «Решение рациональных уравнений и неравенств»
Цели: научить учащихся применять полученные знания, решать рациональные уравнения и неравенства.
Опорный теоретический материал:
Целые рациональные уравнения.
- первой степени: y=ax+b
- второй степени: ax2 + bx + c = 0
- выше второй степени: ах³+вх²+сх+d=0
Для решения уравнений выше второй степени применяют:
а) метод введения новой переменной
б) метод разложения на множители (группировка)
Рассмотрим примеры:
Пример 1.
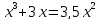
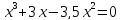
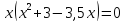
х=0 или 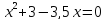
D=1
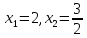
Ответ: 0,2,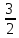
Пример 2.
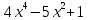 =0
=0
х²=у
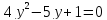
D=9
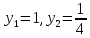
х²=1 х²=1/4
х=±1 х=±1/2
Ответ: х=±1 х=±1/2.
В более сложных случаях подстановка видна лишь после нескольких преобразований.
Пример 3.
(x2 + 2x)2 – (x +1)2 = 55.
(x2 + 2x)2 – (x2 + 2x + 1) = 55
x2 + 2x=t.
t2 – t – 56 = 0, t1 = – 7, t2 = 8.
Осталось решить x2 + 2x = – 7 и x2 + 2x = 8.
Дробно- рациональные уравнения.
Определение. Уравнения вида Р(х)/Q(х)=0, где Р(х) и Q(х) – многочлены, называются дробными.
Пример 4.
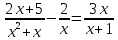

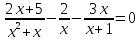
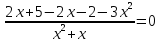
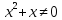
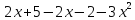
х≠0 -3х²+3=0
х≠-1 х=±1
Ответ: 1
НЕРАВЕНСТВА
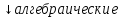
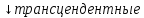
-целые
-дробно-рациональные
-иррациональные
Целые неравенства:
- неравенства первой степени (обычные линейные неравенства)
- неравенства алгебраической целой второй степени
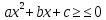
Пример 5.
Решается графически (с помощью параболы)
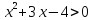
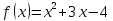
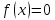
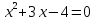
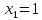
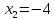
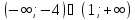
- выше второй степени: решаются а) методом замены
б) разложением на множители
Пример 6.
Ответ:
б)
x=2 x=- x=-5
Ответ: ()
Дробно- рациональные неравенства решаются методом интервалов по следующему алгоритму:
Разложить на множители и числитель и знаменатель
Нанести на числовую ось и проверить знаки на каждом интервале
Пример:
x=2 x=3 x=-1
Ответ: (-1;2)(2;3)
Тренировочные упражнения:
Решить неравенства:
Решить уравнения:
-1)(
(x-2)(x-1)(x+2)(x+3)=60
(x+2)(x+3)(x+8)(x+12)=
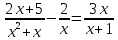
Пояснения к выполнению работы.
Задания представлены в таблицах по 6 вариантов.
На оценку «3» - удовлетворительно (таблица 1,) нужно решить два уравнения и два неравенства с одной переменной.
На оценку «4» - хорошо (таблица 2), нужно решить по одному уравнению и неравенству.
На оценку «5» - отлично (таблица 3), нужно решить по одному дробно – рациональному уравнению и неравенству.
На оценку «3» - удовлетворительно
Таблица 1
| Вариант 1 | 7(-3+2х)=-6х-1 | (х-4)(х-6)0 |
| | 4х²+3х+14≥9х² | |
| Вариант 2 | 2(7+9х)=-6х+2 | |
| | 2х²-12х-59 | |
| Вариант 3 | 6(5-3х)=-8х-7 | (х-4)(х+2)≥0 |
| | 9х²-3х+3 | |
| Вариант 4 | 6(9+4х)=4х-4 | х²-х |
| | 9х²+12х-84х²+36х-24 | |
| Вариант 5 | 4(2-3х)=-7х+10 | х²-х6 |
| | 10х²+2х+344х²-х+79 | |
| Вариант 6 | -4(5-4х)=х+1 | х²+11х≥-30 |
| | 9х²-16х-35≤4х²+х+5 |
На оценку «4» - хорошо
Таблица 2
| Вариант 1 | | 2х²+3х+37 |
| Вариант 2 | | 3х²+4х+1 |
| Вариант 3 | | 3х²+3х-6 |
| Вариант 4 | | 3х²-5х-32 |
| Вариант 5 | | 2х²+7х-13 |
| Вариант 6 | | 2х²+14х-20(х-6)² |
На оценку «5» - отлично
Таблица 3
| Вариант 1 | ||
| Вариант 2 | | |
| Вариант 3 | | |
| Вариант 4 | | |
| Вариант 5 | | |
| Вариант 6 | |
Список литературы
Ф.Ф. Лысенко, С.Ю. Клабухова. Математика. Подготовка к ГИА-2014.-Ростов-на-Дону:Легион, 2013. -304с. – (ГИА-9)
С.А. Шестаков, И.Р. Высоцкий, Л.И. Завич. Сборник задач для подготовки и проведения письменного экзамена по алгебре за курс основной школы: 9 класс.-М.:АСТ: Астрель, 2007. – 255,[1]с.
Ященко И.В.ОГЭ: 3000 задач с ответами по математике. Все задания части 1. М.: Издательство «Экзамен», издательство МЦНМО, 2016. – 463, [1]с

 Получите свидетельство
Получите свидетельство Вход
Вход












 Методические рекомендации к практическому занятию по учебной дисциплине «Математика: алгебра и начала математического анализа, геометрия» для студентов 1 курса на тему: «Решение рациональных уравнений и неравенств» (28.74 KB)
Методические рекомендации к практическому занятию по учебной дисциплине «Математика: алгебра и начала математического анализа, геометрия» для студентов 1 курса на тему: «Решение рациональных уравнений и неравенств» (28.74 KB)
 0
0 817
817 58
58 Нравится
0
Нравится
0


