ИССЛЕДОВАТЕЛЬСКАЯ РАБОТА
Петуровой Елизаветы Андреевны
ТЕМА
«Приемы устного счета»
Содержание
| ВВЕДЕНИЕ | 3 |
| Глава 1. Теоретическая часть | 5 |
| 1.1 Историческая справка | 5 |
| 1.2 Приемы устного счета | 8 |
| 1.3 Признаки делимости | 9 |
| 1.4 Алгоритмы ускоренных вычислений | 9 |
| 1.5 Задачи |
|
| Глава 2. Практическая часть | 13 |
| ЗАКЛЮЧЕНИЕ | 16 |
| СПИСОК ЛИТЕРАТУРЫ | 17 |
Введение
Устный счет - математические вычисления, осуществляемые человеком без помощи дополнительных устройств (компьютер, калькулятор и тд) и приспособлений (ручка, карандаш, бумага и тд).
Процесс устного счета можно рассматривать как технологию счета, объединяющую представления и навыки человека о числах, математические алгоритмы арифметики.
Актуальность работы заключается в том, что, зная различные приемы устного счета, можно существенно сократить время на решение примеров и задач, не допустить ошибок, поэтому я считаю нужным систематизировать данные и провести опытную часть работы.
Объект исследования: приемы устного счета
Предмет исследования: эффективность приемов устного счета
Цели: выявить эффективность приемов устного счета
Для достижения целей поставлены следующие задачи:
1) Описание различных приемов устного счета
2) Проведение опроса
3) Анализ полученных данных
Методы: теоретический анализ специальной литературы, опрос.
Теоретическая значимость предстоящей работы состоит в том, что будут систематизированы знания о приемах устного счета. Данная работа может помочь школьникам для подготовки к экзаменам.
Практическая значимость предстоящей работы определяется
1) Проведения опроса с целью выявить эффективность приемов устного счета
2) Описанием полученных результатов
Я выбрала именно эту тему исследовательской работы, так как приемы устного счета могут помочь ученикам на экзаменах и в жизни.
Глава 1. Теоретическая часть
1.1 Историческая справка
Феномен особых способностей в устном счёте встречается с давних пор. Ими обладали многие учёные, в частности, Андре Ампер и Карл Гаусс. Однако, умение быстро считать было присуще и многим людям, чья профессия была далека от математики и науки в целом.
До второй половины XX века на эстраде были популярны выступления специалистов в устном счёте. Иногда они устраивали показательные соревнования между собой, проводившиеся в том числе и в стенах уважаемых учебных заведений, включая, например, Московский государственный университет имени М. В. Ломоносова.
Среди известных российских «супер счётчиков»:
Арон Чиквашвили — «чудо-счётчик»
Роман Арраго
Алексис Лемэр
Шакунтала Дэви
Вильям Клайн
Луис Флери
Юзеф Приходько
Давид Гольдштейн
Игорь Шелушков
Горный (Яшков) Юрий Гаврилович
А. В. Некрасов — «человек-компьютер»
Владимир Кутюков — «человек-календарь»
Среди зарубежных:
Борислав Гаджански
Вильям Клайн
Жак Иноди (итал.)русск.
Луи Флери
Мадемуазель Осака
Морис Дагбер
Томас Фулер
Урания Диамонди
Шакунтала Дэви
Юсниер Виера — кубино-американский математик, феноменальный счётчик, мировой рекордсмен в области устного календарного исчисления.
Хотя некоторые специалисты уверяли, что дело во врождённых способностях, другие аргументированно доказывали обратное: «дело не только и не столько в каких-то исключительных, „феноменальных“ способностях, а в знании некоторых математических законов, позволяющих быстро производить вычисления» и охотно раскрывали эти законы.
Истина, как обычно, оказалась на некоей «золотой середине» сочетания природных способностей и грамотного, трудолюбивого их пробуждения, взращивания и использования. Те, кто уповают исключительно на волю и напористость, со всеми уже хорошо известными способами и приёмами устного счёта обычно при всех стараниях не поднимаются выше очень и очень средних достижений. Более того, настойчивые попытки «нагрузить» мозг такими занятиями, как устный счёт, шахматы вслепую и т. п. легко могут привести к перенапряжению и заметному падению умственной работоспособности, памяти и самочувствия (а в наиболее тяжёлых случаях — и к шизофрении). С другой стороны, и одарённые люди при беспорядочном использовании своих талантов в такой области, как устный счёт, быстро «перегорают» и перестают быть в состоянии длительно и устойчиво показывать яркие достижения.
В настоящее время в прибалтийских странах и Белоруссии набирает популярность соревнование по устному счёту среди школьников под названием Пранглимине (эст. Pranglimine), проводящееся в Миксике (Эстония).
Начиная с 2004 года, один раз в два года проводится Мировой чемпионат по вычислениям в уме, на который собираются лучшие из ныне живущих феноменальных счётчиков планеты. Соревнования проводятся по решению таких задач, как сложение десяти 10-значных чисел, умножение двух 8-значных чисел, расчёт заданной даты по календарю с 1600 по 2100 годы, корень квадратный из 6-значного числа. Также определяется победитель в категории «Лучший универсальный феноменальный счётчик» по итогам решения шести неизвестных «задач с сюрпризом».
1.2 Приемы устного счета
1) Сложение
Основное правило для выполнения сложения в уме звучит так:
Чтобы прибавить к числу 9, прибавьте к нему 10 и отнимите 1; чтобы прибавить 8, прибавьте 10 и отнимите 2; чтобы прибавить 7, прибавьте 10 и отнимите 3 и т.д. Например:
56+8=56+10-2=64
65+9=65+10-1=74
2) Сложение двухзначных чисел
Если цифра единиц в прибавляемом числе больше 5, то число необходимо округлить в сторону увеличения, а затем вычесть ошибку округления из полученной суммы. Если же цифра единиц меньше, то прибавляем сначала десятки, а потом единицы. Например:
34+48=34+50-2=82
27+31=27+30+1=58
3) Сложение трехзначных чисел
Складываем слева на право, то есть сначала сотни, потом десятки, а затем единицы. Например:
359+523= 300+500+50+20+9+3=882;
456+298=400+200+50+90+6+8=754.
4) Вычитание
Чтобы вычесть два числа в уме, нужно округлить вычитаемое, а затем подкорректировать полученный ответ.
56-9=56-10+1=47;
436-87=436-100+13=349.
5) Вычитание числа меньше 100 из числа больше 100
Если вычитаемое меньше 100, а уменьшаемое больше 100, есть простой способ вычислить разность в уме.
134-76=58
76 на 24 меньше 100. 134 на 34 больше 100. Прибавим 24 к 34 и получим ответ: 58.
152-88=64
88 на 12 меньше 100, а 152 больше 100 на 52, значит
152-88=12+52=64
6) Умножение на 4
Чтобы устно умножить число a на 4, его дважды удваивают.
Обоснование: а·4=а·2·2.
Например:
122·4=244·2=488
335·4=670·2=1340
7) Умножение на 5
Чтобы устно умножить число на 5, его умножают на 10 и делят на 2, то есть приписывают к числу 0 и делят пополам.
Обоснование: а·5=а·10:2.
Например:
74·5=74·10=740:2=370
243·5=243·10=2430:2=1215
При умножении числа на 5 четного числа 2а, проще сначала делить число пополам, а затем умножить результат на 10.
Обоснование: 2а·5=2а:2·10=а·10.
Например:
74:2·10=37·10=370
8) Умножение на 6
Чтобы умножить число на 6 его умножают на 5 и прибавляют множимое. Чтобы умножить число на 5 его умножают на 10 и делят на 2.
Обоснование: а·6=а·(5+1)=а·10:2+а.
Например:
36·6=36·5+36=36:2·10+36=180+36=216
164·6=164·5+164=164:2·10+164=820+164=984
9) Умножение на 8
Чтобы умножить число на 8, его трижды удваивают.
Обоснование: а·8=а·2·2·2=2а·2·2=4а·2
Например:
37·8=74·4=148·2=296
217·8=434·4=868·2=1736
10) Умножение на 9
Чтобы умножить число на 9, умножают его на 10 и отнимают множимое.
Обоснование: а·9=а·(10-1)=10а-а.
Например:
89·9=89·10-89=801
375·9=375·10-375=3375
11) Умножение на 11
1 способ - Чтобы устно умножить число на 11, его умножают на 10 и прибавляют множимое.
Обоснование: а·11=а·(10+1)=10а+а.
Например:
87·11=87·10+87=870+87=956
645·11=6450+645=7095
2 способ-Чтобы любое двузначное число умножить на 11, нужно сложить его первую и последнюю цифру и цифру-результат вписать в середину двухзначного числа. Если суммы –двузначное число, то необходимо прибавить к первому числу единицу.
Например:
54*11=5(5+4)4=594
58*11=5(5+8)8=638
12) Умножение на 15
Чтобы устно умножить число на 15, его умножают на 1,5 (пункт 21) и умножают на 10.
Обоснование: а·15=а·1,5·10=1,5а·10.
Например:
18·15=18·1,5·10=270
45·15=45·1,5·10=675
13) Умножение на 50
Чтобы устно умножить число на 50, его умножают на 100 и делят на 2.
Обоснование: а·50=а·100:2=100а:2.
При умножении числа на 50 четного числа 2а, проще сначала делить число пополам, а затем умножить результат на 100.
Например:
46·50=46:2·100=23·100=2300
847·50=847·100=84700:2=42350
14) Умножение на 99
Чтобы устно умножить число на 99, его умножают на 100 и отнимают множимое.
Обоснование: а·99=а·(100-1)=100а-а.
Например:
46·99=46·100=4600-46=4554
745·99=745·100=74500-745=73755
15) Умножение чисел на 22, 33,… ,99
Чтобы двузначное число умножить на 22, 33, 44, …, 99, надо этот множитель представить в виде произведения однозначного числа (от 2 до 9) на 11, то есть 33 = 3 х 11; 44 = 4 х 11 и т.д. Затем произведение первых чисел умножить на 11(пункт 12).
Примеры:
18 х 44 = 18 х 4 х 11 = 72 х 11 = 792
42 х 22 = 42 х 2 х 11 = 84 х 11 = 924
13 х 55 = 13 х 5 х 11 = 65 х 11 = 715
Кроме того, можно применить закон об одновременном увеличении в равное число раз одного сомножителя и уменьшении другого:
28 х 33 = (28 х 3) х (33:3) = 84 х 11 = 924
48 х 22 = (48 х 2) х (22:2) = 96 х 11 = 1056
16) Умножение на 9, 99, 999
К первому множителю приписать столько нулей, сколько девяток во втором
множителе, и из результата вычесть первый множитель.
286∙9=286∙(10 - 1)=2860 – 286=2574,
23∙99=23∙(100 - 1)=2300 – 23=2277,
18∙999=18∙(1000 - 1)=18000 – 18=17982
17) Умножение чисел на 111 ,1111, 11111 и т. д.
Зная, как умножать на 11(пункт 12), можно легко умножать на 111. Рассмотрим примеры. Если сумма цифр меньше 10, то легко умножать на 111, 1111 и т.д.
Примеры:
32 х 111 = 3 (3+2) (3+2) 2 = 3552
45 х 111 = 4 (4+5) (4+5) 5 = 4995
26 х 1111 = 2 (2+6) (2+6) (2+6) 6 = 28 886
52 х 1111 = 5 (5+2) (5+2) (5+2) 2 = 57 772
Чтобы двузначное число умножить на 111, 1111 и т.д., надо мысленно цифры этого числа разомкнуть на два, три и т.д. шага, сложить цифры и записать соответствующее количество раз их сумму между числами.
42 х 111 111 = 4 (4+2) (4+2) (4+2) (4+2) (4+2) 2 = 4666662
Разомкнуть 4 и 2 на 5 шагов. Если единиц 6, то шагов будет на 1 меньше, то есть 5. Если единиц 7, то шагов будет 6 и т.д.
Немного сложнее, если сумма цифр равна 10 или более 10.
Примеры:
57 х 111 = 5 (5+7) (5+7) 7 = 5 (12) (12) 7 = (5+1) (2+1) 27 = 6327;
86 х 111 = 8 (8+6) (8+6) 6 = 8 (14) (14) 6 = (8+1) (4+1) 46 = 9546.
В этом случае надо к первой цифре 8 прибавить 1, получим 9, далее 4+1 = 5; а последние цифры 4 и 6 оставляем без изменения. Получаем ответ 9546.
69 х 1111 = 6 (15) (15) (15) 9 = (6+1) (5+1) (5+1) 59 = 76659
76 х 1 111 111 = 7 (13)(13)(13)(13)(13)(13) 6 =
(7+1)(3+1)(3+1)(3+1)(3+1)(3+1) 36= 84444436
18) Умножение чисел на 101 , 1001 и т.д.
Чтобы любое число умножить на 101, надо к этому числу приписать справа это же число.
Примеры:
32 х 101 = 3232
47 х 101 = 4747
54 х 101 = 5454
93 х 101 = 9393
Чтобы трёхзначное число умножить на 1001, надо к этому числу справа приписать это же число.
Примеры:
324 х 1001 = 324 324
675 х 1001 = 675 675
869 х 1001 = 869 869
Другие примеры:
6478 х 10001 = 64786478
846932 х 1000001 = 846932846932
29) Умножение чисел на 37
Чтобы устно умножить число на 37, надо это число разделить на 3 и умножить на 111
Примеры:
24 х 37 = (24:3) х 37 х 3 = 8 х 111 = 888
18 х 37 = 18 : 3 х 111 = 6 х 111 = 666
20) Умножение на 1,5
Чтобы устно умножить число на 1,5 , прибавляют к множимому его половину.
Обоснование: а*1,5 = а*1+ а*0.5
Например:
34·1,5=34·1+34·0,5=34+17=51
23·1,5=23·1+23·0,5=23+11,5=34,5
21) Умножение на 1,25
Чтобы устно умножить число на 1,25 прибавляют к множимому его четверть.
Обоснование: а*1,25 = а*1+а*0,25
Например:
48·1,25=48·1+48·0,25=48+12=60
56·1,25=56·1+56·0,25=56+14=70
22) Умножение на 2,5
Чтобы устно умножить число на 2,5, к удвоенному числу прибавляют половину множимого.
Обоснование: а*2,5 = а*2+а*0,5
Например:
18·2,5=18·2+18*0,5 =36+9=45
39·2,5=39·2+39*0,5=78+19,5=97,5
23) Умножение на 0,75
Чтобы устно умножить число на 0,75, умножают число на 1,5 и делят пополам.
Обоснование: а*0,75 = (а*1,5)/2
Например:
30*0,75=30*1,5/2=45:2=22,5
24) Деление на 4
Чтобы устно разделить число на 4, его дважды делят пополам.
Обоснование: а:4 = а: (2·2)
Например:
76:4=38:2=19
236:4=118:2=59
25) Деление на 8
Чтобы устно разделить число на 8, его трижды делят пополам.
Обоснование: а:8 = а: (2·2·2)
Например:
464:8=232:4=116:2=58
516:8=258:4=179:2=64 ?
26) Деление на 5
Чтобы устно разделить число на 5, последнюю цифру в удвоенном числе отделяют запятой.
Обоснование: а:5 = 2*а/ 10
Например:
84:5=168:10=16,8
237:5=474:10=47,4
27) Деление на 15
Чтобы устно разделить число на 15, удвоенное число делят на 30.
Обоснование: а:15 = 2*а/ 30
Например:
240:15=480:30=48:3=16
462:15=924:30=308:10=30,8
28) Умножение и деление на 25
Для того, чтобы научиться устно умножать и делить на 25, надо хорошо знать признак делимости и таблицу умножения на 4. На 4 делятся те и только те числа, у которых две последние цифры числа выражают число, делящееся на 4:
Примеры:
124 делится на 4, так как 24 делится на 4;
1716 делится на 4, так как 16 делится на 4;
1800 делится на 4, так как 00 делится на 4.
Чтобы число умножить на 25, надо это число разделить на 4 и умножить на 100.
Примеры:
484 х 25 = (484 : 4) х 25 х 4 = 121 х 100 = 12 100; 124 х 25 - 124 : 4 х 100 - 3100.
Чтобы число разделить на 25, надо это число разделить на 100 и умножить на 4.
Примеры:
12 100 : 25 = 12 100 : 100 х 4 = 484; 3100:25 = 3100:100x4 = 124.
29) Умножение и деление на 75
Чтобы число умножить на 75, надо это число разделить на 4 и умножить на 300.
Примеры:
32 х 75 = (32 : 4) х 75 х 4 = 8 х 300 = 2400; 48 х 75 = 48 : 4 х 300 = 3600.
Чтобы число разделить на 75, надо это число разделить на 300 и умножить на 4.
Примеры:
2400:75 = 2400:300x4 = 32; 3600 : 75 = 3600 : 300 х 4 = 48.
30) Деление на 50
Чтобы устно разделить число на 50, его нужно разделить на 100 и умножить на 2.
Обоснование: а/50=а/100*2
Например:
21600:50=21600:100·2=216·2=432
8600:50=8600:100·2=86·2=172
31) Деление на 1,5
Чтобы устно разделить число на 1,5, удвоенное число делят на 3.
Обоснование: а/1,5 = 2*а/ 3
Например:
36: 1,5=72:3=24
53: 1,5=106:3=35,3
32) Деление на 0,5
Чтобы устно разделить число на 0,5 , его умножают на 2.
Обоснование: а/0,5 = а*2
Например:
27: 0,5 =27·2=54
85: 0,5=85·2=170
33) Деление на 0,25
Чтобы устно разделить число на 0,25 , его умножают на 4.
Обоснование: а/0,25= а*4
Например:
36/0,25=36·4=144
73/0,25=73·4=292
34) Деление на 0,75
Чтобы устно разделить число на 0,75 ,его умножают на 4 и делят на 3.
Обоснование: а/0,75= (а*4)/3
Например:
15/0,75 =15·4: 3=60:3=20
47/0,75 =47·4:3=188:3=62,6
35) Вычисление по формулам сокращенного умножения
1.Квадрат суммы двух величин равен квадрату первой плюс удвоенное произведение первой на вторую плюс квадрат второй.
(a+b)2=a2+2ab+b2
Например:
412 = (40+1)2 = 402 + 2 · 40 · 1 + 12 = 1600 + 80 + 1 = 1681
2.Квадрат разности двух величин равен квадрату первой минус удвоенное произведение первой на вторую плюс квадрат второй.
(a-b)2=a2-2ab+b2
Например:
982 = (100 - 2)2 = 1002 - 2 · 100 · 2 + 22 = 10000 - 400 + 4 = 9604
3.Произведение суммы двух величин на их разность равно разности их квадратов.
(a+b)(a-b)=a2-b2
Например:
(100 - 1)(100+1)=1002-12=9999
4.Куб суммы двух величин равен кубу первой плюс утроенное произведение квадрата первой на вторую плюс утроенное произведение первой на квадрат второй плюс куб второй.
(a+b)3=a3+3a2b+3ab2+b3
Например:
(8+5)3=83+3·82·5+3·8·52+53=512+960+600+125=2197
5.Куб разности двух величин равен кубу первой минус утроенное произведение квадрата первой на вторую плюс утроенное произведение первой на квадрат второй минус куб второй.
(a-b)3=a3-3a2b+3ab2-b3
Например:
(8-5)3=83-3·82·5+3·8·52-53=512-960+600-125=27
6. Произведение суммы двух величин на неполный квадрат разности равно сумме их кубов.
(a+b)(a2-ab+b2)=a3+b3
Например:
(3+4)(32-3·4+42)=33+43
7. Произведение разности двух величин на неполный квадрат суммы равно разности их кубов.
(a-b)(a2+ab+b2)=a3-b3
Например:
(5-4)(52+5·4+42)=53-43
36) Числа 1, 5, 6, 25, 76
Всякие числа, оканчивающиеся на 1, 5, 6, 25, 76 в любой степени будут оканчиваться ими же.
Например:
52=25
815723=…5
4919876543256=……….1
5763=191 102 976
1.3 Признаки делимости
Признак делимости на 2. Число делится на 2 тогда и только тогда, когда его последняя цифра делится на 2. Число, делящееся на 2, называется чётным, не делящееся на 2 – нечётным.
Признак делимости на 3. Число делится на 3, если сумма чисел, образованных его цифрами в десятичной записи делится на 3.
Признак делимости на 4. Число делится на 4 тогда и только тогда, когда две его последние цифры – нули, либо когда двузначное число, образованное двумя его последними цифрами, делится на 4.
Признак делимости на 5. Число делится на 5 тогда и только тогда, когда его последняя цифра – 5 или 0.
Признак делимости на 6. На 6 делятся все те и только те числа, которые одновременно делятся на 2 и на 3. С помощью этого признака можно установить, например, что число 721314 делится на 6, поскольку оно делится на 2 (оно четно) и на 3 (сумма его цифр делится на 3).
Признак делимости на 8.Число n делится на 8 тогда и только тогда, когда на 8 делится трехзначное число, образованное из трех последних цифр числа n.
Если внимательно рассмотреть признаки делимости на 2,4,8, то можно найти признак делимости на 2ª( a=1,2,3,4… ).Число n делится на 2ª тогда и только тогда, когда на 2ª делится a – значное число, которое образуют a последних цифр числа n. Действительно, исходное число n можно представить в виде суммы двух слагаемых: одного, оканчивающегося a нулями, и другого, образованного из a последних цифр числа n.Первое слагаемое делится на 10ª ,а значит, на 2ª , поскольку 10ª =5ª![]() 2ª . Таким образом, вопрос о делимости на 2ª исходного числа всецело зависит от делимости на 2ª второго слагаемого .
2ª . Таким образом, вопрос о делимости на 2ª исходного числа всецело зависит от делимости на 2ª второго слагаемого .
Признак делимости на 9. Число делится на 9 тогда и только тогда, когда сумма его цифр делится на 9.
Признаки делимости на 10, 100, 1000. Число делится на 10 тогда и только тогда, когда его последняя цифра – 0. Число делится на 100 тогда и только тогда, когда две его последние цифры – нули. Число делится на 1000 тогда и только тогда, когда три его последние цифры – нули.
Признак делимости на 11. Если из суммы всех цифр, стоящих на нечетных местах, вычесть сумму всех цифр, занимающих четные места, и в разности получится 0 либо число, кратное 11, то и испытуемое число кратно 11.
Например, 87 635 064:
8+6+5+6=25
7+3+0+4=14
25-14=11 – число кратно 11
Признак делимости на 11. Испытуемое число следует разбить на грани справа налево по две цифры и сложить их. Если полученная сумма делится без остатка на 11, то и испытуемое число кратно 11.
Например, 528
5+28=33 – число кратно 11
Объединенный признак делимости на 7, 11 и 13.
Число делится на 7, 11 или 13, если алгебраическая сумма чисел, образованных тройками цифр данного числа в десятичной записи с чередующимися знаками делится соответственно на 7, 11 или 13.
Доказательство. Заметим, что произведение чисел 7, 11 и 13 равно 1001. Поэтому число 1000 при делении на 7, 11 или 13 равноостаточно с –1. Далее поступаем как и в признаке делимости на 11.
Признак делимости на 19. Число делится без остатка на 19 тогда и только тогда, когда число его десятков, сложенное с удвоенным числом единиц, кратно 19.
Признак делимости на 25. Число делится на 25 тогда и только тогда, когда две его последние цифры либо нули, либо образуют число, делящееся на 25.
Признак делимости на 37. Число делится на 37, если сумма чисел, образованных тройками цифр данного числа в десятичной записи делится соответственно на 37.
Свойства делимости:
Теорема 1 (теорема о делимости суммы).
Если каждое слагаемое делится на некоторое число, то и сумма делится на это число.
Доказательство:
Пусть 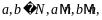
т.е.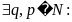
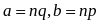
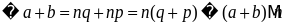 ,ч.т.д.
,ч.т.д.
Теорема 2 (теорема о делимости произведения). Если в произведении хотя бы один из множителей делится на некоторое число, то и произведение делится на это число.
Доказательство: Рассмотрим для двух множителей (для большего числа аналогично).
Пусть 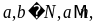
т.е. 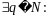
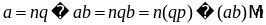 ,
,
ч.т.д.
1.4 Алгоритмы ускоренных вычислений
1)Алгоритм возведения в квадрат двузначных и трёхзначных чисел, оканчивающихся на 5.
![]()
![]() Чтобы возвести в квадрат число, оканчивающееся цифрой 5 (например, 65), умножают число его десятков (6), на число десятков увеличенное на 1 (на 6+1 = 7), и к полученному числу приписывают 25 (6 х 7=42. Ответ: 4225).
Чтобы возвести в квадрат число, оканчивающееся цифрой 5 (например, 65), умножают число его десятков (6), на число десятков увеличенное на 1 (на 6+1 = 7), и к полученному числу приписывают 25 (6 х 7=42. Ответ: 4225).
2)Возведение в квадрат чисел состоящих только из 1.
11 х 11 =121
111 х 111 = 12321
1111 х 1111 = 1234321
11111 х 11111 =123454321
111111 х 111111 = 12345654321
1111111 х 1111111 = 1234567654321
11111111 х 11111111 = 123456787654321
111111111 х 111111111 = 12345678987654321
3) Алгоритм возведения в квадрат чисел, близких к 50.
1) вычесть из этого числа 25;
2) приписать к результату двумя цифрами квадрат избытка этого числа над 50.
Примеры:
582 = 3364
Пояснение. 58 – 25 = 33, 82 = 64, 582 = 3364.
642 = 4096
Пояснение. 64 – 25 = 39, 64 – 50 = 14, 142 = 196, 642 = 3996 = 4096.
4)«Интересные» числа с применением свойств умножения
Число - 142857
Попробуем это число умножить на 1, 2, 3, 4, 5, 6
142 857 х 1 = 142 857; 142 857 х 4 = 571 428;
142 857 х 5 = 714 285; 142 857 х 2 = 285 714;
142 857 х 6 = 857 142; 142 857 х 3 = 428 571;
5) Интересные цифры
Возьмите числа, кратные трём,- от 3 до 2,умножьте их на 3 . Произведения трёхзначные. В каждом из них три раза повторяется то число, которое получится, если множимое разделить на 3 :
3 х 37 = 111 33 х 3367 = 111111
6 х 37 = 222 66 х 3367 = 222222
9 х 37 = 333 99 х 3367 = 333333
12 х 37 = 444 132 х 3367 = 444444
15 х 37 = 555 165 х 3367 = 555555
18 х 37 = 666 198 х 3367 = 666666
21 х 37 = 777 231 х 3367 = 777777
24 х 37 = 888 264 х 3367 = 888888
27 х 37 = 999 297 х 3367 = 999999
6) Извлечение корня
Алгоритмы извлечения квадратного корня из чисел методом «в столбик».
Извлечение квадратного корня из целого числа «нацело».
Пример: найдём 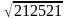 .
.
| № | Шаги алгоритма | Пример | Комментарии |
| 1 | Разбить число на группы по 2 цифры в каждой справа налево | 21’ 25’ 21 | Общее число образовавшихся групп определяет количество цифр в ответе |
| 2 | Для первой группы цифр подобрать цифру, квадрат которой будет наибольшим, но не превосходящим числа первой группы | 1 группа – 21 42=16 16 цифра - 4 | Найденная цифра записывается в ответе на первом месте |
| 3 | Из первой группы цифр вычесть найденный на шаге 2 квадрат первой цифры ответа | _21’ 25’ 21 16 5 |
|
| 4 | К остатку, найденному на шаге 3, приписать справа (снести) вторую группу цифр | _21’ 25’ 21 16__ 525 |
|
| 5 | К удвоенной первой цифре ответа приписать справа такую цифру, чтобы произведение полученного в результате числа на эту цифру было наибольшим, но не превосходила числа, найденного на шаге 4 | 4*2=8 цифра – 6 86*6=516 516 | Найденная цифра записывается в ответе на втором месте |
| 6 | Из числа, полученного на шаге 4 вычесть число, полученное на шаге 5. Снести к остатку третью группу | _21’ 25’ 21 16 _525 516 921 |
|
| 7 | К удвоенному числу, состоящему из первых двух цифр ответа, приписать справа такую цифру, чтобы произведение полученного в результате числа на эту цифру был наибольшим, но не превосходило числа, полученного на шаге 6 | 46*2=92 цифра 1 921*1=921 | Найденная цифра записывается в ответе на третьем месте |
| 8 | Записать ответ | √212521=461 |
|
Извлечение квадратного корня из целого числа (корень не извлекается «нацело»)
Пример: найдём 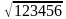 .
.
| № | Шаги алгоритма | Пример | Комментарии |
| 1 | Установить точность извлечения 1/10m | m = 3 | Определить количество знаков в ответе после запятой |
| 2 | Разбить число на группы по 2 цифры в каждой справа налево | 12’ 34’ 56 |
|
| 3 | Создать группы в дробной части числа, приписав, справа нули | 12’ 34’ 56’, 00’ 00’ 00 | Количество приписываемых нулей сокращается с заявленной точностью. В нашем примере – 6 нулей (3 группы, так как m=3) |
| 4 | Использовать алгоритм 1, начиная со 2 шага | √12”34”56”00”00”00=351,363 _9_ _334 325 _956 701 _25500 21069 443100 421596 _2150400 2108169 42231 |
|
Извлечение кубического корня
Многие из нас знают метод извлечения корней разложением числа на простые множители. Рассмотрим метод быстрого извлечения кубического корня. Для успешного овладения этой методикой необходимо запомнить несколько ключевых цифр таблицы кубов однозначных чисел.
| N | 13 | 23 | 33 | 43 | 53 | 63 | 73 | 83 | 93 |
| N2 | 1 | 8 | 27 | 64 | 125 | 216 | 343 | 512 | 729 |

 В правой части числа оканчиваются цифрами от 1 до 9. Надо запомнить, какое цифровое окончание соответствует каждому основанию левой части. Обратим внимание на то, что цифры 1,4,5,6,9 в своем кубе оканчиваются на ту же цифру. В остальных случаях последняя цифра куба равна разности между 10 и числом, возводимым в куб. Тогда легко найдется цифра единиц корня.
В правой части числа оканчиваются цифрами от 1 до 9. Надо запомнить, какое цифровое окончание соответствует каждому основанию левой части. Обратим внимание на то, что цифры 1,4,5,6,9 в своем кубе оканчиваются на ту же цифру. В остальных случаях последняя цифра куба равна разности между 10 и числом, возводимым в куб. Тогда легко найдется цифра единиц корня.
Вычислим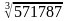 . Чтобы найти число десятков искомого двузначного числа, нужно обратить внимание на то, сколько тысяч в подкоренном числе. В нашем примере число тысяч 571, а в таблице имеем числа 512=
. Чтобы найти число десятков искомого двузначного числа, нужно обратить внимание на то, сколько тысяч в подкоренном числе. В нашем примере число тысяч 571, а в таблице имеем числа 512=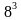 и 729=
и 729=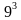 . Выберем число, куб которого наиболее близкий, но меньше числа 571. Следовательно, десятков будет 8. Оставшиеся цифры 787 оканчиваются 7, а так как
. Выберем число, куб которого наиболее близкий, но меньше числа 571. Следовательно, десятков будет 8. Оставшиеся цифры 787 оканчиваются 7, а так как 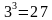 , то единиц будет 3. Итак,
, то единиц будет 3. Итак, 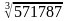 = 83.
= 83.
Применение на практике.
Из города А в город В, расстояние между которыми равно 300 км, выехал мотоциклист. Проехав 64% всего пути, он остановился на 18 мин для заправки горючим. Чтобы наверстать потерянное время, оставшуюся часть пути он проехал, увеличив скорость на 12 км/ч. С какой скоростью двигался мотоциклист после остановки?
|
До остан. | V,км/ч | t,ч | S,км |
| x |
|
300
108км | |
| После остан. | X+12 |
|
300*0,64=192(км) - путь до остановки;
300 – 192= 108(км) - путь после остановки;
Х(км/ч) – первоначальная скорость мотоциклиста;
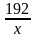 (ч) - время движения мотоциклиста до остановки;
(ч) - время движения мотоциклиста до остановки;
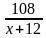 (ч) - время движения мотоциклиста после остановки;
(ч) - время движения мотоциклиста после остановки;
18 мин=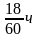 =
= - время остановки;
= 0
1080х+3х(х+12)-1080(х+12)=0
Х=0
Х=-12
1080х+
+36х-1080х-12960=0
+36х-12960=0 : 3
+12х-4320=0
Д= 144-4*(-4320)=144+17280= 17424
=
=132
Вычислим 1*2=2
=132
1
74
69
524
524
0 =
=60 (км/ч) - первоначальная скорость;
=
=-72 – не удовлетворяет условию задачи;
60+12=72(км/ч)- скорость мотоциклиста после остановки.
Ответ: 72 км/ч
7) Пифагоровы числа
Пифагоровы числа – бесчисленное множество целых положительных чисел a, b, c, удовлетворяющих соотношению a2+b2=c2
Свойства:
-Один из катетов должен быть кратным трем
-Один из катетов должен быть кратным четырем
-Одно из пифагоровых чисел должно быть кратным пяти
Пифагоровы числа имеют вид:
a=mn b=(m2-n2)/2 c=(m2+n2)/2
некоторые пифагоровы числа:
при m=3, n=1 32+42=52
при m=5, n=1 52+122=132
при m=7, n=1 72+242=252
при m=9, n=1 92+402=412
при m=11, n=1 112+602=612
8) Мгновенное умножение
Вычислители-виртуозы во многих случаях облегчают себе вычислительную работу, прибегая к несложным алгебраическим преобразованиям. Например, 9882 выполняется так:
988*988=(988+12)(988-12)+122=1000*976+144=978 144
В этом случае используется следующая формула:
a2=a2-b2+b2=(a-b)(a+b)+b2
1.5 Задачи
1) Номер автомашины
Прогуливаясь по городу, трое студентов-математиков заметили, что водитель автомашины нарушил правила уличного движения. Номер машины (четырехзначный) ни один из студентов не запомнил, но, так как они были математики, каждый из них приметил некоторую особенность этого четырехзначного числа. Один из студентов вспомнил, что две первые цифры числа были одинаковы. Второй вспомнил, что две последние цифры также совпадали между собой. Наконец, третий утверждал, что все это четырехзначное число является точным квадратом. Можно ли по этим данным узнать номер машины?
Решение:
Обозначим первую и вторую цифру искомого числа через a, а третью и четвертую - через b. Тогда 1000a+100a+10b+b=1100a+11b=11(100a+b)
Искомое число делится на 11, так как число-точный квадрат, то оно делится и на 112.Значит 100a+b делится на 11. Используя признак делимости на 11 (если разбить испытуемое число на грани по два числа справа налево, то их сумма будет кратна 11)
Значит a+b делится на 11, так как a и b – однозначные числа, то a+b=11
Таким образом цифра b может принимать значения от 0 до 9, но так как искомое число является точным квадратом то для b подходят только значения 0, 1, 4, 5, 6, 9
для a подходят только значения 7, 6, 5, 2
Имеем:
b=4, a=7
b=5, a=6
b=6, a=5
b=9, a=2
Номер автомашины следует искать из чисел 7744, 6655, 5566, 2299
Последние три числа не являются точными квадратами, так как 6655 не делится на 25; 5566 делится на 2, но не делится на 4; 2299=121*19. Однако 7744: 44 делится на 4, значит и все число делится на 4.
7744=4*1936=4*4*484=22*22*222=882
Ответ:7744
2) Доплата
Однажды в старые времена произошел такой случай. Двое прасолов продали принадлежащий им гурт волов, получив при этом за каждого вола столько рублей, сколько в гурте было волов. На вырученные деньги купили стадо овец по 10 рублей за овцу и одного ягненка. При дележе поровну одному досталась лишняя овца, другой же взял ягненка и получил с компаньона соответствующую доплату. Как велика была доплата (в рублях)?
Решение
Стоимость стада в рублях есть точный квадрат, так как стадо приобретено на деньги от продажи n волов по n рублей за каждого. Одному из компаньонов досталась лишняя овца, следовательно, число овец нечетное, а значит, и число десятков в n2 так же нечетное.
Квадрат всякого числа из а десятков и b единиц равен: 100a2+20ab+b2=(10a2+2ab)*10+b2
10a2+2ab-четное число, так как делится на 2, поэтому b2-нечетное. Это квадрат цифры единиц, поэтому может принимать значения 0, 1, 4, 9, 16, 25, 36, 49, 64, 81.
Среди них нечетное число десятков имеют числа 16 и 36.
Значит 100a2+20ab+b2 будет оканчиваться на 6.
Теперь легко найти ответ на вопрос задачи. Ясно, что ягненок пошел за 6 рублей. Компаньон, которому он достался, получил, следовательно, на 4 рубля меньше. Чтобы уравнять долг, обладатель ягненка должен получить 2 рубля.
Ответ: доплата равна 2 рублям
Глава 2. Практическая часть
Было проведено два опроса, в которых участвовало 25 человек (возрастная категория 16-17 лет). В первом случае, ученики не были ознакомлены с приемами устного счета, во втором случае мы кратко рассказали о самых интересных и удобных приемах устного счета, затем провели похожий на первый опрос.
Опрос 1
| 32 х 111 = |
| 947 х 1001 = |
|
| 168:5 = |
| 12100:25 = |
|
| 582 = |
| 36: 1,5 = |
|
| 87 635 064-кратно ли 3/4/11/13/19/25/37 |
| 6 486 117-кратно ли это число 3/4/9/11/13/19/37 |
|
| 65 х 10101 = |
| √123456 = |
|
| √110889 |
| 1111 х 1111 = |
|
| 111 х 111 |
| 645·11 = |
|
| 69 х 37 |
| 1252 = |
|
Опрос 2
| 99 х 1010101 = |
| 1001 х 101 = |
|
| 11111 х 11111 = |
| 11111 х 1111 = |
|
| 592 = |
| 612 = |
|
| 34 762 816 -кратно ли 3/4/9/11/13/19/25/37 |
| 583 447 117-кратно ли это число 3/4/9/11/13/19/37 |
|
| 577 х 11= |
| √731 025 = |
|
| √311 364 = |
| 788 х 11 = |
|
| 377 : 5 = |
| 377 : 25 = |
|
| 198 : 1,5 = Доп вопрос 288 : 0,25 = |
| 288 : 1,5 = Доп вопрос 388 : 0,25 = |
|
Результаты опроса
| Вид | Правильные ответы (%)-1 | Правильные ответы (%)-2 |
| Деление на 1,5 | 70 | 65 |
| Умножение на 101, 1001 | 0,64 | 83 |
| Деление на 5, 25 | 0,92 | 81 |
| Извлечение кв. корня | 4 | 61 |
| Умножение на 11, 111 | 84 | 74 |
| Возведение числа в кв. | 64 | 87 |
| Умножение 111 х 111 | 72 | 91 |
| Кратность На 3 На 4 На 9 На 11 На 13 На 19 На 25 На 37 | 44 60 38 8 28 32 58 24 | 70 87 70 70 52 52 75 48 |
По результатам опроса, наиболее эффективными оказались приемы определения кратности чисел и извлечения квадратного корня.
Практически в каждом действии наблюдается положительная динамика. Таким образом, можно сделать вывод, что приемы устного счета являются эффективными и значительно увеличивают вероятность того, что пример будет решен правильно
Заключение
Устные вычисления дают возможность не только быстро производить расчеты в уме, но и контролировать, оценивать, находить и исправлять ошибки в результатах вычислений. Приемы устного счета помогут значительно упростить решение тех или иных задач, сократить время решения. При этом освоение вычислительных навыков развивает память и помогает людям в различных сферах жизни.
В данной работе были описаны различные приемы устного счета и доказана их эффективность на основе проведенного опроса.
И свою работу мы хотим завершить словами Гёте: «Счет является, правда, низкой, но уже идеальной деятельностью человека, и с помощью него столь многое осуществляется в обыденной жизни»
Кордемский Б.А., Ахадов А.А. Удивительный мир чисел: Книга учащихся,- М. Просвещение, 1986г.
Билл Хэндли «Считайте в уме как компьютер», Минск, Попурри, 2009г.
Александр Наниев «Математика для всех», Владикавказ ,2008г.
.

 Получите свидетельство
Получите свидетельство Вход
Вход



 192км
192км








 Методическая разработка "Подготовка к ЕГЭ по математике" (99.29 KB)
Методическая разработка "Подготовка к ЕГЭ по математике" (99.29 KB)
 0
0 79
79 0
0 Нравится
0
Нравится
0


