Механик масалаларда уч каррали интеграллар

mexanik masalalarDA Uch karrali integrallar

¹Mirmuxamedov Djuman Xazratkulovich

¹Umarov Xabibullo Raxmatullayevich

²Abduxoliqov Umidjon G‘ulomqodir o‘g‘li

¹Guliston davlat universiteti Matematika kafedrasi katta o‘qituvchisi, Guliston, O‘zbekiston

²Guliston davlat universiteti Matematika yo‘nalishi iqtidorli talabasi, Guliston, O‘zbekiston

Mazkur tadqiqot ishida, geometrik va fizik masalalarni uch karrali integral yordamida oson usullarda yechish, geometrik isbotlashlarda qulayliklar yaratish masalasi koʻrib chiqilgan. Uch karrali integralning nazariy asoslari va ularning geometrik va fizik masalalarga tadbiqlari oʻrganilgan.

Tabiiyki, barcha geometrik va mexanik kattaliklar fazodagi 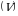jismning massasiga bogʻliqdir. Bunday holni uch karrali integral orqali ifodalaymiz [2, 3].

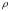orqali 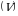jismning ixtiyoriy nuqtadagi zichligini belgilaylik: u nuqtaning koordinatalarini funksiyasi boʻladi va bu funksiyani har doim uzluksiz deb faraz qilamiz. 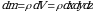massa elementlarini yigʻib chiqamiz va barcha massa kattaliklar uchun

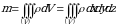(1)

ega boʻlamiz.

Elementar statistik momentlar uchun ushbu

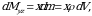
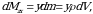
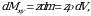
munosabatlar oʻrinli boʻlishini topamiz. Statistik momentlarni topish formulasi

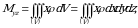
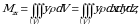(2)

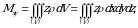
iborat boʻladi.

Ogʻirlik markazining koordinatalari uchun

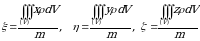(3)

formulalar oʻrinli boʻladi.

Bir jinsli jism uchun 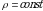boʻladi va ogʻirlik markazining koordinatalari uchun

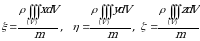(4)

munosabatlar oʻrinli boʻladi.

Koordinata oʻqlariga nisbatan inersiya momentlari uchun

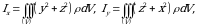
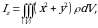(5)

formulalar oʻrinli boʻladi.

Koordinata tekisliklariga nisbatan inersiya momentlari

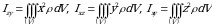(6)

formulalar bilan hisoblanadi.

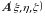nuqtada mahkamlangan 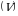jism massa bilan tuldirilgan boʻlsin. 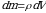massa elementi tomoni nisbatan tortishish kuchi koordinata oʻqlarida proeksiyaga ega boʻladi.

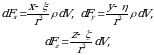
bu yerda 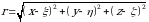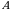nuqtadan 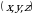nuqtagacha masofa elementi. Bundan toʻliq 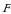tortishish kuchini koordinata oʻqlaridagi proeksiyasi uchun

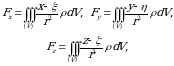(7)

ega boʻlamiz [2, 4].

Xuddi shunday 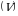jismning nuqtadagi potensiali ham

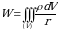(8)

formula bilan hisoblanadi [3, 4].

Agar 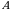nuqta jismdan tashqarida boʻlsa, bu integrallarning barchasi xos integrallar boʻladi. Bu holda 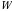integralni ixtiyoriy 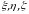oʻzgaruvchilar boʻyicha integral ostida differensiallash mumkin. Natijada

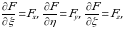(9)

hosil qilamiz.

Agar 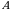nuqta 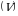jismga tegishli boʻlsa, bu nuqtada 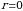va (7) va (8) dagi integral ostidagi funksiyalar chegaralanmagan boʻlib qoladi. Keyinroq bu integrallarni xosmas ekanligini va mavjudligini (9) munosabatning bajarilishini koʻrsatamiz.

Uch karrali integrallarning mexanikaga tadbiqlariga doir ba’zi bir misollar koʻrib chiqaylik.

1 – misol. 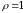boʻlganda ikki oʻlchovli holda bir jinsli silindrik brusning statistik momenti uchun

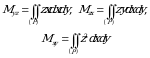
formulaga egamiz. Bularga (2) formulalarni qoʻllab:

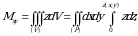
bu yerda

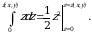
2 – misol. 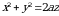paraboloid va 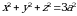sferik sirtlar bilan chegaralangan jismning ogʻirlik markazini toping.

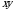tekislikka nisbatan statistik momenti 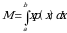formulada ni bilan almashtirib hisoblash mumkin. Koʻndalang kesim 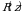ning yuzi 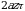ga teng. 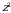funksiya 0 dan va 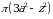funksiya uchun, yoki oʻzgaruvchi dan 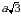gacha oʻzgaradi. Shunday qilib,

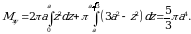
Shuningdek jismning hajmi ma’lum: 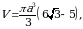[4] boʻlsa,

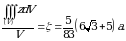
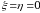simmetrik jism boʻlgani uchun.

3 – misol. 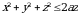sferaning massasini toping va ogʻirlik markazining oʻrnini aniqlang.

Agar sferaning nuqtalari zichligi bu nuqtalar bilan koordinata boshigacha boʻlgan masofaga teskari proporsianal boʻlsa,

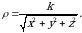
(1) formulaga koʻra massa

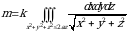
teng.

Bu uch karrali integralda almashtirish bajarib, uni ushbu

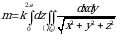
sodda integral va ikki karrali integrallar orqali ifodalash mumkin. Bu yerda 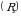radiusi 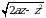ga teng boʻlgan aylana. Ichki integralni qutb koordinatalarga oʻtib

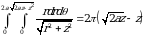
tengligini topamiz.

Bundan esa 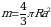boʻlishini topamiz.

Statistik momenti esa (2) munosabatlardan foydalanib

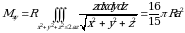
tengligini topamiz.

Ogʻirlik markazi esa, 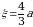ga teng, qolgan ikki koordinatasi 0 ga teng.

ADABIYOTLAR ROʻYXATI

1. Г.Фихтенгольц. «Курс дифференциального и интегрального исчисления», Том I, II, III. Москва, «Физматлит», 2001.

2. Sh.O.Alimov, R.R.Ashurov. Matematik analiz 1,2,3 q. T. «Mumtoz soʻz», 2018.

3. A.Sa’dullayev, H.Mansurov, G.Xudoyberganov, A.Vorisov, R.Gʻulomov «Matematik analiz kursidan misol va masalalar toʻplami», 1-, 2- tom, Toshkent, «Oʻzbekiston» – 1993, 1996.

4. Б.П. Демидович, «Сборник задач и упражнений по математическому анализу», Изд. 13-е, Москва, «ЧеРо», 1997.