Математика на протяжении всей истории человечества является одной из основных составных частей человеческой культуры, ключом к познанию и адекватной оценке окружающего мира. Математическое образование является неотъемлемой частью гуманитарного образования в широком понимании этого слова, одним из основных элементов формирования личности.
Математика является основной, а часто и основополагающей частью общего образования. Ни одна область человеческой деятельности не может обходиться без математики. Школьное математическое образование способствует: овладению конкретными знаниями, необходимыми в современном мире; приобретению навыков логического алгоритмического мышления; развитию способности объективной оценки окружающего мира, формированию ответственности; воспитанию способности к адекватному и объективному восприятию окружающего мира.
Важную роль в учебном процессе играют формы и/или виды обучения, в качестве которых выступают устойчивые способы организации педагогического процесса.
Формы обучения – виды учебных занятий, способы организации учебной деятельности школьников, учителя и учащихся, направленные на овладении учащимися знаниями, умениями и навыками, на воспитание и развитие их в процессе обучения. Основной формой организации учебно-воспитательной работы в школе является урок.
Урок – форма организации обучения с целью овладения учащимися изучаемым материалом (знаниями, умениями, навыками, мировоззренческими и нравственно-эстетическими идеями).
К основным видам уроков относятся:
комбинированный урок
урок изложения нового материала
урок закрепления изучаемого материала и выработки практических умения и навыков
урок самостоятельной работы;
урок повторения, обобщения и систематизации изучаемого материала;
урок проверки и оценки и систематизации изучаемого материала;
урок проверки и оценки знаний, умения и навыков;
интегрированный урок и т.д..
Повысить вероятность интереса – создать необходимую атмосферу увлеченности. Значительное влияние на развитие математических способностей оказывают коллективные обсуждения и работы. Ввиду этого можно применять специальные уроки: уроки в компьютерном классе, урок вычисления на счётных приборах, кино-урок, математический бой и другие.
Понижение интереса к учебному материалу учениками зачастую объясняется неспособностью учащихся в силу своего возраста или степени подготовленности, а также по причине завышенной самооценки воспринимать предлагаемые задачи как действительно необходимые для решения в повседневной жизни. Отсутствие опыта работы и решения жизненных задач играет не в пользу учащегося, учащиеся часто делятся на две группы (с разной степенью проявления). Малая часть учащихся воспринимает процесс изучения как действительно необходимый на текущее время (мотивация такого поведения мы оставим за рамками данной работы). Основная часть учащихся относится к обучению поверхностно, одна группа считает что со временем они всему научаться (“ни чего сложного там нет”), вторая группа считает что все что необходимо они изучат потом (“выучим только то что будет нужно”). Прошло время, когда все мечтали стать космонавтами, на данном этапе подрастающее поколение в основной своей части стремится стать бизнесменами. И это нужно отметить уже более обдуманная позиция. Каждый из учащихся в ой или иной мере строит планы по развитию своего бизнеса (из бесед с учащимися можно активно подбирать варианты учебного бизнеса).
Применяемые в обучении бизнес цепочки должны иметь реальную ненадуманную последовательность действий, учащиеся должны не только решать отдельные задачи. Но и понимать их взаимосвязь. Учащиеся должны дорожить правильным решением каждой задачи. Неудовлетворительные оценки по итогам решения таких задач недопустимы. Задания изначально строятся с высоким уровнем сложности и их основная задача “встряхнуть” учащихся. Разбор неправильных решений может наглядно показать цену даже самой маленькой ошибки.
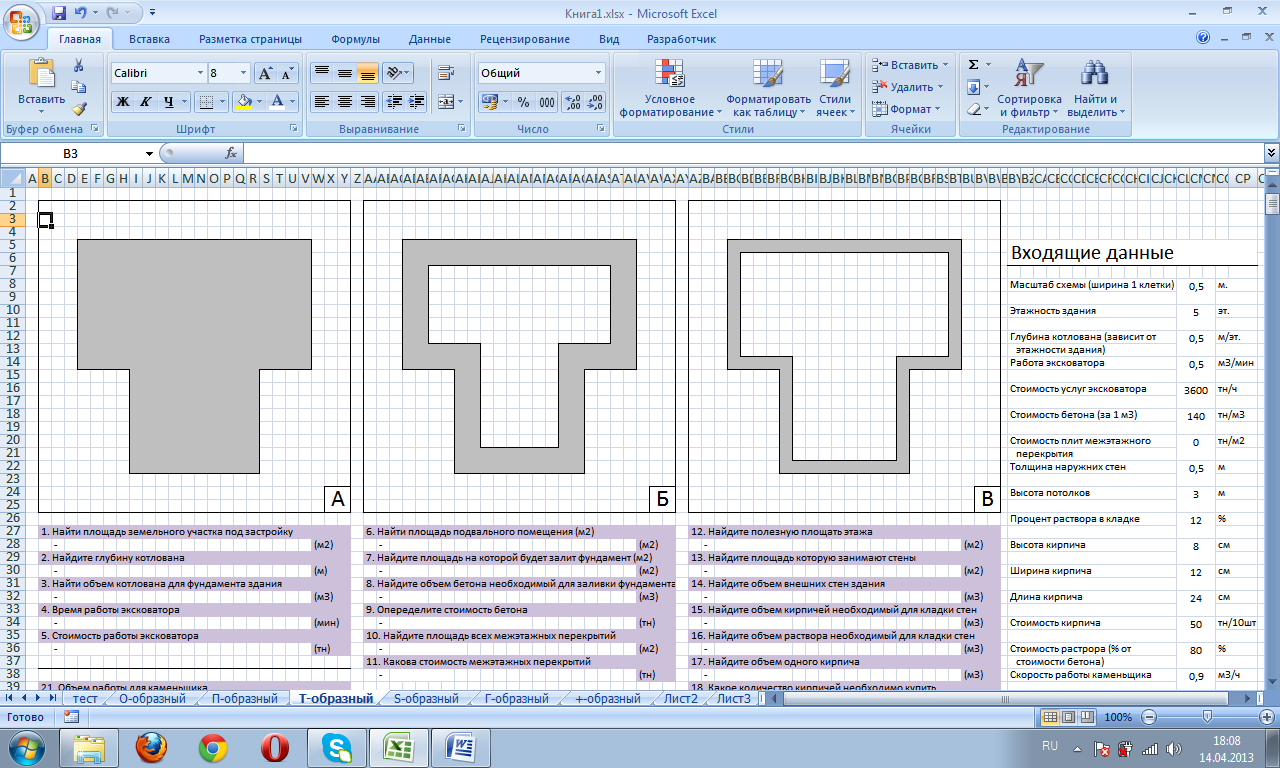
Как пример такого урока можно организовать и провести урок «Строим дом». Метод выполнения задания может быть как групповой, так и индивидуальный, иметь контрольные или ознакомительные цели, а также служить основой проектной работы учащегося.
Предварительная подготовка имеет большое значение и позволяет увеличить коэффициент отдачи от учебного времени, за счёт сокращения записей и переноса информации в тетради. Для групп учеников или индивидуально каждому выдаются задания, в виде масштабных схем, на расчёт постройки дома, высоких уровнях усвоения материала, могут применяться проектные работы учеников по собственным схемам.
Задание расчёта «СТРОИМ ДОМ» может состоять из следующих задач (входные параметры могут определяться учителем или самостоятельно учащимися по мере проведения урока):
расчёт по схеме площади строящегося дома;
определение этажности дома;
расчёт котлована под фундамент;
расчёт количества часов работы экскаватора;
расчёт стоимости работы экскаватора;
расчёт подвального помещения и фундамента здания;
расчёт потребности в бетоне для фундамента;
рассчитываем стоимость бетона;
рассчитываем площадь необходимых междуэтажный перекрытий;
рассчитываем объем кирпичей и раствора для стен здания;
вычисляем полезную площадь здания;
расчёт площади занимаемой стенами;
определение количества раствора и кирпичей для стен здания;
расчёт требуемого количества раствора для необходимого объёма кирпичей;
вычисляем стоимость кирпичей и раствора;
вычисляем объем работы каменщика;
вычисляем заработную плату каменщика;
рассчитываем время строительства и количество рабочих;
рассчитываем стоимость дома.
Задания могут усложняться как путём введения сложных входных данных, так и путем постановки дополнительных задач по анализу создаваемой математической модели. Создаваемые таким образом математические модели могут использоваться и при реализации других учебных дисциплин, а их анализ позволит ученикам усвоит описанные в них взаимосвязи и понять степень их взаимодействия.
Решение задач может быть различным по степени фиксации процесса, от записи всех формул, вычислений и полученных ответов, до сведения решения задачи к выдаче итогового ответа.
На первоначальном этапе рассмотрения и создания таких моделей. А также при значительных различиях в степени усвоения материала учащимися, рекомендуется производить полную фиксацию математической модели на специальных бланках.
Учащиеся на таких уроках находят пути решения интересных задач, развивают математическую речь, приобретают навыки составления задач самостоятельно, умения слушать и воспринимать работы товарищей, способности задавать вопросы по существу. Учащиеся с удовольствием работают в группах, советуются между собой, обмениваются мнениями.
Применение полученных знаний при решении практических задач есть цель обучения. Полученные знания не могут принести пользу учащемуся, если он не сможет их применить в жизни. Решение отдельных задач позволяет учащемуся совершенствовать свою «инструментальную» базу. Решение последовательных задач позволяет вникнуть в особенности «инструментария» и изучить различные методики его применения.
При решении последовательных задач учащиеся развивают свои компетентностные способности, создают математические модели, которые могут совершенствоваться ими по мере обучения. Чем реальнее будут поставленные задачи, тем более полноценные знания получат обучаемые, как в области математики, так и по другим предметам обучения.
Применение при создании математических моделей компьютерной техники позволяет учителю повысить скорость проверки принятых учащимися решений, а учащимся расширить свои аналитические способности в области исследования математических моделей. Создание и совершенствование математических моделей позволит учащимся в будущей своей учёбе более качественно осваивать вопросы программирования.
Применение последовательных и взаимосвязанных задач позволит учащимся постигать окружающий их мир и приносить посильную по способностям пользу семье и обществу.
Приложение
Входящие данные:
Стоимость услуг экскаватора 3600 тн/ч. Стоимость бетона (за 1 м3) 140 тн/м3. Стоимость плит межэтажного перекрытия 0 тн/м2. Толщина наружных стен 0,5 м. Высота потолков 3 м. Процент раствора в кладке 12 %. Высота кирпича 8 см. Ширина кирпича 12 см
Длина кирпича 24 см. Стоимость кирпича 50 тн/10шт. Стоимость раствора 80 % от стоимости бетона. Скорость работы каменщика 0,9 м3/ч. Каменщик за час работы требует оплату 1200 тн/ч. Количество нанятых каменщиков 3 чел. Количество рабочих часов в день 8 ч. Сколько выходных в неделю 2 дн.
Весь материал – смотрите документ.

 Получите свидетельство
Получите свидетельство Вход
Вход











 Методы и формы обучения математике (0.18 MB)
Методы и формы обучения математике (0.18 MB)
 0
0 5669
5669 944
944 Нравится
0
Нравится
0


