МЕТОД МАЖОРАНТ (МЕТОД ОЦЕНКИ)
Этим методом можно решать нестандартные уравнения; уравнения повышенной сложности, например, уравнения в левой и правой части которой находятся функции, имеющие различную природу; уравнения или системы уравнений, в которых количество переменных превышает количество уравнений; задачи с параметром. Метод мажорант также называют методом оценки левой и правой частей, входящих в уравнения и неравенства. Применение метода оценок будет успешным, если мы умеем находить экстремумы элементарных функций, область значений, исследовать функцию с помощью производной.
.
Определение. Мажорантой данной функции f(х) на множестве Р, называется такое число М, что либо f(х) ≤ М для всех х ϵ Р, либо f(х) ≥ М для всех х ϵ Р.
Термин «мажоранта» происходит от французского слова «majorante», от «majorer» — объявлять большим.
Мажоранты многих элементарных функции известны. Их нетрудно указать, зная область значений функции. Приведем примеры функций, мажоранты которых хорошо знаем.
Пример 1: f(x)= sin x.
-1 ≤ sin x ≤ 1.
М = –1, М =1
Пример 2: f(x)= cos x
-1 ≤ cos x ≤ 1.
М = –1, М.= 1
Пример 3: f(x)= ах2 + bx + с
(m, n) – координаты вершины параболы. n = f(m). Мажоранта квадратичной
функции - ордината вершины. М = n.
М = (4ас–b2) / 4а.
Пример 4: f(x)= |x|
По определению |x| ≥ 0 М= 0
Пример 5. у =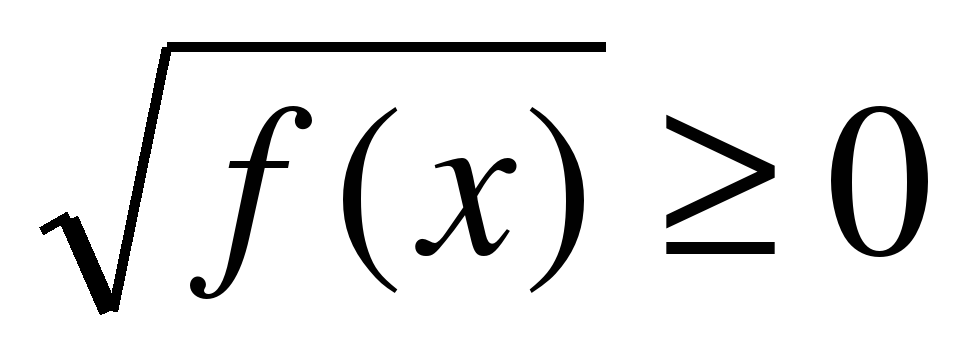 М.=0
М.=0
Пример 6: Найдем мажоранту функции 
Ее область определения является 
И для всех  поэтому g(x) ≤ 3.
поэтому g(x) ≤ 3.

Значит
Основная идея метода мажорант состоит в следующем:
Пусть мы имеем уравнение  и существует такое число М, что для любого х из области определения
и существует такое число М, что для любого х из области определения  имеем
имеем  . Тогда уравнение
. Тогда уравнение  равносильно системе
равносильно системе 
Метод мажорант:
- Оценить левую часть
- Оценить правую часть
- Составить систему уравнений
- Сделать вывод
- Выполнить проверку
4. Решить уравнение 
Решение
g(x)= х2 – 6х + 11
g(x) = (x – 3)2 + 2; D(g) = R, g(x) ≥ 2.

Найдем мажоранту функции f(x) с помощью производной:

D(f') = (2; 4).
Найдем критические точки:
3 — внутренняя точка D(f) и f'(3) = 0, следовательно, 3 — критическая точка.
Непрерывная на данном отрезке функция имеет единственный экстремум, он максимум, значит, это наибольшее значение функции.
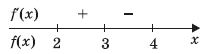


Решение этой системы х=3
Проверка: 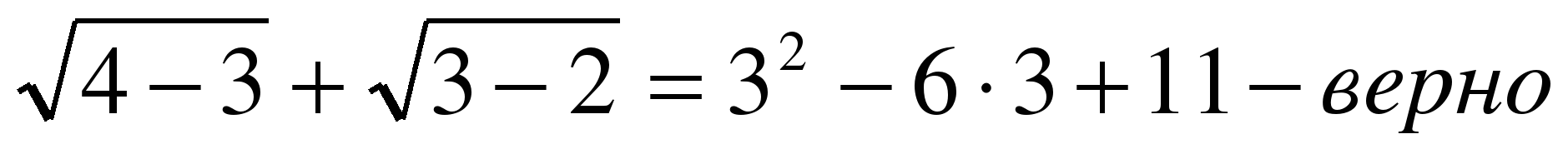
Ответ: x = 3
2. Решить уравнение 
Решение. Рассмотрим функции
f(x) = (x – 8)2 + 3, D(f) = R, f(x) ≥ 3. , D(g) = R.

Так как  для всех
для всех  поэтому g(x)≤3.
поэтому g(x)≤3.
Данное уравнение равносильно системе
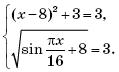
Число 8 — корень первого уравнения системы. Проверим, является ли оно корнем второго уравнения:

Значит, число 8 — решение системы.
Ответ: 8.
Пример 2.8. Найдите все значения параметра а при которых уравнение
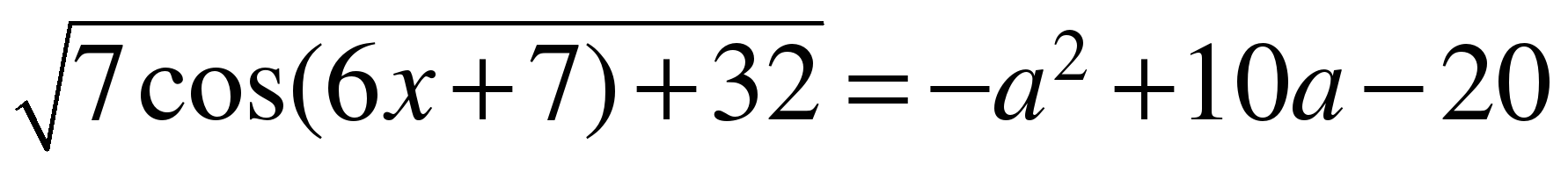 имеет решение.
имеет решение.
Решение.
Оценим обе части уравнения.
Н
айдем множество значений левой части исходного уравнения: так как , то , тогда, следовательно, наименьшее значение равно 5.
В правой части данного уравнения – квадратичная функция, графиком которой является парабола, ветви направлены вниз.
Выделив, полный квадрат получаем: . Следовательно, наибольшее значение правой части равно 5 и достигается в вершине при , то есть при .
Итак, исходное уравнение имеет решение при .
Ответ: 5.


 Получите свидетельство
Получите свидетельство Вход
Вход




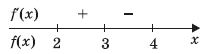

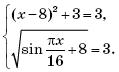









 Метод Мажорант (методический материал) (0.11 MB)
Метод Мажорант (методический материал) (0.11 MB)
 0
0 5581
5581 292
292 Нравится
0
Нравится
0








