Метод динамического программирования
Методическая разработка для учителей информатики
Вороков Аслан Анатолиевич
МБОУ СОШ с УИОП г. Салехард
2016 г.
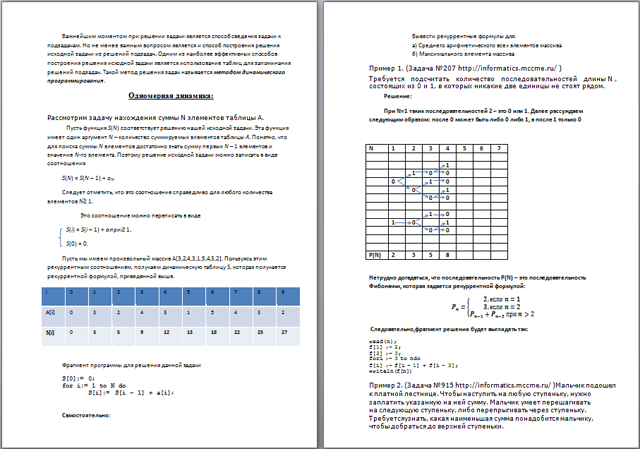
Важнейшим моментом при решении задачи является способ сведения задачи к подзадачам. Но не менее важным вопросом является и способ построения решения исходной задачи из решений подзадач. Одним из наиболее эффективных способов построения решения исходной задачи является использование таблиц для запоминания решений подзадач. Такой метод решения задач называется методом динамического программирования.
Одномерная динамика:
Рассмотрим задачу нахождения суммы N элементов таблицы A.
Пусть функция S(N) соответствует решению нашей исходной задачи. Эта функция имеет один аргумент N – количество суммируемых элементов таблицы A. Понятно, что для поиска суммы N элементов достаточно знать сумму первых N – 1 элементов и значение N-го элемента. Поэтому решение исходной задачи можно записать в виде соотношения
S(N) = S(N – 1) + aN.
Следует отметить, что это соотношение справедливо для любого количества элементов N 1.
Это соотношение можно переписать в виде
 S(i) = S(i – 1) + ai при i≥ 1,
S(i) = S(i – 1) + ai при i≥ 1,
S(0) = 0.
Пусть мы имеем произвольный массив A[3,2,4,3,1,5,4,3,2]. Пользуясь этим рекуррентным соотношением, получаем динамическую таблицу S, которая получается рекуррентной формулой, приведенной выше.
| i | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|
|
| A[i] | 0 | 3 | 2 | 4 | 3 | 1 | 5 | 4 | 3 | 2 |
| S[i] | 0 | 3 | 5 | 9 | 12 | 13 | 18 | 22 | 25 | 27 |
Фрагмент программы для решения данной задачи
S[0]:= 0;
for i:= 1 to N do
S[i]:= S[i – 1] + a[i];
Самостоятельно:
Вывести рекуррентные формулы для:
а) Среднего арифметического всех элементов массива
б) Максимального элемента массива
Пример 1. (Задача №207 http://informatics.mccme.ru/ )
Требуется подсчитать количество последовательностей длины N , состоящих из 0 и 1, в которых никакие две единицы не стоят рядом.
Решение:
При N=1 таких последовательностей 2 – это 0 или 1. Далее рассуждаем следующим образом: после 0 может быть либо 0 либо 1, а после 1 только 0
| N | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|
|
|
|
|
|
|
|
|
|
|
|
| 
| 1 |
|
|
|
|
| 
| 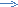 1 1
|  0 0
| 0 |
|
|
|
|
|  0 0
| 
|  1 1
| 0 |
|
|
|
|
|
|  0 0
| 
| 1 |
|
|
|
|
|
|
|  0 0
| 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 
|  1 1
| 0 |
|
|
|
|
|  1 1
|  0 0
| 
| 1 |
|
|
|
|
|
|
|  0 0
| 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| P(N) | 2 | 3 | 5 | 8 |
|
|
|
Нетрудно догадаться, что последовательность P(N) – это последовательность Фибоначчи, которая задается рекуррентной формулой:
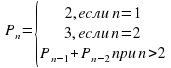
Следовательно, фрагмент решения будет выглядеть так:
read(n);
f[1] := 2;
f[2] := 3;
for i := 3 to n do
f[i] := f[i - 1] + f[i - 2];
writeln(f[n])
Пример 2. (Задача №915 http://informatics.mccme.ru/ ) Мальчик подошел к платной лестнице. Чтобы наступить на любую ступеньку, нужно заплатить указанную на ней сумму. Мальчик умеет перешагивать на следующую ступеньку, либо перепрыгивать через ступеньку. Требуется узнать, какая наименьшая сумма понадобится мальчику, чтобы добраться до верхней ступеньки.
Входные данные
В первой строке входного файла вводится одно натуральное число N 100 — количество ступенек.
100 — количество ступенек.
В следующей строке вводятся N натуральных чисел, не превосходящих 100 — стоимость каждой ступеньки (снизу вверх).
Выходные данные
Выведите одно число — наименьшую возможную стоимость прохода по лесенке.
Решение:
Допустим, что мы находимся на последней ступеньке и его стоимость an. Мы можем подняться на эту ступеньку, либо с предыдущей, либо с пред предыдущей. Выгодней будет с той которая меньше стоит. Поэтому решение будет таким:
readln(n);
for i:=1 to n do read(a[i]);
p[1]:=a[1];
p[2]:=a[2];
for i:=3 to n do p[i]:=MIN(p[i-1],p[i-2])+a[i];
writeln(p[n])
Пример 3.(Задача №2963 http://informatics.mccme.ru/ )
Имеется калькулятор, который выполняет три операции:
Прибавить к числу X единицу.
Умножить число X на 2.
Умножить число X на 3.
Определите, какое наименьшее число операций необходимо для того, чтобы получить из числа 1 заданное число N.
Входные данные
Программа получает на вход одно число, не превосходящее 106.
Выходные данные
Требуется вывести одно число: наименьшее количество искомых операций.
Решение на Python:
n=int(input())
p=[0]*(n+1)
for i in range(2,n+1):
if i%2==0 and i%3!=0:
p[i]=min(p[i//2],p[i-1])+1
elif i%3==0 and i%2!=0:
p[i]=min(p[i//3],p[i-1])+1
elif i%3==0 and i%2==0:
p[i]=min(p[i//3],p[i//2],p[i-1])+1
else:
p[i]=p[i-1]+1
print(p[n])
Двумерная динамика на таблицах:
Пример 4. (Задача №206 http://informatics.mccme.ru/ ) В прямоугольной таблице NxM в начале игрок находится в левой верхней клетке. За один ход ему разрешается перемещаться в соседнюю клетку либо вправо, либо вниз (влево и вверх перемещаться запрещено). Посчитайте, сколько есть способов у игрока попасть в правую нижнюю клетку.
Входные данные
Вводятся два числа N и M - размеры таблицы (1NM
Выходные данные
Выведите искомое количество способов.
Пример 5. Дан лист клетчатой бумаги. Часть клеток закрашены чёрным цветном. Требуется найти, сколько существует способов вырезать из этого листа квадрат, состоящий только из незакрашенных клеток.
Формат входных данных
В первой строке через пробел записаны целые числа r и c (1 ≤ r, c ≤5000) — количество строк и столбцов на листе. Во второй строке находится количество закрашенных клеток n (0 ≤ n ≤ 100000). Гарантируется также, что (n ≤ r c). В следующих n строках записаны координаты чёрных клеток. Каждая закрашенная клетка задаётся номером строки i (1 ≤ i ≤r) и номером столбца j (1 ≤ j ≤ c), в которых она находится.
Формат результата
Выведите искомое количество способов.
Решение на Python:
r,c=map(int,input().split())
a=[]
for i in range(r):
a.append(c*[1])
n=int(input())
for i in range(0,n):
x,y=map(int,input().split())
a[x-1][y-1]=0
for i in range(1,r):
for j in range(1,c):
if a[i-1][j-1]!=0 and a[i][j-1]!=0 and a[i-1][j]!=0 :
a[i][j]=min(a[i-1][j-1],a[i][j-1],a[i-1][j])+1
s=0
for i in range(r):
s=s+sum(a[i])
print(s)

 Получите свидетельство
Получите свидетельство Вход
Вход


 S(i) = S(i – 1) + ai при i≥ 1,
S(i) = S(i – 1) + ai при i≥ 1,

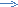 1
1 0
0 0
0
 0
0

 1
1 0
0
 0
0










 Метод динамического программирования (методическая разработка) (62.49 КB)
Метод динамического программирования (методическая разработка) (62.49 КB)
 0
0 1617
1617 125
125 Нравится
0
Нравится
0








