Получите свидетельство
Вход
| РАССМОТРЕНО : на заседании ПЦК№1
| ЭКЗАМЕН По дисциплине ОУД 04 «Математика» Для профессии 15.01.05 Сварщик (ручной и частично механизированной сварки (наплавки) | УТВЕРЖДАЮ: | ||||||||
| Вид | ||||||||||
| В результате освоения учебной дисциплины обучающийся должен уметь: решать рациональные, показательные, логарифмические, тригонометрические уравнения, сводящиеся к линейным и квадратным, а также аналогичные неравенства и системы; находить производные и первообразные элементарных функций; вычислять в простейших случаях площади и объемы с использованием определенного интеграла; использовать производную для изучения свойств функций и построения графиков; решать планиметрические и простейшие стереометрические задачи на нахождение геометрических величин (длин, углов, площадей, объемов); проводить доказательные рассуждения в ходе решения задач; описывать взаимное расположение прямых и плоскостей в пространстве. находить значения корня, степени, логарифма, тригонометрических функций; выполнять преобразования выражений, применяя формулы, связанные со свойствами степеней, логарифмов, тригонометрических функций; определять основные свойства числовых функций, строить графики функций, иллюстрировать по графику свойства элементарных функций; изображать основные многогранники и круглые тела; выполнять чертежи по условиям задач; находить вероятности событий и элементы комбинаторики В результате освоения учебной дисциплины обучающийся должен знать: теоретические основы начал математического анализа формулировки аксиом и основных теорем и их следствий стереометрии и планиметрии; понятия тела вращения: цилиндр, конус и шар; свойств перпендикуляра и наклонной; понятия объема тел и площадей поверхностей; понятия о числовых функциях и их основных свойствах, графиках функций. свойства и графики степенной, показательной, логарифмической и тригонометрических функций; свойства иррациональных. показательных, логарифмических, тригонометрических уравнений и неравенств; приемы решения уравнений и неравенств с одной и двумя переменными; обобщенное понятие о степени числа, корня n-степени из числа логарифм числа; основы комбинаторики и теории вероятностей В процессе освоения учебной дисциплины у студентов должны быть формировать общие компетенции: ОК1.Понимать сущность и социальную значимость своей будущей профессии, проявлять к ней устойчивый интерес. ОК2.Организовывать собственную деятельность, исходя из цели и способов ее достижения, определенных руководителем OK3.Анализировать рабочую ситуацию, осуществлять текущий и итоговый контроль, оценку и коррекцию собственной деятельности, нести ответственность за результаты своей работы. OK4.Осуществлять поиск информации, необходимой для эффективного выполнения профессиональных задач. OK5.Использовать информационно-коммуникационные технологии в профессиональной деятельности. ОК6.Работать в команде, эффективно общаться с коллегами, руководством ОК 7. Брать на себя ответственность за работу членов команды (подчиненных), результат выполнения заданий. ОК 8. Самостоятельно определять задачи профессионального и личностного развития, заниматься самообразованием, осознанно планировать повышение квалификации. ОК 9. Ориентироваться в условиях частой смены технологий в профессиональной деятельности. Формой аттестации по учебной дисциплине ОУД.04 Математика является письменный экзамен.
| ||||||||||
| Инструкция Для проведения промежуточной аттестации в виде экзамена по дисциплине ОУД.04 Математика предлагаются задания в 4-х вариантах . Письменная экзаменационная работа по учебной дисциплине ОУД, 04 Математика состоит из 2-х частей: обязательной и дополнительной. В обязательную часть включаются задания минимально обязательного уровня, в дополнительную часть – более сложные. В обязательную часть работы включены задания базового уровня по всем основным разделам требований ФГОС – геометрия (планиметрия и стереометрия), алгебра, начала математического анализа, теория вероятностей, комбинаторика. При выполнении заданий обязательной части обучающиеся должны продемонстрировать базовую математическую компетентность. Задания этой группы проверяют базовые вычислительные и логические умения и навыки, умение анализировать информацию, представленную в графиках и таблицах, использовать простейшие вероятностные и статистические модели, ориентироваться в простейших геометрических конструкциях, владение основными алгоритмами, знание и понимание ключевых элементов содержания (математических понятий, их свойств, приемов решения задач и пр.), умение пользоваться математической записью, а также применять математические знания в простейших практических ситуациях. Обязательная часть содержит 14 заданий. Каждое задание первой части (В1 – В14) оценивается в 1 балл. Дополнительная часть направлена на проверку владения материалом на повышенном уровне и умение решать математические задачи, не сводящиеся к прямому применению алгоритма. Эта часть содержит 8 заданий повышенного уровня сложности из различных разделов курса математики. Каждое задание второй части (С1 – С8) оценивается в 2 балла. В назначенный день для проведения экзамена студенты получают задания. Максимальный балл за выполнение всей работы – 30 баллов. | ||||||||||
| Критерии
| ||||||||||
Вариант 1
| При выполнении заданий В1–В15 запишите сначала номер задания, а затем его подробное решение и полученный ответ. |
В1 Поезд отправился из Санкт-Петербурга в 23 часа 50 минут (время московское) и прибыл в Москву в 7 часов 50 минут следующих суток. Сколько часов поезд находился в пути?
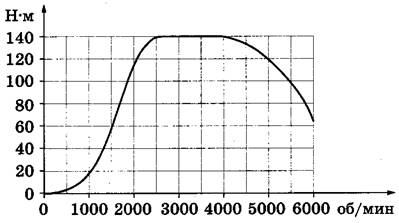
В2 На графике изображена зависимость крутящего момента двигателя от числа его оборотов в минуту. На оси абсцисс откладывается число оборотов в минуту, на оси ординат — крутящий момент в Н∙м. Какое число оборотов в минуту должен совершать двигатель, чтобы крутящий момент был не менее 60 Н∙м?
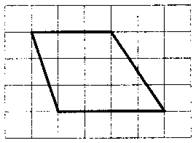
В3 На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите длину средней линии этой трапеции.
В4 Строительный подрядчик планирует купить 5 тонн облицовочного кирпича у одной из трех поставщиков. Один кирпич весит 5 кг. Цена кирпича и условия доставки представлены в таблице. Во сколько рублей обойдется наиболее дешевый вариант покупки с доставкой
| Поставщик | Цена кирпича (руб. за штуку) | Стоимость доставки | Дополнительные условия |
| А | 17 | 7000 | Нет |
| Б | 18 | 6000 | Доставка бесплатна, если сумма заказа превышает 50000руб. |
| В | 19 | 4500 | Доставка со скидкой 50%, если сумма заказа превышает 60000руб |
В5 В фирме такси в наличии 60 легковых автомобилей; 27 из них чёрного цвета с жёлтыми надписями на боках, остальные — жёлтого цвета с чёрными надписями. Найдите вероятность того, что на случайный вызов приедет машина жёлтого цвета с чёрными надписями.
В6 Найдите корень уравнения
В7 Найдите корень уравнения log2 (2x+1) = log2 3
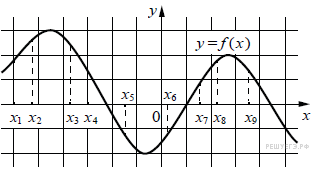
В8. На рисунке изображён график дифференцируемой функции y = f(x). На оси абсцисс отмечены девять точек: x1, x2, …, x9. Среди этих точек найдите все точки, в которых производная функции y = f(x) отрицательна. В ответе укажите количество найденных точек.
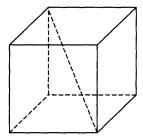
В9 Диагональ куба равна
. Найдите его объём.
В10. Установите соответствие между величинами и их возможными значениями: к каждому элементу первого столбца подберите соответствующий элемент из второго столбца.
| ВЕЛИЧИНЫ | ВОЗМОЖНЫЕ ЗНАЧЕНИЯ |
| А рост ребенка | 1) 32 км |
| Б толщина листа бумаги | 2) 30 м |
| В протяженность автобусного маршрута | 3) 0,2 мм |
| Г высота жилого дома | 4) 110 см |
| А | Б | В | Г |
| | | | |
В таблице под каждой буквой, соответствующей величине, укажите номер её возможного значения.
В11. Найдите значение выражения 91,5 – 810,5 – (0,5)-2.
В12 Радиус основания цилиндра равен 4 см, площадь боковой поверхности вдвое больше площади основания. Найти объем цилиндра.
В13 Колесо имеет 6 спиц. Найдите величину угла (в градусах), который образован соседними спицами.
В 14 Установите соответствие (ответы даны в именительном падеже)
| 1.Функция, заданная формулой вида y= ax называется … | а) апофема; б) определения; в) значений; г) биссектриса; д) показательная; е) дифференцирование ж) логарифмическая; з) интегрирование |
| 2. Высота боковой грани правильной пирамиды называется… | |
| 3. Нахождение всех первообразных функции называется … | |
| 4. Все значения независимой переменной образуют область … функции |
Часть 2
| При выполнении заданий С1–С5 запишите сначала номер задания, а затем его подробное решение и полученный ответ. |
С1 Решите уравнение 
и найдите корни, принадлежащие отрезку 
С2 Вычислите: 
С3 Найдите площадь плоской фигуры (сделав чертеж), ограниченной линиями
.
С4 Решите уравнение: 
С5 Решите систему уравнений: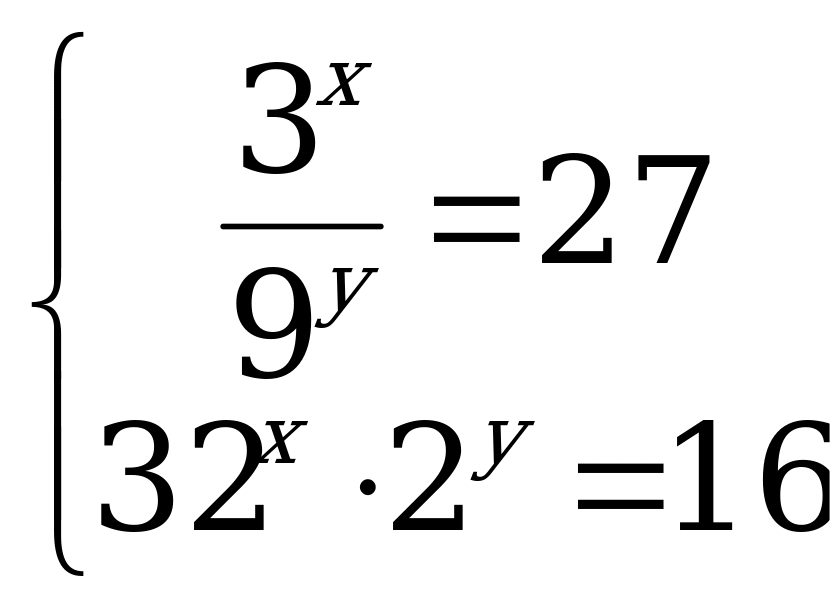 
С6 Сварщику необходимо изготовить бункер, имеющий форму правильной четырехугольной призмы, длина стороны основания которого равна 1,2 м, высота – 2,4 м. Сколько стали необходимо выполнения работы? (Прим.: на швы следует добавить 3% материала).
С 7 Найдите наибольшее значение функции 
на отрезке [-3; 1].
С8 Основание прямой призмы – равнобочная трапеция, одно из оснований которой в два раза больше другого. Непараллельные боковые грани призмы – квадраты. Высота призмы равна 6 см. Площадь боковой поверхности призмы равна 144 см2. Вычислите объем призмы.
Вариант 2
При выполнении заданий В1–В15 запишите сначала номер задания, а затем его подробное решение и полученный ответ.
В1. Держатели дисконтной карты книжного магазина получают при покупке скидку 6%. Книга стоит 650 рублей. Сколько рублей заплатит держатель дисконтной карты за эту книгу?
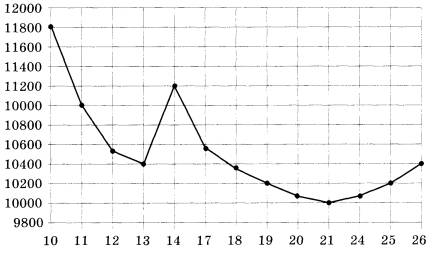
В2. На рисунке жирными точками показана цена никеля на момент закрытия биржевых торгов во все рабочие дни с 10 по 26 ноября 2008 года. По горизонтали указываются числа месяца, по вертикали — цена тонны никеля в долларах США. Для наглядности жирные точки на рисунке соединены линией. Определите по рисунку разность между наибольшей и наименьшей ценой никеля на момент закрытия торгов в указанный период (в долларах США за тонну)
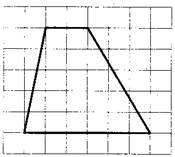
В3 На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите длину средней линии этой трапеции.
В4 Строительная фирма планирует купить 70 м3пеноблоков у одного из трёх поставщиков. Цены и условия доставки приведены в таблице.
| Поставщик | Стоимость пеноблоков (руб. за 1м3) | Стоимость доставки (руб.) | Дополнительные условия |
| А | 2600 | 10 000 | Нет |
| Б | 2800 | 8000 | При заказе товара на сумму свыше 150 000 рублей доставка бесплатная |
| В | 2700 | 8000 | При заказе товара на сумму свыше 200 000 рублей доставка бесплатная |
Сколько рублей нужно заплатить за самую дешёвую покупку с доставкой?
В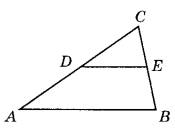
5. На клавиатуре телефона 10 цифр, от 0 до 9. Какова вероятность того, что случайно нажатая цифра будет чётной и больше 3?
В6 Найдите корень уравнения: 
В7 Площадь треугольника ABC равна 152. DE — средняя линия. Найдите площадь треугольника CDE.
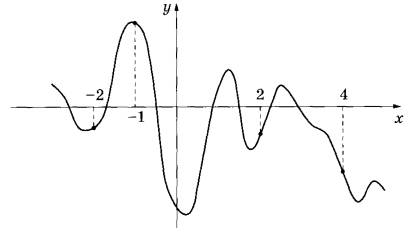
В8 На рисунке изображён график функции у = f(x). На оси абсцисс отмечены точки -2, -1, 2, 4. В какой из этих точек значение производной наибольшее? В ответе укажите эту точку.
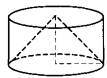
В9 Цилиндр и конус имеют общие основание и высоту. Объём конуса равен 28. Найдите объём цилиндра.
В10. Установите соответствие между величинами и их возможными значениями: к каждому элементу первого столбца подберите соответствующий элемент из второго столбца.
| ВЕЛИЧИНЫ | ВОЗМОЖНЫЕ ЗНАЧЕНИЯ |
| А Скорость движения велосипедиста | 1) 0,4м/мин |
| Б Скорость полета космического корабля | 2) 15км/ч |
| В Скорость распространения света | 3) 20000 км/ч |
| Г Скорость движения улитки | 4) 300 000 км/с |
| А | Б | В | Г |
| | | | |
В таблице под каждой буквой, соответствующей величине, укажите номер её возможного значения.
В11 Найдите значение выражения
.
В12 В розетку электросети подключены приборы, общее сопротивление которых составляет R1=56 Ом. Параллельно с ними в розетку предполагается подключить электрообогреватель. Определите наименьшее возможное сопротивление R2 этого электрообогревателя, если известно, что при параллельном соединении двух проводников с сопротивлениями R1 и R2 их общее сопротивление задаётся формулой
, а для нормального функционирования электросети общее сопротивление в ней должно быть не меньше 24 Ом. Ответ дайте в омах.
В13. Человеку ростом 180 см нужно поменять лампочку, расположенную на стене дома на высоте 420 см. Для этого у него есть лестница длиной 3 метра. На каком наибольшем расстоянии от стены должен быть установлен нижний конец лестницы, чтобы с последней ступеньке человек дотянулся до лампочки? Ответ запишите в метрах
В14 Установите соответствие (ответы даны в именительном падеже)
| 1.Функция, заданная формулой вида y= logax называется … | а) основание; б) определения; в) значений; г) показатель; д) показательная; е) дифференцирование ж) логарифмическая; з) интегрирование |
| 2. Логарифмом числа b по основанию, а называется… степени, в которую нужно возвести, а, чтобы получить b | |
| 3. Нахождение производной функции называется … | |
| 4. Все значения зависимой переменной образуют область … функции |
Часть 2
| При выполнении заданий С1–С5 запишите сначала номер задания, а затем его подробное решение и полученный ответ. |
С1 Решите уравнение
и найдите корни, принадлежащие отрезку 
C2. Вычислите: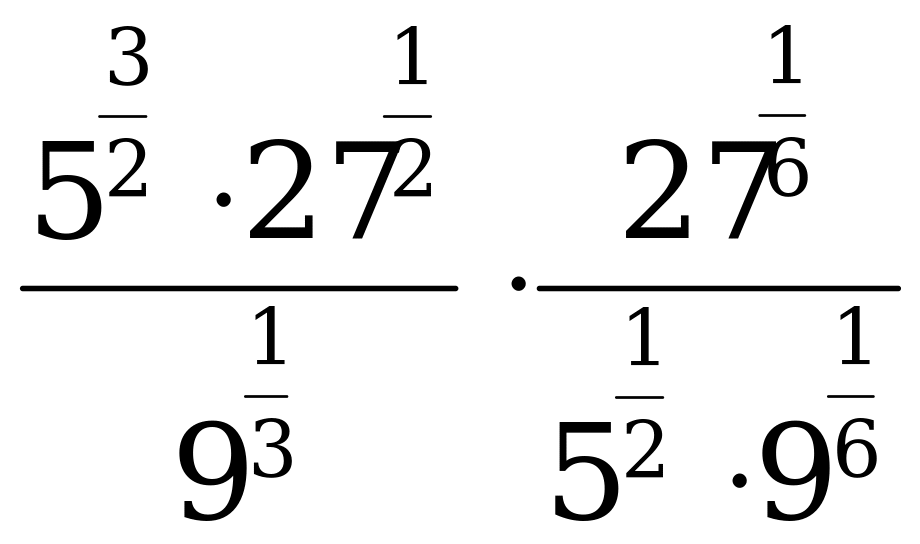 
С3 Найти площадь фигуры (сделав чертеж), ограниченной осями координат, графиком функции y=x2 - 6x + 8 и прямой y = 3.
С4 Решите уравнение: 
С5 Решите систему: 
С6 Сварщику необходимо узнать, сколько кубических метров шлака вместится в контейнер, имеющий форму усеченной пирамиды, длина сторон основания которой 1,2 м и 2,4 м, а высота – 2м.
С 7 Найдите наибольшее значение функции. 
на отрезке [0;8]
С 8 Площадь боковой поверхности конуса равна 20 π см2, а площадь его основания на 4 π см2 меньше. Вычислите объем конуса.
Вариант 3
| При выполнении заданий В1 – В15 запишите сначала номер задания, рядом краткое решение и ответ |
Часть1
В1. Джинсы до распродажи стоили 1500 рублей. Катя купила джинсы во время распродажи со скидкой 20%. Сколько рублей Катя заплатила за джинсы?
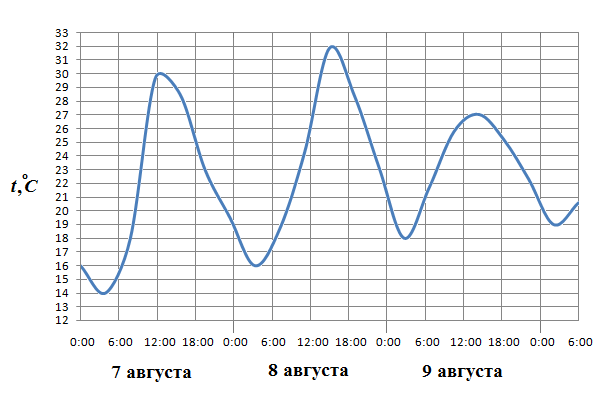
В2 . На рисунке показано изменение температуры воздуха на протяжении трех суток. По горизонтали указывается дата и время суток, по вертикали — значение температуры в градусах Цельсия. Определите по рисунку наименьшую температуру воздуха 9 августа.
В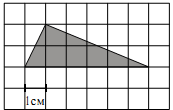
3. На клетчатой бумаге с размером клетки 1 см × 1 см изображён треугольник. Найдите его площадь. Ответ дайте в см2
В 4. Для транспортировки 5 тонн груза на 150 км можно воспользоваться услугами одной из трех фирм-перевозчиков. Стоимость перевозки и грузоподъемность автомобилей для каждого перевозчика указана в таблице. Сколько рублей придется заплатить за самую дешевую перевозку?
| Перевозчик | Стоимость перевозки одним автомобилем (руб. на 10 км) | Грузоподъемность автомобилей (тонн) |
| A | 90 | 1.8 |
| Б | 120 | 2.4 |
| В | 180 | 3,6 |
В5. На мероприятие было закуплено 13 синих,11красных, 6 жёлтых и 20 белых футболок. Какова вероятность того, что Саше достанется красная футболка?
В6. Найдите корень уравнения
.
В7. Углы треугольника относятся как 4:6:5. Найдите меньший из них. Ответ дайте в градусах.
В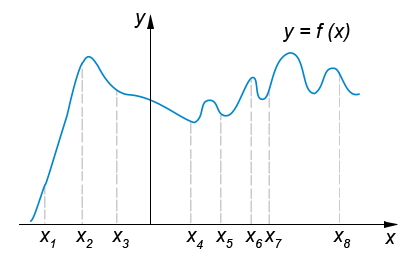 
8 (1балл). На рисунке изображён график функции y=f(x) и восемь точек на оси абсцисс: x1, x2, x3, x4,x5, x6, x7, x8. В скольких из этих точек производная функции f(x) отрицательна?
В9. Конус имеет высоту, равную 16 см, и образующую, равную 20 см. Найдите объём конуса (в см3), в ответе укажите объем, делённый на π, т.е. 
В10. Установите соответствие между величинами и их возможными значениями: к каждому элементу первого столбца подберите соответствующий элемент из второго столбца.
| ВЕЛИЧИНЫ | ВОЗМОЖНЫЕ ЗНАЧЕНИЯ |
| А) масса взрослого кита Б) объём железнодорожного вагона В) площадь волейбольной площадки Г) ширина футбольного поля | 1) 162 кв. м 2) 100 т 3) 120 м3 4) 68 м |
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
| А | Б | В | Г |
|
|
|
|
|
В11.Найдите значение выражения 
В12. Локатор батискафа, равномерно погружающегося вертикально вниз, испускает ультразвуковой сигнал частотой 749 МГц. Приёмник регистрирует частоту сигнала, отражённого от дна океана. Скорость погружения батискафа (в м/с) и
частоты связаны соотношением:
, где c =1500 м/с — скорость звука в воде; f0 — частота испускаемого сигнала (в МГц), f — частота отражённого сигнала (в МГц). Найдите частоту отражённого сигнала (в МГц), если батискаф погружается со скоростью 2 м/с.
В13. Какой наименьший угол (в градусах) образуют минутная и часовая стрелки часов в 16:00?
| 1.Функция f(x) называется …, если для любого x из области определения f(-x) =-f(x); | а) четная; б) определения; в) значений; г) синусоида; д) парабола; е) дифференцируемая ж) нечетная; з) интегрируемая |
| 2. Функция, имеющая производную в точке х0 называется…? | |
| 3. График функции y=sin x называется…? | |
| 4. Все значения независимой переменной образуют область … функции |
В14. Установите соответствие (ответы даны в именительном падеже)
Часть 2
| При выполнении заданий С1–С5 запишите сначала номер задания, а затем его подробное решение и полученный ответ. |
С1 Решите уравнение и найдите корни, принадлежащие отрезку
С2 Вычислите:
С3 Найдите площадь плоской фигуры (сделав чертеж), ограниченной линиями .
С4 Решите уравнение:
С5 Решите систему уравнений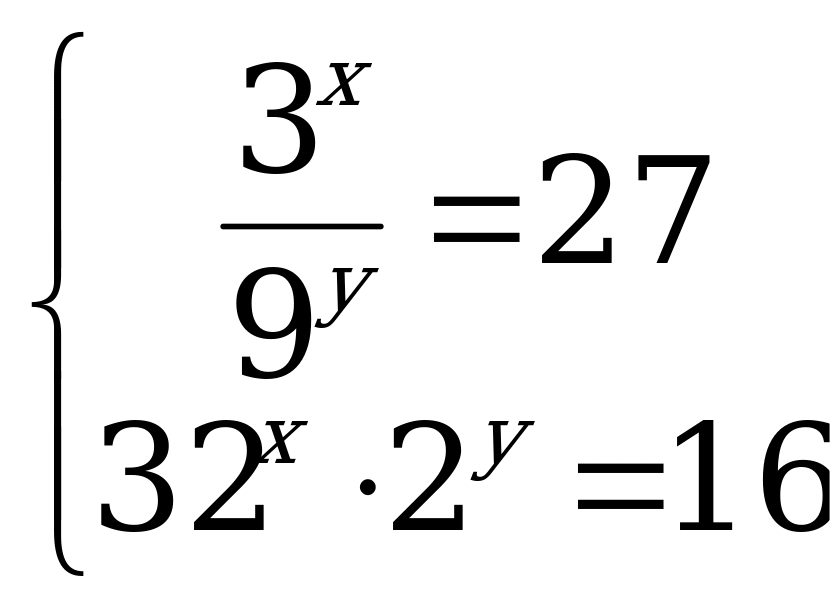
С6 Необходимо изготовить воронку, представляющую форму усеченного конуса. Радиусы оснований: 2 м и 10 м, высота – 30 м. Сколько потребуется металла на изготовление такой воронки, если на сварку добавить 3% материала?
С 7 Найдите точку минимума функции: 
С 8 В правильной четырехугольной пирамиде сторона основания равна 10 см, а боковое ребро – 13 см. Найти высоту пирамиды.
Вариант 4
| При выполнении заданий В1 – В15 запишите сначала номер задания, рядом краткое решение и ответ |
В1. В общежитии техникума в каждой комнате можно поселить четырех человек. Какое наименьшее количество комнат необходимо для поселения 89 иногородних студентов?
В 2. На рисунке жирными точками показан курс евро, установленный Центробанком РФ, во все рабочие дни с 1 февраля по 28 февраля 2003 года. По горизонтали указываются числа месяца, по вертикали — цена евро в рублях. Для наглядности жирные точки на рисунке соединены линией. Определите по рисунку, какой был курс евро 15 февраля. Ответ дайте в рублях.
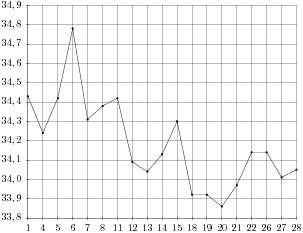
В 3. На клетчатой бумаге с клетками размером 1 см 
1 см изображен треугольник (см. рисунок). Найдите его площадь в квадратных сантиметрах.
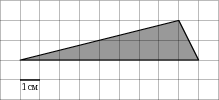
В 4. При строительстве сельского дома можно использовать один из двух типов фундамента: каменный или бетонный. Для каменного фундамента необходимо 10 тонн природного камня и 9 мешков цемента. Для бетонного фундамента необходимо 7 тонн щебня и 50 мешков цемента. Тонна камня стоит 1500 рублей, щебень стоит 680 рублей за тонну, а мешок цемента стоит 250 рублей. Сколько рублей будет стоить материал для фундамента, если выбрать наиболее дешевый вариант?
В 5. В соревнованиях по толканию ядра участвуют 5 спортсменов из Македонии, 3 спортсмена из Сербии, 3 спортсмена из Хорватии и 9 — из Словении. Порядок, в котором выступают спортсмены, определяется жребием. Найдите вероятность того, что спортсмен, который выступает последним, окажется из Словении.
В 6. Найдите корень уравнения: 
.
В 7. Найдите значение выражения: (7x-5)(7x+5)-49x2+7x-37 при x=140
В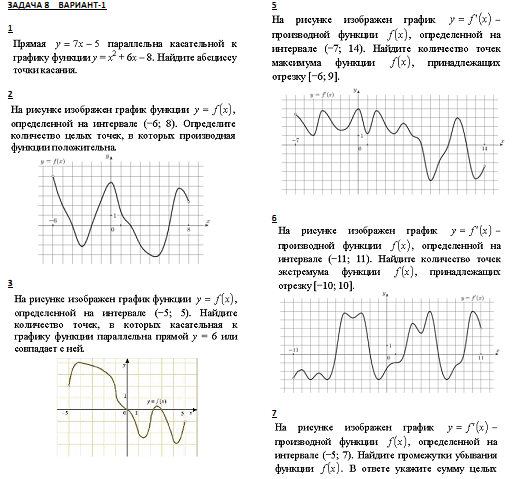
8. На рисунке изображен график функции производной 
функции y=f(x), определенной на интервале (-7;14). Найдите количество точек максимума функции y=f(x), принадлежащих отрезку [-6;9]
В9. В первом цилиндрическом сосуде уровень жидкости достигает 16 см. Эту жидкость перелили во второй цилиндрический сосуд, диаметр основания которого в 2 раза больше диаметра основания первого. На какой высоте будет находиться уровень жидкости во втором сосуде? Ответ выразите в см.
В10. Установите соответствие между величинами и их возможными значениями:
| ВЕЛИЧИНЫ | ВОЗМОЖНЫЕ ЗНАЧЕНИЯ |
| А) скорость движения автомобиля Б) скорость движения пешехода В) скорость движения улитки Г) скорость звука в воздушной среде | 1) 0,5 м/мин 2) 60 км/час 3) 330 м/сек 4) 4 км/час |
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
| А | Б | В | Г |
|
|
|
|
|
В11. Найдите значение выражения 
.
В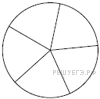
12. В розетку электросети подключены приборы, общее сопротивление которых составляет R1=110 Ом. Параллельно с ними в розетку предполагается подключить электрообогреватель. Определите наименьшее возможное сопротивление R2 этого электрообогревателя, если известно, что при параллельном соединении двух проводников с сопротивлениями R1 Ом и R2 Ом их общее сопротивление выражается формулой
(Ом), а для нормального функционирования электросети общее сопротивление в ней должно быть не меньше 10Ом. Ответ выразите в омах
В13 Колесо имеет 5 спиц. Найдите величину угла (в градусах), который образуют две соседние спицы.
В14. Установите соответствие (ответы даны в именительном падеже)
| 1. Точки максимума и минимума функции называют …?; | а) нечетная; б) показатель; в) экстремум; г) синусоида; д) прямая; е) дифференцирование; ж) гипербола; з) производной f(х0). |
| 2. Разностное отношение приращения функции в точке х0 к приращению аргумента | |
| 3. График функции 4. Логарифмом числа b по основанию a называют … степени в которую надо возвести, а чтобы получить b |
. если
называется…?
называется…?;
Часть 2
| При выполнении заданий С1–С6 запишите сначала номер задания, а затем его подробное решение и полученный ответ. Единицы измерений писать не нужно. |
С1 Решите уравнение 
и найдите корни, принадлежащие отрезку 
С2 Вычислите: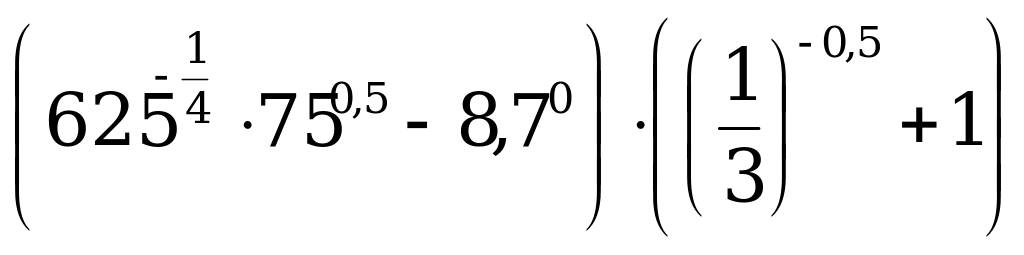 
С3 Найти площадь плоской фигуры (сделав чертеж), ограниченной линиями 
.
С4 Решите уравнение: 
С5 Решите систему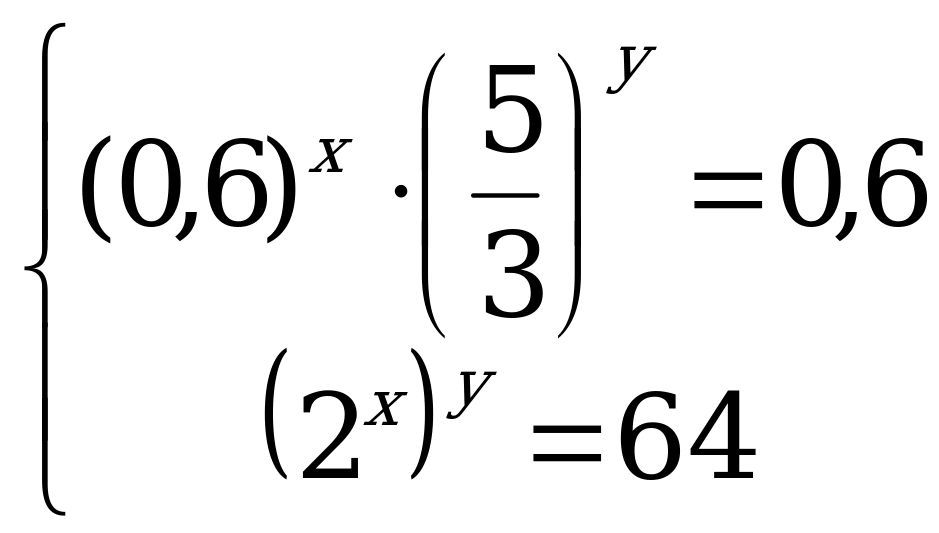
С6 Сварщику необходимо изготовить бункер, имеющий форму правильной четырехугольной призмы, длина стороны основания которого равна 1,2 м, высота – 2,4 м. Сколько стали необходимо выполнения работы? (Прим.: на швы следует добавить 3% материала).
С 7 .Найдите наименьшее значение функции: 
на отрезке[-2;0]
С 8 Площадь осевого сечения цилиндра равна 108 см2, а его образующая в три раза меньше диаметра основания. Найдите площадь полной поверхности цилиндра.
Эталон выполнения заданий
Ответы к заданиям с выбором ответа и кратким ответом
| № задания | Вариант 1 | Вариант 2 | Вариант 3 | Вариант 4 |
| В1 | 8 | 611 | 1200 | 23 |
| В2 | 1500 | 1800 | 18 | 34,3 |
| В3 | 3,5 | 4 | 6 | 9 |
| В4 | 23500 | 192000 | 4050 | 17250 |
| В5 | 0,55 | 0,3 | 0,22 | 0,45 |
| В6 | 5 | -18 | 8 | -12 |
| В7 | 1 | 38 | 48 | 918 |
| В8 | 4 | 2 | 5 | 4 |
| В9 | 64 | 84 | 768 | 4 |
| В10 | 4312 | 2341 | 2314 | 2413 |
| В11 | 14 | 5 | 20 | 5 |
| В12 | 64π см3 | 42 | 751 | 11 |
| В13 | 600 | 1,8 | 48 | 72 |
| В14 | дазб | жгев | жегб | вздб |
| № задания | С1 | С2 | С3 | С4 | С5 | С6 | С7 | С8 |
| Вариант 1 |
| -6 | 4,5 | 63 | (1;-1) | 13,35 | 48 | 144 √2 |
| Вариант 2 |
| 15 |
|
| (7;1) | 6,72 | 19 | 16 π см3 |
| Вариант 3 |
| -6 | 4,5 | 63 | (1;-1) | 1205,06 | 0 | √ 119 см |
| Вариант4 |
| 2 |
| 6,0625 | (-2;-3); (3;2) | 13,35 | -4 | 270 π см2 |
Материалы к экзамену по математике для СПО (532 KB)
0
217
4
Нравится
0
