Пояснительная записка
Промежуточная аттестация по математике (алгебра и начала математического анализа, и геометрия) в 10 классах проводится в форме теста, состоящего из двух частей (модели экзаменационной работы по математике в 11 классах).
Тест составлен с использованием заданий из открытого банка тестовых заданий единого государственного экзамена (ЕГЭ) за курс математики средней (полной) общей школы с учетом программного материала, изученного десятиклассниками за текущий учебный год.
Назначение экзаменационной работы: оценить уровень предметных компетенций учащихся 10 классов по математике (алгебра и начала математического анализа).
Время выполнения экзаменационной работы:
На выполнение итоговой контрольной работы отводится 60 минут (1 час).
Условия проведения экзаменационной работы и проверки работ, требованиям к специалистам
Учащимся в начале экзамена выдается полный текст работы. Ответы на задания первой части могут фиксироваться непосредственно в тексте работы. Все необходимые вычисления, преобразования и чертежи учащиеся могут производить в черновике. Черновики не проверяются.
Проверку экзаменационной работы осуществляет учитель математики.
Система оценивания выполнения отдельных заданий и экзаменационной работы в целом
За выполнение каждого задания ученик получает определенное число баллов. Правильно выполненная вся работа оценивается 25 баллами. В таблице 1 приводится система формирования общего балла.
Таблица 1.
| Часть 1 | Часть 2 | ||
| 1- 15 | 16, 17 | 18, 19 | № 1-19 |
| 1 | 2 | 3 | 25 |
В случае правильного выполнения задания части 1(1-15) учащемуся засчитывается 1 балл, если ответ неверный или отсутствует – 0 баллов. Задание части 1 считается выполненным правильно, если вписан верный ответ.
Задание части 2 (16-19) считается выполненным правильно, если учащийся выбрал правильный путь решения, из письменной записи решения понятен ход его рассуждений, получен верный ответ. В этом случае ему выставляется полный балл (2 ,3), соответствующий данному заданию. При выполнении заданий части 2 можно использовать без доказательства и ссылок любые математические факты, содержащиеся в учебниках и учебных пособиях, входящих в Федеральный перечень учебников, рекомендованных (допущенных) Министерством образования и науки Российской Федерации.
С учетом числа заданий базового уровня, разработана шкала перевода первичных баллов в отметки по пятибалльной системе (таблица 2)
Таблица 2.
Таблица перевода суммарного балла в 5-балльную шкалу
| Отметка по 5-балльной шкале | «2» | «3» | «4» | «5» |
| Первичный балл | 0-4 баллов | 5-14 баллов | 15-19 баллов | 20-25 баллов |
Вариант №1
Часть I.
1. Вычислить 
2. Найти производную функции 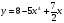 при х= -1
при х= -1
3. Решить уравнение 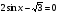
4. Вычислить, используя формулы приведения 
5. Найти производную функции 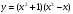 при х=2
при х=2
6. Вычислить 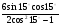
7. Найдите значение производной функции 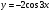 в точке
в точке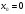
8. Найдите значение производной функции 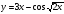 в точке
в точке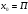
9. Упростите 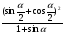
10. Вычислить  , если
, если 
11. Найдите угловой коэффициент касательной  в точке
в точке
12. Решить уравнение  . В ответе укажите наименьший положительный корень уравнения.
. В ответе укажите наименьший положительный корень уравнения.
13. Упростите 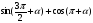 при а=0
при а=0
14. Найдите значение производной функции  в точке
в точке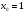
15. Найти производную функции 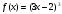
Часть II.
16. Сколько корней имеет уравнение (cos x*cos 3x + sin x*sin ( П-3x))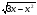 =0
=0
17. Найдите значение выражения 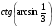 .
.
18 . Решите задачу: Апофема правильной четырехугольной пирамиды равна 4см, а двугранный угол при основании равен 60°. Найдите полную поверхность пирамиды.
19. Составьте уравнение касательной к графику функции 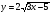 в точке с абсциссой x=2
в точке с абсциссой x=2
ВАРИАНТ № 2
Часть I
1. Вычислить 
2. Найти производную функции 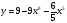 при х= -1
при х= -1
3. Решить уравнение
4. Вычислить, используя формулы приведения
5. Найти производную функции при х=0
6. Вычислить
7. Найдите значение производной в точке х=П/4
8. Найдите значение производной функции в точке
9. Упростите
10.Вычислить , если
11.Найдите угловой коэффициент касательной в точке
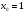
12. Решить уравнение . В ответе укажите наименьший положительный корень уравнения.
13. Упростите
14.Найдите значение производной функции в точке
15. Найти производную функции
ЧАСТЬ II
16. Сколько корней имеет уравнение (соs 5х соs 3х + sin( - 5х)sin(2 + Зх)) = 0?
17. Найдите значение выражения .
18. Основанием прямой призмы служит ромб. Площади диагональных сечений этой призмы равны 25 и 36. Найдите боковую поверхность призмы.
19. Составьте уравнение касательной к графику функции в точке с абсциссой х=2
Ответы 1 части:
| вариант | 1 | 2 |
| 1 | 2,5 | 0,5 |
| 2 | 16,5 | 66 |
| 3 | (-1)п П/3+Пп | +-П/3+2Пп |
| 4 | √3/2 | -√3/2 |
| 5 | 79 | 0 |
| 6 | √3 | √3/2 |
| 7 | 0 | 12 |
| 8 | П | -5 |
| 9 | 1 | Ctg 2a |
| 10 | 3,4 | 3 |
| 11 | -0,875 | -2 |
| 12 | П/8 | П |
| 13 | -2 | 0 |
| 14 | 7 | 2П-1 |
| 15 | 9(3х-2)2 | 9(3х-7)2 |
Используемая литература:
Учебники:
Алгебра и начала математического анализа. 10 класс: учеб. для общеобразоват. учреждений : базовый уровень /[ А.Г. Мордкович, И.М.Смирнова и другие]; – М.: Мнемозина, 2011.
Геометрия. 10-11 классы: учеб. для общеобразоват. учреждений / [Л.С, Атанасян, В.Ф. Бутузов и др.] – М.: Просвещение, 2008.
Методические пособия для учителя:
1.Изучение алгебры и начал математического анализа в 10 классе: кн. Для учителя /Н.Е. Федорова, М.В. Ткачева. – М.: Просвещение, 2008-2010.
2.Алгебра и начала математического анализа: дидакт. материалы для 10 кл. общеобразоват. учреждений: профил. уровень /[М.И. Шабунин, М.В. Ткачева, Н.Е. Федорова, О.Н. Доброва]. –М.: Просвещение,2008.
3. Алгебра и начала математического анализа: дидакт. материалы для 10 кл. общеобразоват. учреждений: базов. уровень /[М.И. Шабунин, М.В. Ткачева, Н.Е. Федорова, О.Н. Доброва]. –М.: Просвещение,2008.
4. Алгебра и начала математического анализа. Тематические тесты. 10 класс: базовый и профил. уровни /М.В. Ткачева, Н.Е. Федорова.- М.: Просвещение, 2009.
5. Задачи по алгебре и началам анализа: Пособие для учащихся 10-11 кл. общеобразоват. учреждений / С.М. Саакян, А.М. Гольдман, Д.В. Денисов. – М.: Просвещение, 2011.

 Получите свидетельство
Получите свидетельство Вход
Вход












 Материал для промежуточной аттестации по математике (алгебра и начала математического анализа, и геометрия) в 10 классах проводится в форме теста (79.08 KB)
Материал для промежуточной аттестации по математике (алгебра и начала математического анализа, и геометрия) в 10 классах проводится в форме теста (79.08 KB)
 0
0 1731
1731 134
134 Нравится
0
Нравится
0


