Получите свидетельство
Вход
Иррациональные уравнения
Иррациональным уравнением называется уравнение, содержащее неизвестное под знаком корня.
При решении иррациональных уравнений применяют метод возведения в степень обеих частей уравнения и метод замены переменной.
При возведении обеих частей уравнения в четную степень возможно появление посторонних корней. В этом случае обязательна проверка найденных корней подстановкой в исходное уравнение. Необходимо иметь в виду, что избавиться от иррациональности вида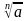 
можно возведением в степень n, так как 
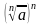=a
1.Простейшие уравнения
1.1)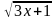
=2 1.2) 
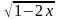=-5
3х+1=4 корней нет
х=1
2.Возведение обеих частей уравнения в степень
2.1)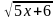 
+ 
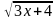=2
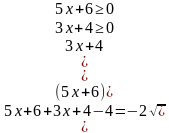
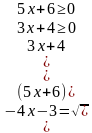
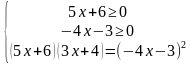
х=-1
3.Замена переменной
3.1)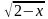
=3х+8
Пусть y=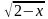 ≥0. Тогда х=2-
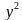и y=3(2- 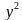)+8
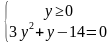y=2 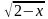=2 х=-2
Упражнения для самостоятельной работы:
1.
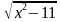= -х-1 Ответ: х=-6
2. 
+
=
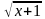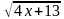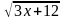Ответ: х=-1
3.
+
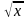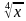= 20 Ответ: х=256
4.
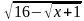= 4 Ответ: х=-1
5. 
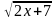– 2 = х Ответ: х=1
Материал для итогового повторения (16.11 KB)
0
30
0
Нравится
0
