


 Муниципальное общеобразовательное учреждение
Муниципальное общеобразовательное учреждение
МОУ СОШ №
Использование проблемных ситуаций на уроках математики в развитии творческого мышления младших школьников
аналитический отчет

Выполнила:
Киселёва С.В.
учитель начальных классов
1 категории
Г. Екатеринбург
2010г.
Оглавление
Введение ……………………………………………………………………...3
Глава 1. Теоретическое обоснование объекта анализа.
Понятие творческого мышления ………………………………6
. Проблема развития творческого мышления …………….........8
Условия формирования творческого мышления младших школьников……………………………………………………......9
Глава 2. Возможности проблемного обучения в развитии творческого мышления учащихся.
2.1 История развития теории проблемного обучения...…………..12
2.2 Современная технология проблемного обучения……………..13
2.3 Реализация и анализ использования проблемных ситуаций
в методике преподавания математики в начальной школе…......................16
Глава 3. Экспериментальное использование проблемных ситуаций на уроках математики и их влияние на развитие творческого мышления младших школьников.
3.1 Изучение творческого мышления младших школьников
с помощью тестов Торренса………………………………………………….22
3.2 Использование проблемных ситуаций на уроках математики
в развитии творческого мышления учащихся………………………………27
3.3.Обработка результатов педагогического исследования…………30
3.4. Рекомендации по совершенствованию процесса формирования творческих способностей младших школьников…………………………...31
Заключение ………………………………………………………………….33
Литература …………………………………………………………………..35
Приложение ………………………………………………………………....36
Введение:
В настоящее время абсолютной ценностью личностно-ориентированного образования является ребенок. И в качестве глобальной цели рассматривают человека культуры: личность свободную, гуманную, духовную, творческую.
Главное в личности – устремленность в будущее, к свободной реализации своих потенций, в особенности творческих, к укреплению веры в себя и возможность достижения идеального «я».
Одной из приоритетных задач современного образования является создание необходимых и полноценных условий для личностного развития каждого ребенка, формирование активной позиции, субъективности учащихся в учебном процессе.
Стремительные изменения в социально – экономических и научно – технических сферах современного общества выдвигают перед образованием принципиально новый социальный заказ: превратить процесс обучения в мощный фактор развития ребенка.
Поставленный заказ логически подводит к определению конечной цели обучения: не снижая планки программных стандартов, развить познавательную активность, сделать процесс обучения средством развития ребенка.
«Концепция модернизации российского образования на период до 2010 года определяет цели общего образования на современном этапе. Она подчеркивает необходимость «ориентации образования не только на усвоение учениками определенной суммы знаний, но и на развитие его личности, его познавательных и созидательных способностей. Общеобразовательная школа должна формировать целостную систему универсальных знаний, умений и навыков, а также самостоятельной деятельности и личной ответственности обучающихся, т.е. ключевые компетентности, определяющие современное качество образования».
В настоящее время существует острая социальная потребность в
творчестве и творческих индивидах. Развитие у школьников творческого мышления одна из важнейших задач в сегодняшней школе. Стремление реализовать себя, проявить свои возможности – это то направляющее начало, которое проявляется во всех формах человеческой жизни – стремление к развитию, расширению, совершенствованию, зрелости, тенденция к выражению и проявлению всех способностей организма и «я».
В своей работе я хочу показать, что в использовании проблемных
ситуаций существуют нераскрытые возможности для развития творческого мышления.
Математика начинается вовсе не со счета, что кажется очевидным, а с… загадки, проблемы. Чтобы у младшего школьника развивалось творческое мышление, необходимо, чтобы он почувствовал удивление и любопытство, повторил путь человечества в познании, удовлетворил с аппетитом возникшие потребности в записях. Только через преодоление трудностей, решение проблем, ребенок может войти в мир творчества. Но почему же именно на проблемное обучение возложена роль в достижении цели: развитие творческого мышления? Какие существуют возможности использования проблемных ситуаций на уроках математики? На эти вопросы будет дан ответ в моей аналитической работе. В связи с этим я выделила:
Объект исследования – развитие творческого мышления школьников на уроках математики.
Предмет исследования – использование проблемных ситуаций на уроках математики в начальной школе как средство развития творческого мышления детей.
Цель исследования: Повышение эффективности обучения младших школьников и развитие их творческого мышления на уроках математики, за счёт использования проблемных заданий.
Задачи:
1) проанализировать психолого-педагогическую литературу по проблеме исследования;
2) раскрыть сущность проблемного обучения и его роль в развитии
творческого мышления младших школьников;
3) проанализировать реализацию проблемного обучения на уроках
математики в начальной школе;
4) выявить, способствует ли проблемное обучение математике развитию творческого мышления школьников;
5) выработать систему мер по совершенствованию творческого мышления младших школьников на уроках математики.
Гипотеза: уровень творческого мышления младших школьников повышается при использовании на уроках математики системы заданий с разной степенью проблемности.
Методы: теоретический анализ психолого-педагогической литературы, тестирование, эксперимент (констатирующий, формирующий), статистическо-математический метод обработки результатов.
Практическая значимость моей исследовательской работы состоит в разработке системы карточек с разной степенью проблемности одного и того же задания для учащихся с разными уровнями творческого мышления.
Программа исследования состояла из естественного психолого-педагогического исследования, включающего три этапа:
Констатирующий – время проведения сентябрь - 2009 г.
формирующий – октябрь - апрель 2009 - 2010 г.
итоговый – сентябрь 2010 г.
Глава 1. Теоретическое обоснование объекта анализа.
1.1. Понятие творческого мышления
Следуя цели и задачам моей работы, я рассматриваю воззрения
разных авторов на творческое мышление, на показатели, которые характеризуют это мышление.
В отечественной психологии широко разрабатываются проблемы творческого мышления человека. Она ставится как проблема продуктивного мышления в отличии от репродуктивного. Психологи единодушны в признании того, что в любом мыслительном процессе сплетены продуктивные и репродуктивные компоненты. Большое внимание уделяется раскрытию сущности творческого мышления, выявлению механизмов творческой деятельности и природы творческого мышления. Я.А. Пономарев, В.Н. Дружинин, В.Н. Пушкин и другие отечественный психологи считают основным признаком мышления рассогласование цели (замысла, программы) и результата. Творческое мышление возникает в процессе осуществления и связана с порождением «побочного продукта», который и является творческим результатом.
Выделяя признаки творческого акта, все исследователи подчеркивают его бессознательность, неконтролируемость волей и разумом, а также измененность состояния сознания.
Второй признак творческого мышления – спонтанность, внезапность творческого акта от внешних ситуативных причин.
Таким образом, главная особенность творческого мышления связана со спецификой протекания процесса в целостной психике как системе, порождающей активность индивида.
Иное дело – оценка продукта как творческого. Здесь в силу вступают социальные критерии: новизна, осмысленность, оригинальность и так далее.
С творческим мышлением сопряжены два личностных качества:
интенсивность поисковой мотивации и чувственность к побочным образованиям, которые возникают при мыслительном процессе.
И.Я. Лернер считает, что основу творческого мышления представляют следующие черты:
самостоятельный перенос знаний и умений в новую ситуацию;
видение новых проблем в знакомых, стандартных условиях;
видение новой функции знакомого объекта;
видение структуры объекта, подлежащего изучению, то есть быстрый, подчас мгновенный охват частей, элементов объекта в их соотношении друг с другом;
умение видеть альтернативу решения, альтернативу подхода к его поиску;
умение комбинировать ранние способы решения проблемы в новый способ;
умение создавать оригинальный способ решения при известности других.
Овладев этими чертами, можно развивать их до уровня, обусловленного природными задатками и усердием. Однако перечисленным чертам свойственна одна способность – «они не усваиваются в результате получения информации или показа действия, их нельзя передать иначе как включением в посильную деятельность, требующую проявления тех или иных творческих черт и тем самым эти черты формирующую»
Итак, в отечественной психологии исследования творческого мышления теоретически обоснованы, индивидуальные различия анализируются не только с количественной стороны, но и качественной стороны. Тем не менее, все еще незначительно количество исследований в этой области.
Таким образом, творческое мышление – мышление, связанное с созданием или открытием принципиально нового субъективного знания, с генерацией собственных оригинальных идей.
Показателем, характеризующим творческое мышление, и на которое я буду основываться в своем исследовании, является следующее: беглость, гибкость и оригинальность мысли.
Беглость включает в себя два компонента: легкость мышления, то есть быстрота переключения текстовых заданий и точность выполнения задания.
Гибкость мыслительного процесса – это переключение с одной идеи на другую. Способность найти несколько различных путей решения одной и той же задачи.
Оригинальность – минимальная частота данного ответа к однородной группе.
1.2. Проблема развития творческого мышления
В психологии развития существуют три подхода к проблеме развития творческого мышления:
1) генетический, отводящий основную роль наследственности;
2) средовой, представители которого считают решающим фактором развития внешние условия;
3) генотип – средового взаимодействия, сторонники которого выделяют разные типы адаптации индивида к среде в зависимости от наследственных черт.
В.Н. Дружинин, В.И. Тютюнина и другие считают необходимым для развития творческого мышления:
- отсутствие регламентации предметной активности, точнее – отсутствие образца, регламентированного поведения;
- наличие позитивного образца творческого поведения;
- создание условий для подражания творческому поведению и
планированию проявлений агрессивного и деструктивного поведения;
- социальное подавление творческого поведения.
Существуют два направления проблемы развития творческого мышления:
- влияние условий воспитания и повседневной жизни;
- проведение развивающего эксперимента.
Развитие совершается в процессе обучения и воспитания. Оно формируется в процессе взаимодействия с миром, посредством овладения в процессе обучения содержания материальной и духовной культуры, искусства. Поэтому есть возможность говорить о специальном, целенаправленном формировании творческого мышления, о системном формирующем воздействии. Но каковы же условия формирования творческого мышления?
1.3. Условия формирования творческого мышления младших школьников
Важную роль в подготовке к творческому труду играет начальная школа. Именно в младшем школьном возрасте заключается психологическая основа для такой деятельности. Развиваются воображение и фантазия, творческое мышление, воспитывается любознательность, формируются умения наблюдать и анализировать явления, проводить сравнения, обобщать факты, делать выводы, практически оценивать деятельность, активность, инициативность. Начинают складываться и дифференцироваться интересы, склонности, формируются потребности, лежащие в основе творчества.
Отличительный признак творческой деятельности детей – субъективная новизна продукта деятельности. По своему объективному значению «открытие» ребенка может быть и новым, необычным, но в то же время выполняться по указке учителя, по его задумке, с его помощью, а потому не являться творчеством. И в то же время ребенок может предложить такое решение, которое уже известно, использовалось на практике, но додумался до него самостоятельно, не копируя известное.
В этом случае мы имеем дело с творческим процессом, основанным на догадке, интуиции, самостоятельном мышлении ученика. Здесь важен сам психологический механизм деятельности, в которой формируется умение решать нешаблонные, нестандартные математические задачи.
Успешное формирование у младших школьников творческого мышления возможно лишь на основе учета педагогом основных особенностей детского творчества и решения центральных задач в развитии творческого мышления. Для того чтобы сформировать у учащихся умения творчески решать математические задачи, необходимо прежде всего позаботиться о развитии у них математического кругозора, о создании реальной чувственной основы для воображения.
Развитие творческого мышления неотделимо от формирования исполнительских умений и навыков. Чем разностороннее и совершеннее умения и навыки учащихся, тем богаче их фантазия, реальнее их замыслы, тем более сложные математические задания выполняют дети.
Психологами установлено, что развитие мышления человека неотделимо от развития его языка. Поэтому важнейшая задача в развитии творческого мышления учащихся – обучение их умению словесно описывать способы решения задач, рассказывать о приемах работы, называть основные элементы задачи, изображать и читать графические изображения ее. Усвоение учащимися необходимого словарного запаса очень важно для формирования и развития у них внутреннего плана действия. При всяком творческом процессе задача решается сначала в уме, а затем переносится во внешний план.
Условия для формирования творческого мышления учащихся:
- доминирование развивающих возможностей учебного материала над его информационной насыщенностью;
- сочетание условия развития продуктивного мышления с навыками его практического использования;
- доминирование собственной исследовательской практики над
репродуктивным усвоением знаний;
- формирование способностей к критичности и лояльности в оценке идей;
- стремление к максимально глубокому исследованию проблемы;
- высокая самостоятельность учебной деятельности, самостоятельный поиск знаний, исследование проблем;
- индивидуализация – создание условий для полноценного проявления и развития специфичных личностных функций субъектов образовательного процесса;
- проблематизация – ориентация на постановку перед детьми проблемных ситуаций.
Таким образом, соблюдение этих условий даст возможность формирования творческого мышления школьников.
Для дальнейшей исследовательской работы я выделила три основных
условия формирования творческого мышления, три стратегии:
1) индивидуализация образования;
2) исследовательское обучение;
3) проблематизация.
Глава 2. Возможности проблемного обучения в развитии творческого мышления учащихся
2.1. История развития теории проблемного обучения
Идея активизации обучения имеет большую историю. Еще в древние времена было известно, что умственная активность способствует и лучшему запоминанию, и более глубокому проникновению в суть предметов, процессов и явлений. В основе стремления к побуждению интеллектуальной активности учащихся лежат определенные философские взгляды. Постановка проблемных вопросов собеседнику и его затруднение в поисках ответов на них были характерны для дискуссий Сократа, этот же прием был известен в пифогорейской школе.
Согласно философским и психологическим воззрениям , мыслить человек начинает тогда, когда сталкивается с трудностями, преодоление которых имеет для него большое значение. В каждом полном акте мышления выделяются следующие ступени:
- ощущение трудности;
- ее обнаружение и определение;
- выдвижение замысла ее разрешения (формулировка гипотезы);
- формулировка выводов, следующих из предполагаемого решения (логическая проверка гипотезы);
- последующие наблюдения и эксперименты, позволяющие принять или отвергнуть гипотезу.
Впоследствии, за «трудностями», которые нужно преодолеть, размышляя над поиском решения, закрепилось название «проблем».
Условиями успешности обучения являются: проблематизация учебного материала (знания дети удивления и любопытства); активность ребенка (знания должны усваиваться с аппетитом); связь обучения с жизнью ребенка, игрой, трудом. Таким образом, проблемное обучение – это такая организация учебных занятий, которая предполагает создание под руководством учителя проблемной ситуации и активной самостоятельной деятельности учащихся по их разрешению, в результате чего и происходит творческое овладение профессиональными знаниями, умениями и навыками, развитие мыслительных способностей.
2.2. Современная технология проблемного обучения
Будущее образования находится в тесной связи с перспективами проблемного обучения. И цель проблемного обучения широкая: усвоение не только результатов научного познания, но и самого пути процесса получения этих результатов; она включает еще и формирование познавательной самостоятельности ученика и развития его творческих способностей (помимо овладения системой знаний, умений, навыков и формирования мировоззрения).
Итак, проблемное обучение – это современный уровень развития дидактики и передовой педагогической практики. Проблемным называется обучение потому, что организация учебного процесса базируется на принципе проблемности, а систематическое решение учебных проблем – характерный признак этого обучения.
Проблемная ситуация и учебная проблема являются основными понятиями проблемного обучения. Учебная проблема понимается как отражение логико-психологического противоречия процесса усвоения, определяющее направление умственного поиска, пробуждающее интерес к исследованию сущности неизвестного и ведущее к усвоению нового понятия или нового способа действия. Существует две основные функции учебной проблемы:
1) определение направления умственного поиска, то есть деятельности ученика по нахождению способа решения проблемы;
2) формирование познавательных способностей, интереса, мотивов
деятельности ученика по усвоению новых знаний.
Для учителя она является средством управления познавательной деятельностью ученика; формирование его мыслительных способностей.
В деятельности ученика – служит стимулом активизации мышления, а процесс ее решения – способом превращения знаний в убеждения.
Проблемная ситуация – средство организации проблемного обучения, это начальный момент мышления, вызывающий познавательную потребность учения и создающий внутренние условия для активного усвоения новых знаний и способов деятельности.
Проблемная ситуация может быть различной. По содержанию неизвестного проблемные ситуации делятся: неизвестная цель; неизвестен объект деятельности; неизвестен способ деятельности; неизвестны условия выполнения деятельности.
По уровню проблемности:
I. возникающие независимо от приемов;
II. вызываемая и разрешаемая учителем;
III. вызываемая учителем, разрешаемая учеником;
IV. самостоятельное формирование проблемы и ее решение.
По виду рассогласования информации: неожиданности; конфликта; предположения; опровержения; несоответствия; неопределенности.
По методическим особенностям: непреднамеренные; целевые; проблемное изложение; эвристическая беседа; проблемные демонстрации; игровые проблемные ситуации; исследовательская лабораторная работа; проблемный фронтальный эксперимент; мысленный проблемный эксперимент; проблемное решение задач; проблемные задания.
Особенность проблемных методов состоит в том, что методы основаны на создании проблемных ситуаций, активной познавательной деятельности учащихся, состоящих в поиске и решении сложных вопросов, требующих актуализации знаний, анализа, умений видеть за отдельными фактами явления и закон.
В современной теории проблемного обучения различают два вида проблемных ситуаций: психологические и педагогические. Первая касается деятельности учеников, вторая представляет организацию учебного процесса.
Педагогическая проблемная ситуация создается с помощью активизирующих действий, вопросов учителя, подчеркивающих новизну, важность, красоту и другие отличительные качества объекта познания. Создание психологической проблемной ситуации сугубо индивидуально. Ни слишком трудная, ни слишком легкая познавательная задача не создает проблемы для учеников. Проблемная ситуация может создаваться на всех этапах процесса обучения: при объяснении, закреплении, контроле.
Учитель создает проблемную ситуацию, направляет учащихся на ее решение, организует поиск решения. Таким образом, ребенок становится в позицию своего обучения и как результат у него образуются новые знания, он овладевает новыми способами действия. Трудность управления проблемным обучением состоит в том, что возникновение проблемной ситуации – акт индивидуальный, поэтому от учителя требуется использование дифференцированного и индивидуального подхода.
Для реализации проблемной технологии необходимо:
- отбор самых актуальных, сущностных задач;
- определение особенностей проблемного обучения в различных видах учебной работы;
- построение оптимальной системы проблемного обучения, создание учебных и методических пособий и руководств;
- личностный подход и мастерство учителя, способные вызвать активную познавательную деятельность ребенка.
2.3. Реализация и анализ использования проблемных ситуаций в методике преподавания математики в начальной школе
Уже в дошкольном возрасте жизнь ставит перед детьми бесчисленные математические проблемы. С момента прихода ребенка в школу функции «жизни» принимает школа; она становится ответственной за то, получит ли ребенок соответствующую подготовку, приучится ли к математическому мышлению, научится ли отыскивать и решать математические проблемы.
На уровне начального обучения, то есть в 1-4 классах, дети сталкиваются с многочисленными проблемными ситуациями, которые побуждают их к математическому мышлению. Уже простое распределение тетрадей, учебников может стать для учащихся первого класса проблемой, если мы их спросим, хватит ли учебных принадлежностей для всего класса. Видя относительно небольшую пачку тетрадей, дети, по всей вероятности, будут думать, что их не хватит, ибо имеют в виду величину тех и других элементов. Проверкой правильности предположения детей будет раздача тетрадей. Указанная проблема является примером сравнения одного множества с другим и оценки количества единиц множества.
Проблемность при обучении математики возникает совершенно естественно, не требуя никаких специальных упражнений, искусственно подбираемых ситуаций. В сущности, не только каждая текстовая задача, но и добрая половина других упражнений, представленных в учебниках математики и дидактических материалах, и есть своего рода проблемы, над решением которых ученик должен задуматься, если не превращать их выполнения в чисто тренировочную работу, связанную с решением по готовому, данному учителем образцу.
Учитель нередко наносит ущерб делу, разучивая с детьми способы решения задач определенных видов, предлагая подряд большое число однотипных упражнений, каждые из которых, будучи предъявлено среди упражнений других видов, без дополнительных объяснений, могло бы послужить для отталкивания собственной мысли учащихся.
Проблемное обучение, а не преподнесение готовых, годных лишь для заучивания фактов и выводов всегда вызывает неослабевающий интерес учеников. Такое обучение заставляет искать истину и всем коллективом находить ее. В проблемном обучении на общее обсуждение ставится вопрос-проблема, содержащий в себе иногда элемент противоречий, иногда неожиданности. Проблемное обучение вызывает со стороны учащихся живые споры, обсуждения. Проблемное обучение вызывает к жизни эмоции учеников, создается обстановка увлеченности, раздумий, поиска. Это плодотворно сказывается на отношении школьника к учению. Для развития познавательных интересов важно усложнение познавательных задач. Для этого интересно использовать предварительную подготовку к восприятию нового.
Упражнения в решении составных текстовых задач, в сравнении выражений, требующие использования известных детям закономерностей и связей в новых условиях, упражнения геометрического содержания, которые часто требуют переосмысления приобретенных ранее знаний, и другие должны быть использованы для постановки детьми проблемных задач. Только в этом случае обучение математике будет оказывать действенную помощь в решении образовательных, воспитательных и развивающих задач обучения, способствуя развитию познавательных способностей учащихся, таких черт личности, как настойчивость в достижении поставленной цели, инициативность, умение преодолевать трудности.
Введение математических понятий представляет также много возможностей для организации проблемных ситуаций в классе. Например, ученик получил задания: «К 2 прибавь 5 и помножь на 3». И другое: «К 2 прибавь 5, помноженное на 3». Можно записать обе задачи и вычислить следующим образом:
2+5*3=21
2+5*3=17
Такая запись вызывает удивления у детей. После анализа действий учащиеся приходят к выводу, что два разных результата могут быть правильным и зависит от того, в какой очередности выполнять сложение и умножение. Возникает проблемный вопрос, как записать этот пример, чтобы получить правильный ответ. Вопрос побуждает детей к поискам, в результате чего они приходят к понятию скобок. После вписывания скобок, задача принимает вид:
(2+5)*3=21
2+5*3=17
Другой пример задания связан с геометрическим материалом. Учитель предлагает вниманию первоклассников плакат, на котором изображены несколько четырехугольников и пятиугольников. Все эти фигуры на плакате никак не сгруппированы, но четырехугольники окрашены в красный цвет, а пятиугольники – в зеленый. Я сообщаю, что все красные фигуры можно назвать четырехугольниками, а зеленые – пятиугольниками. После этого перед классом ставится проблемный вопрос: «Как вы думаете, почему красные фигуры можно назвать четырехугольниками, а зеленые – пятиугольниками?». Для решения данной проблемы дети должны провести ряд наблюдений, сопоставлений, сравнений. Они должны сравнивать мысленно термины «четырехугольник» и «пятиугольник». Анализируя эти слова, они должны расчленить их, выделив в них знакомые им слова, являющиеся частями новых терминов – «четыре» и «угол», «пять» и «угол». Такой анализ уже может направить их мысль в определенном направлении. Проверить правильность возникших предположений они смогут, обратившись к внимательному рассматриванию предложенных им фигур. Здесь снова придется провести ряд наблюдений, сопоставлений, сравнений, в результате которых они должны убедиться, что действительно все красные фигуры содержат по четыре угла, а зеленые – по пять углов. Подметив эту особенность, сопоставив ее с особенностями терминов-названий данных фигур, дети должны прийти к выводу, который и будет ответом на поставленный проблемный вопрос.
Любая составная текстовая задача ставит ученика перед определенными трудностями, требующими значительного умственного усилия при выполнении мыслительных операций, приводящих к решению. Проблемные текстовые задачи ставят ученика в ситуацию, в которой у него должно появиться удивление и ощущение трудности, или одно только ощущение трудности, которое, однако, ученик намерен преодолеть. Если эти условия отсутствуют, то задача им уже перестала быть для него проблемной, или еще не может быть ею в связи с тем,
что он не владел в достаточной степени средними ступенями, дающими возможности для преодоления данной трудности.
Решение составной текстовой задачи нового вида (содержащей новую для учащихся комбинацию известных уже видов простых задач) требует выполнения всех тех элементов продуктивного мышления, которые свойственны исследовательскому подходу: это и наблюдение, и изучение фактов (анализ условия, выделение числовых данных, осознание вопроса), и выявление промежуточных неизвестных (на основе анализа связей, существующих между искомыми и данными), и составление плана решения (при составлении которого могут возникнуть различные направления поиска ответа, могут быть найдены различные способы решения), и осуществление этого плана с использованием имеющихся данных и приобретенных ранее знаний, умений и навыков. Это и формулировка ответа, и проверка выполненного решения.
Проблемы, заключающиеся в математической текстовой задаче приводит к тому, что эта задача выступает перед учеником как целостная ситуация – с теми элементами, которые имеются для выполнения этой ситуации (данные), и теми, которые имеются для внесения ее решения (неизвестное). Она может быть закрытой проблемой, и тогда в задаче нет недостатка в данных, или открытой, где решение нельзя довести до конца или ученик сам должен собрать эти данные.
Изучение мною этой типологии – важное условие создания проблемных ситуаций при изучении нового материала, повторении пройденного и при формировании умений и навыков. Вот некоторые из них:
- задачи с не сформулированным вопросом;
- задачи с недостающими данными;
- задачи с излишними данными;
- задачи с несколькими решениями;
- задачи с меняющимся содержанием;
- задачи на соображение, логическое мышление.
Таким образом, постановка вопроса об использовании проблемных ситуаций не является новой для меня, а требуют лишь правильного использования всех тех ресурсов, которые скрыты в начальном курсе математики. Но не всякий материал может служить основой для создания проблемной ситуации. К непроблемным элементам учебного материала относится вся конкретная информация, содержащая цифровые и качественные данные; факты, которые нельзя «открыть». Непроблемны все задачи, решаемые по образцу, по алгоритму, по известному способу.
Проблемное обучение возможно применять для усвоения обобщенных знаний – понятий, правил, законов, причинно-следственных и других логических зависимостей.
В силу того, что проблемный путь получения знаний всегда требует больших затрат времени, чем сообщение готовой информации, нельзя говорить вообще о переходе на проблемное обучение.
В обучении всегда будут нужны и тренировочные задачи, и задания, требующие воспроизведения знаний, способствующие запоминанию необходимого и т.п. Лишь сравнительно небольшая часть новых знаний должна приобретаться способом самостоятельных открытий, поэтому я говорю здесь только об использовании элементов проблемного обучения. Оптимальной структурой учебного материала будет являться сочетание традиционного изложения с включением проблемных ситуаций. Важно и то, что проблемное обучение, приучающее учащихся сталкиваться с противоречиями, разбираться в них, искать решение, является одним из средств формирования диалектического мышления.
Итак, постановка вопроса о реализации и анализе использования проблемных ситуаций не является новой в методике преподавания математики, а требует лишь правильного использования всех тех ресурсов, которые скрыты в начальном курсе математики.
Глава 3. Экспериментальное использование проблемных ситуаций на уроках математики и их влияние на развитие творческого мышления младших школьников.
3.1. Изучение творческого мышления младших школьников
с помощью тестов Торренса
Первый этап экспериментального исследования состоит в изучении творческого мышления младших школьников, то есть констатирующий эксперимент.
Было проведено тестирование на выявление уровня творческого учащихся, их гибкости, беглости и оригинальности. Были использованы тесты Торренса.
Е.П. Торреснс, создавший наиболее известные тесты креативности, обратил основное внимание не на продукты, а на сам процесс творческого мышления. Тесты Е.П. Торренса были разработаны в связи с задачами образования, как часть продолжительной исследовательской программы, методической работы с учащимися, стимулирующей их творческие способности.
Показатели по всем частям текста определяются факторами, установленными в исследованиях Дж. Гилфорд, а именно: легкость, гибкость, оригинальность и точность.
Тесты Е.П. Торренса созданы в 1966 году. Все тесты сгруппированы в вербальную и невербальную батареи. Первая батарея обозначается как словесное творческое мышление, вторая – изобразительное творческое мышление. С тем, чтобы избежать беспокойства испытуемых и создать благоприятную психологическую атмосферу, тесты называются занятиями, и, как все время подчеркивается в инструкциях, занятиями веселыми. Тесты предназначены для использования в детском саду и во всех классах школы, хотя до 4 класса их нужно предъявлять индивидуально и устно.
Тест Е.П. Торренса на вербальное творческое мышление предназначен для диагностики у детей таких характеристик, как умение задавать информативные вопросы, устанавливать возможные причины и следствия применительно к ситуациям, изображенным на серии картинок, предлагать оригинальные способы применения обычных предметов, задавать нестандартные вопросы по поводу хорошо знакомого предмета, строить предложения.
Невербальными тестами предусматривается выполнение испытуемыми таких заданий, как конструирование картин (на основе изображения ярко раскрашенной фигуры неправильной формы), завершение картинки, использование параллельных линий или кругов для оставления изображений. Надежность тестов очень велика – от 0,7 до 0,9. Вербальные более надежны, чем изобразительные.
Тест «Дорисовывание» для исследования невербального творческого мышления у детей 4-10 лет.
Стимульный материал. Листы белой бумаги, в середине которых простым или черным карандашом нарисованы контуры.
Инструкция. Посмотри на этот листок. Кто-то из ребят начал рисовать, но не успел закончить. Подумай, что из этого может получиться и закончи, пожалуйста, рисунок.
Проведение теста. Детям даю только простой или черный карандаш. Я не вмешиваюсь в процесс рисования и на возможные вопросы детей отвечаю, что они могут рисовать все, что им хочется. Для дорисовывания детям обычно предлагаю по очереди 5-6 контуров (по мере выполнения). После выполнения каждого задания я спрашиваю ребенка, что именно нарисовано на картинке, однако при возникновении затруднения не настаиваю на ответе.
Анализ результатов. При интерпретации полученных данных обращаю внимание на беглость, гибкость и оригинальность полученных ответов.
Беглость связываю с общим количеством ответов. Максимальное количество баллов – 3, минимальное – 0 (если ребенок отказывается рисовать). Гибкость оцениваю по количеству использованных категорий в содержании рисунков (например, ребенок рисует только людей или и людей, и животных, и разнообразные предметы). Отказ от задания – 0 баллов, максимальное количество баллов – 3 (при использовании нескольких категорий). Оригинальность разных категорий оцениваются по баллам:
1 – звери, пища, транспорт;
2 – игрушки, человек;
3 – герои сказок, одежда, птица, растения;
4 – мебель, рыбы;
5 – насекомые, техника;
6 – предметы туалета, светильники, музыкальные инструменты, постельные принадлежности.
Кроме беглости, гибкости и оригинальности, оцениваю и характер рисунка – важный показатель творческих способностей ребенка. При отказе рисовать, воспроизведение тождественного контура рядом с основным, прикрепление овала к бумаге без называния рисунка и дорисовывания – 0 баллов. Дорисовывание с минимальным количеством линий, при котором обыгрывается традиционное использование контура (огурец, солнышко, шарик, волны) – 1 балл. Рисунок состоит из дополнительных элементов, соединенных с основным контуром (человек, кораблик, дорожка в саду) – 2 балла. Основной контур является частью в других предметах или их деталью (включение) – 3 балла. Рисунок содержит определенный сюжет, выражает некоторые действия – 4 балла. Рисунок включает в себя несколько персонажей или предметов, раскрывающих его тему, которая подчинена одному смысловому центру, связанному с основным контуром – 5 баллов.
В норме дети набирают 6-9 баллов, получив 1-2 балла за беглость, гибкость и оригинальность и 3-4 балла за характер рисунка. Норма не зависит от возраста, который влияет только на изменение стимульного материала. При большом количестве баллов (11 и выше) можно говорить о высоком уровне творческого мышления ребенка, его одаренности. Дети, набравшие меньше 2-3 баллов, фактически не обладают творческим мышлением, хотя могут иметь высокий интеллектуальный уровень.
Тест для детей 7-10 лет, с помощью которого исследуют одновременно и невербальное и вербальное творческое мышление.
Стимульный материал. 15 кружков, нанесенных рядами, по 5 в каждом на листе белой бумаги.
Инструкция. Посмотри на эти кружочки. Тебе надо дорисовать каждый из них так, чтобы получилась какая-то картина. Картинки эти должны быть связаны между собой и служить иллюстрацией какого-то рассказа, сюжет которого разворачивается в той же последовательности, в которой расположены картинки на бумаге.
Проведение теста. После инструкции детям даю лист бумаги с написанными на нем кружочками и простой карандаш. Время работы не должно превышать 15 минут. После окончания работы детей прошу дать название рассказать и передать его содержание. При рассказе дети должны пользоваться сделанными рисунками в качестве своеобразной схемы рассказа. Если какой-то кружок пропущен, я указываю ребенку на эту ошибку и даю ему возможность исправить ее по ходу дела. Если ребенок не может справиться с заданием полностью (нет ни рассказа, ни рисунков) или частично (есть либо рассказ, либо рисунок, или рисунки и рассказ не совпадают между собой), я ему помогаю, а может даже могу и прервать тест.
Анализ результатов. Рисунки оцениваю так же, как в тесте «Дорисовывание». Рассказ оценивается по показателям – гибкость, беглость и оригинальность, а также по общему содержанию.
Содержание рассказа оценивается следующим образом – при отказе от работы – 0 баллов. Если вместо цельного рассказа ребенок может сказать только о содержании отдельных рисунков-кружочков – 1 балл. При наличии нескольких не связанных друг с другом эпизодов, каждый из которых объединяет в единое целое несколько рисунков – 2 балла. Использование заимствованного сюжета (известного рассказа, сказки) для увязывания рисунков во всех 15 кружочках – 3 балла. Оригинальный сюжет, объединяющий все рисунки – 4 балла. Важно рассматривать как качество рисунков (образная креативность), так и содержание рассказа (вербальная креативность).
Тест «Что может быть одновременно» для диагностики 7-10 летних детей направлен на исследование вербального творческого мышления.
Стимульный материал. Набор вопросов, которые по очереди задаю ребенку.
Что может быть одновременно:
1 - живым и неживым;
2 – черным и белым;
3 – маленьким и большим;
4 – мягким и твердым;
5 – легким и тяжелым;
6 – горячим и холодным
7 – кислым и сладким.
Инструкция. Я тебе сейчас буду задавать вопросы, на которые должен мне ответить как можно быстрее.
Проведение теста. Детям по очереди задаю вопросы: Что может быть одновременно белым и черным? Сладким и кислым? И так далее. Если ребенок не понял вопроса и дает два ответа, ему напоминаю, что речь идет об одном предмете, который может в одно и то же время быть, например и белым, и черным, а не о двух предметах, один из которых белый, а другой – черный. В случае повторных ошибок или отказа отвечать тестирование прерываю.
Анализ результатов. При анализе подсчитываю количество баллов по следующим параметрам: беглость и оригинальность. Как правило, дети набирают 3-4 балла, что является средним уровнем креативности.
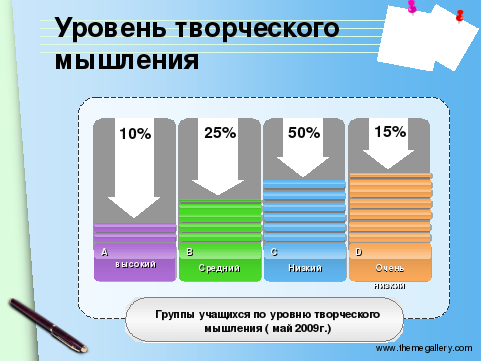
Определив уровень творческого мышления учащихся (см. Приложение №1) их гибкость, беглость и оригинальность, я разделила детей на четыре группы:
- высокий уровень мышления (12 баллов) – 2 человека;
- средний уровень мышления (10-11 баллов) – 5 человек;
- низкий уровень мышления (7-9 баллов) – 6 человек;
- очень низкий уровень мышления (6 баллов) – 7 человек.
3.2. Использование проблемных ситуаций на уроках математики в развитии творческого мышления учащихся
В последнее время учителя начальных классов довольно часто при изучении математики создают на уроках проблемные ситуации. Однако чаще всего после создания ситуации учитель сам сообщает новые знания. Такой способ подачи нового материала не обеспечивает активности мыслительной деятельности большинства, а тем более всех учащихся. Это происходит потому, что как правило, поставленную проблему решают и раскрывают классу сильные учащиеся, в то время как средние и слабые только приступают к решению.
Значит, в таких условиях самостоятельно усваивают знания в основном сильные учащиеся, остальные получают их в готовом виде от своих товарищей. Таким образом, несмотря на то, что организация проблемных ситуаций в целом дает повышение эффективности обучения, она не активизирует умственную деятельность большинства учащихся.
Для обеспечения развития творческого мышления учащихся в проблемном обучении необходима оптимальная последовательность ситуаций, их определенная система. Поэтому при организации проблемного обучения мною были выделены четыре уровня проблемности. Уровни проблемности отличаются степенью обобщенности задач, предложенных учащимся для решения, и степенью помощи, подсказки со стороны учителя. Четыре уровня проблемности:
- высокий;
- средний;
- низкий;
- очень низкий.
По сути дела представляют собой несколько вариантов одного и того же задания. Начиная с самого высокого уровня проблемности и постепенно снижая трудность задания, я помогаю каждому ученику решить проблему, корректируя ход решения проблемы каждым учеником.
Сущность уровней проблемности заключается в следующем. Проблемная задача, сформулированная на самом высоком уровне, не содержит подсказки; на высоком уровне содержит одну подсказку; на среднем уровне – две подсказки. Проблемная задача, сформулированная на низком уровне, содержит ряд последовательно предполагаемых заданий и вопросов, которые постепенно подводят учащихся к выводу.
Проблемные уроки проводились по следующей схеме. Сначала я ставлю для всех общую проблему, формулирую последовательно на всех уровнях проблемности, начиная с самого высокого. Чтобы определить, кто в состоянии вывести правило «Порядок действий в выражениях со скобками» (см. Приложение №2), на каждом из четырех уровней проблемности, как ученик шел к открытию правила, учащиеся должны фиксировать результаты своих попыток вывести правило, записать его на листочках, ставя порядковый номер проблемности. Это дает возможность мне контролировать работу каждого ученика на всех этапах вывода правила. Если учащиеся выводили и фиксировали правило на самом высоком или последующих уровнях проблемности кроме низкого, они и в дальнейшем должны были продолжать работу над правилом: проверять формулировку в соответствии с показами и, если нужно, уточнять и совершенствовать ее.
В случае, когда отдельные ученики не справляются с заданием ни на одном уровне проблемности, я имею возможность определить характер затруднений, их причины и своевременно помочь; вместе с тем я имею возможность формировать у детей соответствующие операции, развивать творческое мышление.
После того как учащиеся записали формулировку правила при постановке задания на низком уровне проблемности, я спрашиваю некоторых из них, какое они правило вывели, прошу произнести это правило в их формулировке. Вслед за этим я формулирую правило так, как оно дано в учебнике, и только после этого сообщаю, какое правило изучено, записываю тему на доске. Закрепление знаний и формирование умений и навыков провожу в форме письменного и устного выполнения упражнений из учебника.
Такая организация работы отнимает немало времени, однако она рациональна: во-первых, все дети, используя помощь учителя, должны думать и писать, совершенствуя формулировку; во-вторых, я имею возможность проанализировать попытки, ход открытия правила каждым учеником, то есть выявить индивидуальные особенности мыслительной деятельности; в-третьих, каждый ученик убеждается в том, что если будет внимательным, подумает, применит имеющиеся знания, то обязательно справится с заданием; в-четвертых, мои подсказки направляют мысль ученика, помогают овладеть мыслительными операциями: сравнением, анализом, синтезом, обобщением, при этом ученики, которые овладели мыслительными операциями, упражняются в них, а другие обучаются им постепенно; в-пятых, воспитываются ценные качества личности – способность к напряженному умственному труду, самостоятельность, пытливость, трудолюбие; в-шестых, формулируется математическая зоркость, устойчивость, устойчивые математические навыки, развивается творческое мышление.
При такой организации проблемного урока нет изначального деления учащихся на «сильных», «средних» и «слабых» - задание всем одинаковое;
конечный результат – формулировка правила на одном из уровней проблемности
– показатель уровня самостоятельности и развитие мыслительной деятельности, уровня развития творческого мышления учащихся.
После изучения правила на следующем уроке провожу проверку:
а) знания формулировки правила «Порядок действий в выражениях со скобками»;
б) степени сформированности умений и навыков в виде самостоятельности проверочной работы.
Приведу примеры заданий на разных уровнях проблемности во II классе. (см. Приложение №2)
3.3. Обработка результатов педагогического исследования
Для проверки статистических данных данной гипотезы на основе результатов измерений некоторых свойств объектов в математической статистике разработаны специальные методы, основанные на результатах измерений свойств объектов двух зависимых выборок.
Учащиеся выполняли тесты Торренса, направленные на проверку их уровня творческого мышления.
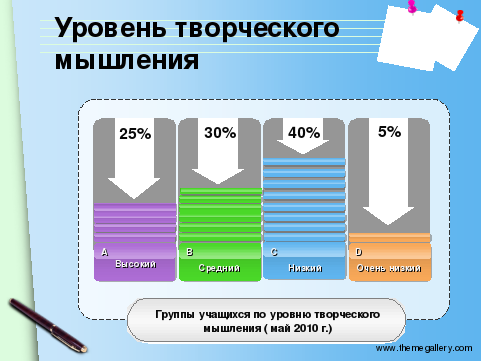
Затем была проведена система уроков проблемного характера. После этого учащиеся выполнили те же тесты, которые оценивали по двенадцатибальной системе.
Данный эксперимент проводился с целью проверки эффективности использования проблемных ситуаций на уроке математики как средства повышения уровня мышления школьников.
Что позволяет сделать вывод о повышении уровня творческого мышления, а следовательно и их развития, после серии уроков математики с использованием проблемных ситуаций (системы карточек с разной степенью проблемности одного и того же задания).
3.4. Рекомендации по совершенствованию процесса формирования творческих способностей младших школьников
Для развития у ребенка творческого мышления необходимы различные подходы, способствующие созданию условий для реализации у учащихся своих задатков. Особенно эффективными могут быть занятия во внеурочное время, в группе продленного дня. Такие занятия следует проводить регулярно, как занятия – факультативы по математике, где всем детям независимо от их уровня творческого мышления, будет интересно.
Дети, хорошо успевающие, смогут в еще большей степени развернуть свое творческое мышление, а слабоуспевающие, решая нестандартные задачи, посильные для них, смогут обрести уверенность в своих силах, научиться управлять своими поисковыми действиями, подчинять их определенному плану.
В этих условиях у детей развиваются такие важные качества мышления, как глубина, критичность, гибкость, которые являются сторонами его самостоятельности. Только развитие самостоятельного мышления, творческого, поискового, исследовательского есть основная задача начального обучения.
Развитие самостоятельного, творческого мышления, проявляющегося, в частности, в своеобразном видении ребенком проблемной ситуации, требует индивидуального подхода, который бы учитывал особенности мыслительной деятельности каждого ученика.
Формирование творческого мышления предполагает решение детьми негативных, нестандартных задач, имеющих несколько способов решения. Для того чтобы решение таких задач способствовало действительному развитию творческого мышления, оно должно быть организовано особым образом. В частности, необходимо провести разбор наиболее распространенных ошибок, которые встретились при решении, обсуждении разных способов решения, их обоснование и критику.
Этому послужит организация регулярных занятий во внеклассной работе, на занятиях факультатива по математике, дети решают нестандартные задачи, предлагаемые в определенном порядке, от простых к сложному, а не случайным образом, когда детям предлагают решать задачи учебного содержания или различного рода головоломки.
Заключение
В завершении своей работы подведу итог.
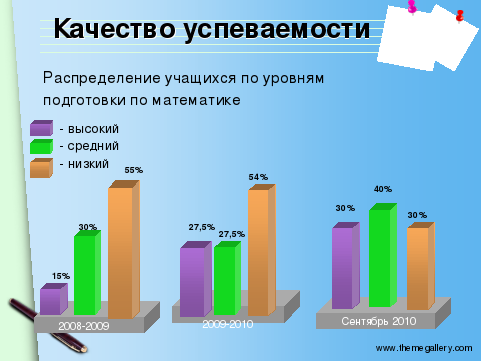
В результате исследования я подтвердила правильность выдвинутой мною гипотезы: при использовании системы карточек с разной степенью проблемности на уроках математики повышается уровень творческого мышления младших школьников.
Все поставленные задачи исследования выполнены. Теоретически сущность проблемного обучения и его роль в развитии творческого мышления, я выявила возможности использования проблемных ситуаций при изучении математики, а так же предлагаю определенную систему карточек с разной степенью проблемности одного и того же задания для учащихся с различным уровнем творческого мышления. После серии уроков с использованием карточек, я провела тестирование. Обработанные результаты позволили сделать вывод о повышении уровня творческого мышления на уровне значимости (см. Приложение №1).
За прошедший межаттестационный период я получила определенные результаты в работе, но я не считаю, что достигнутый уровень как в саморазвитии, так и в педагогической деятельности является оптимальным. Поэтому в следующий м/а период я планирую:
Продолжить внедрение методики проблемного обучения на уроках русского языка, литературы, окружающего мира.
( математика)
Разработать комплекс заданий и упражнений проблемного характера по другим предметам.
Продолжать работать над решением проблемы недостатка материально-технического обеспечения путем изготовления и приобретения новых пособий;
Единственным плодотворным путем развития творческого мышления в детстве становится максимально полное раскрытие потенциальных возможностей, природных задатков, и учитель должен создать такую полноценно развивающуюся деятельность для учащихся, чтобы потенциал их не остался невостребованным.
Литература:
Артемов А.К. Приемы организации развивающего обучения//Начальная школа. - 2005. - №3.
Блохин И.А., Ляхин В.В., Стрекозин В.П. О проблемном обучении в
начальных классах//Начальная школа. – 2004. - №6.
Брушлинский А.В. Психология мышления и проблемное обучение. – М.: Знание, 2009г.
Винокурова Н. Сборник тестов и упражнений для развития ваших
способностей: Учебное пособие. – М.: ИМПЭТО, 2005г.
Гальперин П.Я. Котик Н.Р. К психологии творческого мышления//Вопросы психологии. – 1999г. - №5.
Как определить и развить способности ребенка. – СПб.: Пекспекс, 2006г.
Кудрявцев Т.В. Проблемное обучение: истоки, сущность, перспективы. –
М.: Знание, 1991г.
Лернер И.Я. Проблемное обучение. – М.: Знание, 2004г.
Оконь В. Основы проблемного обучения. – М.: Просвещение, 2003г.
Селевко Г.К. Современные образовательные технологии//Школьные
технологии. – 2007г. - №6.
Приложение №1
Приложение №1
Приложение №1
Приложение №2
Виды карточек – заданий по уровням проблемности
Высокий уровень
Закрепление табличных случаев умножения.
Продолжи ряд:
2, 4, 6, 8, …
7, 14, 21, …
8, 16, 24, …
Составь самостоятельно свой ряд.
Средний уровень
Закрепление табличных случаев умножения.
Продолжи ряд, вспомнив таблицу умножения на 2, на 7 и на 8:
2, 4, 6, 8, …
7, 14, 21, …
8, 16, 24, …
Составь свой ряд.
Низкий уровень
Закрепление табличных случаев умножения.
Вспомни таблицу умножения на 2, на 7, на 8.
Продолжи ряд чисел, как в 1 случае:
1) 2, 4, 6, 8, 10, 12, 14, 16, 18, 20;
2) 8, 16, 24, …;
3) 7, 14, 24, …
Составь свой ряд.
Очень низкий уровень
Закрепление табличных случаев умножения.
Продолжи ряд чисел, вспомнив таблицу умножения на 2, на 7, на 8 и
запиши таблицу умножения, которую использовал при выполнении задания, как в 1 случае:
1) 2, 4, 6, 8, 10, 12, 18, 20; 2*1=2 2*6=12
2) 8, 16, 24, …; 2*2=4 2*7=14
3) 7, 14, 24, … 2*3=6 2*8=16
2*4=8 2*9=18
2*5=10 2*10=20
Приложение №2
Высокий уровень
Задачи на смекалку.
Найди простой способ вычисления суммы всех чисел в ряду от 1 до 20.
Средний уровень
Задачи на смекалку.
Найди сумму такой пары чисел, чтобы можно было простым способом
произвести вычисление.
1+2+3+…+18+19+20=
Приложение №2
Низкий уровень
Задачи на смекалку.
Найди простой способ вычисления, соединив линиями пары чисел.
1+2+3+…+18+19+20=
Очень низкий уровень
Задачи на смекалку.
Найди сумму каждой пары чисел, соединенных линиями.
Вычисли простым способом сумму всех чисел.
1+2+3+…+18+19+20=
Приложение №2
Высокий уровень
Переместительное свойство сложения.
Как быстро решить эти четыре примера?
36+18+12= 24+37+16=
47+35+3= 47+38+13=
Средний уровень
Переместительное свойство сложения.
Воспользуйтесь перестановкой слагаемых и быстро решите эти примеры.
36+18+12= 24+37+16=
47+35+3= 47+38+13=
Приложение №2
Низкий уровень
Переместительное свойство сложения.
Воспользуйтесь перестановкой слагаемых и быстро решите примеры как
в 1случае.
36+18+12=36+30+66 24+37+16=
47+35+3= 47+38+13=
Очень низкий уровень
Переместительное свойство сложения.
Быстро решите примеры, вспомнив свойство сложения: от перестановки
слагаемых сумма не меняется. Сначала сложите числа, которые в сумме дают круглое число. С круглыми числами легче выполнять действие.
36+18+12=36+30+66 24+37+16=
47+35+3= 47+38+13=
Высокий уровень
Закрепление табличных случаев деления.
Продолжи ряд:
20, 18, 16, 14, …
70, 63, 56, …
80, 72, 64, …
Составь самостоятельно свой ряд.
Средний уровень
Закрепление табличных случаев деления.
Продолжи ряд, вспомнив таблицу деления на 2, на 7 и на 8:
20, 18, 16, 14, …
70, 63, 56, …
80, 72, 64, …
Составь свой ряд.
Низкий уровень
Приложение №2
Закрепление табличных случаев деления.
Вспомни таблицу деления на 2, на 7, на 8.
Продолжи ряд чисел, как в 1 случае:
1) 20, 18, 16, 14, 12, 10 , 8 , 6 , 4 , 2;
2) 70, 63, 56, …
3) 80, 72, 64, …
Составь свой ряд.
Очень низкий уровень
Закрепление табличных случаев деления.
Продолжи ряд чисел, вспомнив таблицу умножения на 2, на 7, на 8 и
запиши таблицу умножения, которую использовал при выполнении задания, как в 1 случае:
1) 20, 18, 16, 14, 12, 10 , 8 , 6 , 4 , 2; 2*1=2 2*6=12
2) 70, 63, 56, … 2*2=4 2*7=14
3) 80, 72, 64, … 2*3=6 2*8=16
2*4=8 2*9=18
2*5=10 2*10=20
Высокий уровень
Закрепление табличных случаев умножения.
Продолжи ряд:
3, 6, 9, …
6, 12, 18, …
9, 18, 27, …
Составь самостоятельно свой ряд.
Средний уровень
Закрепление табличных случаев умножения.
Продолжи ряд, вспомнив таблицу умножения на 3, на 6 и на 9:
3, 6, 9, …
6, 12, 18, …
9, 18, 27, …
Составь свой ряд.
Приложение №2
Низкий уровень
Закрепление табличных случаев умножения.
Вспомни таблицу умножения на 3, на 6, на 9.
Продолжи ряд чисел, как в 1 случае:
1) 3, 6, 9, 12, 15, 18, 21, 24, 27, 30;
2) 6, 12, 18, …;
3) 9, 18, 27, …
Составь свой ряд.
Очень низкий уровень
Закрепление табличных случаев умножения.
Продолжи ряд чисел, вспомнив таблицу умножения на 3, на 6, на 9 и
запиши таблицу умножения, которую использовал при выполнении задания, как в 1 случае:
1) 3, 6, 9, 12, 15, 18, 21, 24, 27, 30; 3*1=3 3*6=18
2) 6, 12, 18, …; 3*2=6 3*7=21
3) 9, 18, 27, … 3*3=9 3*8=24
3*4=12 3*9=27
3*5=15 3*10=30
Высокий уровень
Закрепление табличных случаев деления.
Продолжи ряд:
30, 27, 24, …
60, 54, 48, …
90, 81, 72, …
Составь самостоятельно свой ряд.
Средний уровень
Закрепление табличных случаев деления.
Продолжи ряд, вспомнив таблицу деления на 3, на 6 и на 9:
30, 27, 24, …
60, 54, 48, …
90, 81, 72, …
Составь свой ряд.
Низкий уровень Приложение №2
Закрепление табличных случаев деления.
Вспомни таблицу деления на 3, на 6, на 9.
Продолжи ряд чисел, как в 1 случае:
1) 30, 27, 24, 21, 18, 15, 12 , 9 , 6 , 3;
2) 60, 54, 48, …
3) 90, 81, 72, …
Составь свой ряд.
Очень низкий уровень
Закрепление табличных случаев деления.
Продолжи ряд чисел, вспомнив таблицу умножения на 3, на 6, на 9 и
запиши таблицу умножения, которую использовал при выполнении задания, как в 1 случае:
1) 30, 27, 24, 21, 18, 15, 12 , 9 , 6 , 3; 3*1=2 3*6=12
2) 60, 54, 48, … 3*2=4 3*7=14
3) 90, 81, 72, … 3*3=6 3*8=16
3*4=8 3*9=18
3*5=10 3*10=20
Приложение №2
Высокий уровень
Задачи на смекалку.
Найди простой способ вычисления суммы всех чисел в ряду от 1 до 20.
Средний уровень
Задачи на смекалку.
Найди сумму такой пары чисел, чтобы можно было простым способом произвести вычисление.
1+2+3+…+18+19+20=
Приложение №2
Низкий уровень
Задачи на смекалку.
Найди простой способ вычисления, соединив линиями пары чисел.
1+2+3+…+18+19+20=
Очень низкий уровень
Задачи на смекалку.
Найди сумму каждой пары чисел, соединенных линиями.
Вычисли простым способом сумму всех чисел.
1+2+3+…+18+19+20=
Приложение №2
Высокий уровень
Переместительное свойство сложения.
Как быстро решить эти четыре выражения?
36+18+12= 24+37+16=
47+35+3= 47+38+13=
Средний уровень
Переместительное свойство сложения.
Воспользуйтесь перестановкой слагаемых и быстро решите эти выражения.
36+18+12= 24+37+16=
47+35+3= 47+38+13=
Приложение №2
Низкий уровень
Переместительное свойство сложения.
Воспользуйтесь перестановкой слагаемых и быстро решите выражения как
в 1случае.
36+18+12=36+(18+12)=66 24+37+16=
47+35+3= 47+38+13=
Очень низкий уровень
Переместительное свойство сложения.
Быстро решите примеры, вспомнив свойство сложения: от перестановки
слагаемых сумма не меняется. Сначала сложите числа, которые в сумме дают круглое число. С круглыми числами легче выполнять действие.
36+18+12=36+(18+12)=36+30=66 24+37+16=
47+35+3= 47+38+13=
Высокий уровень
Переместительное свойство сложения.
Как быстро решить эти четыре выражения?
32+15+18= 23+16+37=
45+3+35= 42+13+38=
Средний уровень
Переместительное свойство сложения.
Воспользуйтесь перестановкой слагаемых и быстро решите эти выражения.
32+15+18= 23+16+37=
45+3+35= 42+13+38=
Приложение №2
Низкий уровень
Переместительное свойство сложения.
Воспользуйтесь перестановкой слагаемых и быстро решите выражения как
в 1случае.
32+15+18=15+(32+18)=65 23+16+37=
45+3+35= 42+13+38=
Очень низкий уровень
Переместительное свойство сложения.
Быстро решите примеры, вспомнив свойство сложения: от перестановки
слагаемых сумма не меняется. Сначала сложите числа, которые в сумме дают круглое число. С круглыми числами легче выполнять действие.
32+15+18=15+(32+18) = 15+50=65 23+16+37=
45+3+35= 42+13+38=
Высокий уровень
Усвоение смысла умножения.
Замени сложение умножением:
1+1+1+1+1=
7+7+7=
0+0+0+0=
7+1+0=
9+9+9+9+9+9=
Средний уровень
Усвоение смысла умножения.
Замени сложение умножением. Чем отличается четвертое выражение от остальных?
1+1+1+1+1=
7+7+7=
0+0+0+0=
7+1+0=
9+9+9+9+9+9=
Приложение №2
Низкий уровень
Усвоение смысла умножения.
Замени сложение умножением, вспомнив, что называется умножением.
1+1+1+1+1=
7+7+7=
0+0+0+0=
7+0+1=
9+9+9+9+9+9=
Чем отличается 4 выражение от остальных?
Очень низкий уровень
Усвоение смысла умножения.
Замени сложение умножением, вспомнив, что сложение только слагаемых
можно назвать умножением.
1+1+1+1+1=
7+7+7=
0+0+0+0=
1+7+0=
9+9+9+9+9+9=
Чем отличается 4 выражение от остальных?
Высокий уровень Приложение №2
Распределительный закон умножения относительно сложения.
Реши простым способом выражения и придумай похожие.
597*10-(597*8+597*2)=
793-(703*96-703*96)=
(97*8+97*2)-900=
Средний уровень
Распределительный закон умножения относительно сложения.
Реши выражения простым способом.
597*10-(597*8+597*2)=
793-(703*96-703*96)=
(97*8+97*2)-900=
Низкий уровень
Распределительный закон умножения относительно сложения.
Реши выражения, используя свойство умножения относительно сложения.
597*10-(597*8+597*2)=
793-(703*96-703*96)=
(97*8+97*2)-900=
Очень низкий уровень
Распределительный закон умножения относительно сложения.
Решите выражения, используя свойство умножения относительно сложения: а(b+c)=a*b+a*c
597*10-(597*8+597*2)=
793-(703*97-703*96)=
(97*8+97*2)-900=
Высокий уровень Приложение №2
Решение неравенств.
Реши неравенство без вычисления.
8304-6209 … 8304-7000
Средний уровень
Решение неравенств.
Решите неравенство без вычисления (используя чертеж).
8304-6209 … 8304-7000
Низкий уровень
Решение неравенств.
Реши неравенство без вычисления, сравнив:
8304-6209 … 8304-7000
6209… 7000
Очень низкий уровень
Решение неравенств.
Реши неравенство без вычисления, проговаривая:
если 6209… 7000, а вычитая из одного и того же числа меньшее число, мы получаем…, значит:
8304-6209 … 8304-7000
Приложение №2
Высокий уровень
Доли.
Реши задачу:
Пассажир, проехав третью часть пути, заснул. Когда он проснулся, ему осталось ехать еще половину того пути, что он проехал спящим. Какую часть всего пути он проспал?
Средний уровень
Доли.
Реши задачу, сделав рисунок:
Пассажир, проехав третью часть пути, заснул. Когда он проснулся, ему осталось ехать еще половину того пути, что он проехал спящим. Какую часть всего пути он проспал?
Низкий уровень
Доли.
Посмотри внимательно на рисунок и реши задачу:
проспал
Пассажир, проехав третью часть пути, заснул. Когда он проснулся, ему осталось ехать еще половину того пути, что он проехал спящим. Какую часть всего пути он проспал?





![]()
Очень низкий уровень
Доли.
Дана задача и рисунок к ней.
проспал
Пассажир, проехав третью часть пути, заснул. Когда он проснулся, ему осталось ехать еще половину того пути, что он проехал спящим. Какую часть всего пути он проспал?
На сколько частей разделен весь путь?
Объясни почему и найди ответ на вопрос задачи.





Высокий уровень
Продолжи числовой ряд:
25, 19, 39, 33, 43…
36, 37, 30, 31…
46, 26, 56…
Средний уровень
Продолжи числовой ряд, обрати внимание на «соседей» числа:
1)25, 19, 39, 33, 43…
2)36, 37, 30, 31…
3)46, 26, 56…
Низкий уровень
Продолжи числовой ряд, как в 1 случае:
1)25, 19, 39, 33, 43, 37, 47, 41, 51, 45.
2)36, 37, 30, 31…
3)46, 26, 56…
![]()
Очень низкий уровень
Продолжи числовой ряд, как в 1 случае. Как изменилось 2 число по отношению к первому, как 3 число по отношению ко 2…
1)25, 19, 39, 33, 43, 37, 47, 41, 51, 45.
2)36, 37, 30, 31…
3)46, 26, 56…
Приложение №2
Высокий уровень
Продолжи числовой ряд:
1)525, 519, 539, 533, 543…
2)136, 137, 130, 131…
3)746, 726, 756…
Средний уровень
Продолжи числовой ряд, обрати внимание на «соседей» числа:
1)525, 519, 539, 533, 543…
2)136, 137, 130, 131…
3)746, 726, 756…
Низкий уровень
Продолжи числовой ряд, как в 1 случае:
1)525, 519, 539, 533, 543, 537, 547, 541, 551, 545.
2)136, 137, 130, 131…
3)746, 726, 756…
![]()
Очень низкий уровень
Продолжи числовой ряд, как в 1 случае. Как изменилось 2 число по отношению к первому, как 3 число по отношению ко 2…
1)525, 519, 539, 533, 543, 537, 547, 541, 551, 545.
2)136, 137, 130, 131…
3)746, 726, 756…
Приложение №2
Высокий уровень
В классе было 20 учеников, в течение учебного года 4 ученика перешли в другую школу. За это время поступили 2 новых ученика.
Средний уровень
В классе было 20 учеников, в течение учебного года 4 ученика перешли в другую школу. За это время поступили 2 новых ученика. Поставь вопрос и реши задачу.
Низкий уровень
В классе было 20 учеников, в течение учебного года 4 ученика перешли в другую школу. За это время поступили 2 новых ученика. Сколько учеников в классе?
![]()
Очень низкий уровень
В классе было 20 учеников, в течение учебного года 4 ученика перешли в другую школу. За это время поступили 2 новых ученика. Сколько учеников в классе?
Было – 20 учеников.
Перешли – 4 ученика. Сколько всего ?
Поступили – 2 ученика.
Высокий уровень
За границу отравляются туристы: на самолете – 35 человек, на поезде на 35 больше чем на самолете, а на автобусе на 22 меньше чем на поезде.
Средний уровень
За границу отравляются туристы: на самолете – 35 человек, на поезде на 35 больше чем на самолете, а на автобусе на 22 меньше чем на поезде.
Поставь вопрос и реши задачу.
Низкий уровень
За границу отравляются туристы: на самолете – 35 человек, на поезде на 35 больше чем на самолете, а на автобусе на 22 меньше чем на поезде.
Сколько человек поедут на автобусе?
![]()
Очень низкий уровень
За границу отравляются туристы: на самолете – 35 человек, на поезде на 35 больше чем на самолете, а на автобусе на 22 меньше чем на поезде.
Сколько человек поедут на автобусе?
С. – 35
А. – на 35 б. 
П. – на 22 м. - ?

Высокий уровень
Занимательные рамки
Средний уровень
Занимательные рамки, сумма чисел равна 90.
Низкий уровень
Занимательные рамки, найди сумму чисел по вертикали и горизонтали и вычти из 90.
![]()
Очень низкий уровень
Занимательные рамки, найди сумму чисел по вертикали и горизонтали и вычти из 90.
Составь выражения.
Высокий уровень
Реши задачу:
Коля поймал 10 рыбок - Саша 12 рыбок , а Петя – на 3 рыбки меньше, чем Коля. Сколько рыбок поймал Петя?
Какой возник вопрос?
Средний уровень
Реши задачу, :
Коля поймал 10 рыбок - Саша 12 рыбок , а Петя – на 3 рыбки меньше, чем Коля. Сколько рыбок поймал Петя?
Кто из мальчиков в задаче лишний?
Какой возник вопрос?
Низкий уровень
Реши задачу, :
Коля поймал 10 рыбок - Саша 12 рыбок , а Петя – на 3 рыбки меньше, чем Коля. Сколько рыбок поймал Петя?
О каком мальчике мы не упомянули?
Кто из мальчиков в задаче лишний?Почему?
Какой возник вопрос?
![]()
Очень низкий уровень
Реши задачу, :
Коля поймал 10 рыбок - Саша 12 рыбок , а Петя – на 3 рыбки меньше, чем Коля. Сколько рыбок поймал Петя?
Сколько рыбок поймал Коля?
Сколько рыбок поймал Петя?
О каком мальчике мы не упомянули?
Кто из мальчиков в задаче лишний?Почему?
Какой возник вопрос?
Приложение №4
Фрагмент урока математики во 2 классе (1-3).
Тема: Порядок действий в выражениях со скобками.
| Этап урока |Деятельность учителя |Деятельность ученика |
| | | |
| Изучение нового |Ученик у доски получил два | |
| материала |задания: «К 2 прибавь 5 и | |
| |помножь на 3» и другое: «К 2 | |
| |прибавь 5, помноженное на 3». |Он записал и вычислил следующим |
| |Учитель подводит школьников к |образом: |
| |противоречию и предлагает им |2+5*3=21 |
| |самим найти способ его |2+5*3=17 |
| |разрешения: | |
| |Почему при одинаковой записи | |
| |примеров у нас получились разные|Учащиеся высказывают возможные |
| |результаты? |варианты решения этой проблемы: |
| | |оба результата правильны, они |
| | |зависят от того, в какой |
| | |последовательности выполняется |
| | |сложение и умножение. |
| |Какое действие (сложение или |В первом примере сначала |
| |умножение) выполнено первым, |выполнили сложение, потом |
| |какое – вторым в этих примерах? |умножение. Во втором – сначала |
| | |умножение, затем сложение. |
| |Возникает проблемный вопрос: Как|Учащиеся побуждаются к поиску |
| |записать этот пример, чтобы |решения проблемы и приходят к |
| |получить правильный ответ? |понятию скобок: Нужно расставить|
| | |скобки: |
| | |(2+5)*3=21 |
| |Кто сформулирует правило порядка|2+(5*3) |
| |скобками? |вычисляют значение выражения в |
| |Повторите, какое правило мы |скобках. |
| |вывели. Пропустите правило в |Учащиеся проверяют «свое» |
| |своей формулировке. |правило, уточняют его, |
| | |совершенствуют. |
| |В учебнике это правило дано в |Учащиеся сравнивают «свое» |
| |таком виде: Если в выражении |правило с правилом в учебнике. |
| |есть скобки, то сначала | |
| |выполняют значение выражения в | |
| |скобках. В полученном выражении | |
| |выполняют по порядку слева | |
| |направо сначала умножение и | |
| |деление, а потом сложение и | |
| |вычитание. | |
| |Учитель сообщает тему урока: |Учащиеся сами подошли к тому, |
| |сегодняшняя тема урока – порядок|что будут изучать на данном |
| |действий в выражениях со |уроке. |
| |скобками. | |
Приложение №3
Тематический план факультатива по математике. 3 класс.
|Месяц |Тема |
|Сентябрь-октябрь |Сложение и вычитание в пределах 100.|
| |Развитие восприятия и воображения. |
|Ноябрь-декабрь |Умножение и деление в пределах 100. |
| |Развитие легкости и точности |
| |мышления. |
|Январь-февраль |Закрепление табличных случаев |
| |умножения и деления. Развитие |
| |гибкости мыслительных процессов. |
|Март-апрель |Развитие оригинальности |
| |мышления. |
|Май |Простые и составные задачи. Развитие
| |творческого мышления. |
Занятие факультатива по математике (2 класс, I четверть)
Тема занятия: Сложение и вычитание в пределах 100.
Развитие восприятия и воображения.
Цель.
1) Закрепить навыки сложения и вычитания в пределах 100.
2) Развивать и совершенствовать воображение учащихся.
Оборудование: классная доска, плакаты с заданиями, набор спичек
у каждого учащегося, карточки для игры «Внимание».
Ход занятия:
- Сегодня мы проведем первый факультатив по математике. Но
Чтобы запомнить все, что увидим, надо быть очень внимательным. Поэтому перед началом нашей работы мы потренируем наше внимание.
I. Игра «Внимание»: учитель показывает карточку с изображением какой-либо фигуры, ученики должны запомнить то, что было на карточке, и зарисовать это в своей тетради «Творчество».
Карточка находится перед глазами учеников не более 2-3 с. За одну игру учитель показывает не более 6-8 карточек (размером 7х9 см).
II. Разминка для ума.
1. Даны числа:
23 74 41 14
40 17 60 50
Какое число меньшее в каждой строке? (в первой строке лишнее число 74,
у остальных чисел сумма цифр равна 5; во второй – 17, в записи остальных чисел есть 0).
2. Что общего в записи чисел каждой строки:
12 24 20 22
30 37 13 83
(в записи чисел первой строки использована цифра 2,а во второй–цифра 3).
3. По какому правилу записан каждый ряд чисел?
Продолжи его:
10 30 50 …
14 34 54 …
(числа в первой и во второй строке записаны через 20)
4. По какому признаку записаны столбики примеров:
27+5 76+20 44+2
39+5 56+30 34+5
29+4 35+40 32+6
(основу классификации составляет вычислительный прием)
5. Чем похожи между собой записанные в каждом столбике примеры и чем
отличаются?
60-6 32-11
60-16 32-13
6. Придумай к каждому данному примеру похожий пример:
12+6=18
16-4=12
(при составлении таких примеров учащихся должны указать тот признак,
на который они ориентируются).
7. Найди ошибки и исправь решение примеров:
43-11=43-(10+1)=33+1=34
60-17=60-(10+7)=50+7=57
III. Задания со спичками.
Отсчитайте 12 спичек и выложите их по образцу рисунка.
Переложите 8 спичек так, чтобы получилось 4 равных квадрата. Нарисуйте их в тетрадь. Верните все спички в исходное положение. Теперь переложите 8 спичек так, чтобы получилась мельница; нарисуй ее в тетради.
IV. Цифровой диктант.
Если вы согласны с утверждениями, высказанными мною, поставьте цифру 1, если вы считаете, что информация неправильная – ставьте 0. в конце диктанта дайте итоговый ответ. Работу нужно выполнить в быстром темпе.
1) 36+3-6=33
2) моя любимая сказка «Али-Баба и 20 разбойников»
3) 55+53=98
4) май в году по счету пятый
5) букв в русском алфавите 33
6) 100-20+1=91
7) чертова дюжина – это 13.
Итог: 4
Ответ: 1 – 0 – 0 – 1 – 1 – 0 – 1
Домашнее задание:
Раздели числа на две группы: 15, 24, 25, 28, 30, 32, 35, 36, 40.
Итог: вот и закончилось наше занятие! Понравилось? Встретимся через месяц. Кто придумает интересное задание и продемонстрирует на следующем факультативе, я буду благодарна и рада.
I. Задачи с меняющимся содержанием.
1) Ворон живет около 75 лет, слон на 5 лет меньше, а щука на 5 лет меньше, чем слон. На сколько лет меньше живет щука чем ворон? (2-й вариант: на сколько лет меньше живет щука, чем слон?)
2) Брат и сестра читают книгу «Маугли», в которой 60 страниц. Брат читает каждый день по 15 страниц, а сестра по 20. кто из них раньше прочитает всю книгу? (2-й вариант: слово «раньше» заменяется словом «позже»).
3) На озеро прилетело 48 уток и 6 гусей. Во сколько раз уток больше чем гусей? (2-й вариант: на сколько уток больше чем гусей).
4) Кате 10 лет, а Свете в 2 раза меньше. Алена в 3 раза старше Светы. Сколько лет Свете и Алене? (2-й вариант: Света на 2 года младше, а Алена на 3 года старше Светы).
5) На 3 теплицы потребовалось 60 м пленки. Сколько пленки нужно для 6 таких теплиц? (2-й вариант: на 6 теплиц потребовалось 60 м пленки, сколько пленки нужно для 3 таких теплиц?).
II. Задачи на перестройку действия.
1) Замени сложение умножением:
4+4+4=
6+6+6+6+6=
2+2=
9+9+9+9=
5+5+5+5+5+5+5=
а+а+а=
3+2+5=
2) Дано 4, прибавь 3, потом умножь на 3;
дано 1
дано 5
дано 14
дано 31
дано 47
дано х
дано а
дано 2а
дано 3а, раздели на 3, потом вычти 3.
3) Периметр квадрата равен 16. Какой станет пример этой фигуры, если:
1. Его стороны уменьшить вдвое;
2. Его стороны уменьшить на 1 см;
3. Его стороны уменьшить на 3 см;
4. Его стороны увеличить втрое.
4) Специальный тест.
|137 |795 |421 |317 |651 |
|349 |274 |953 |017 |273 |
|654 |034 |219 |526 |398 |
|703 |721 |615 |130 |731 |
|275 |392 |543 |754 |210 |
|372 |908 |043 |420 |539 |
Этот тест представляет собой своего рода корректурную таблицу. Учащимся дается задание зачеркнуть все сочетания цифр, где имеется цифра 3.
Задание предлагается выполнить возможно быстрее. После этого дается второй экземпляр такой же таблицы с противоположным заданием – зачеркнуть все числа, кроме тех, где есть цифра 3.
Отмечается время, затраченное на выполнение каждого задания, и количество ошибок. Задание совершенно равноценны в отношении трудностей: в таблице имеется 15 чисел с цифрой 3 и столько же без этой цифры.
III. Задачи, наталкивающие на «самоограничение».
1) дано 9 точек.
Соедините их одной непрерывной ломаной линией из четырех отрезков (не отрывая карандаша от бумаги).
2) Маше и Ксюше вместе 10 лет, четыре года назад было 2 года. Сколько
лет Маше и Ксюше, если Маша старше Ксюши на 2 года?
3) Из пяти палочек постройте 2 треугольника.
4) Одним отрезком прямой пересечь четырехугольник, чтобы получилось 2 треугольника.
IV. Задачи с несколькими решениями.
1) В два автобуса сели 123 экскурсанта, затем из одного вышло 8 человек, трое из них село во второй автобус. После этого стало пассажиров поровну. Сколько пассажиров было в каждом автобусе вначале? (67 чел и 56 чел).
2) В древнехакасской армии (IX век) насчитывалось несколько тысяч воинов, а у их врагов – уйгуров в 2 раза больше. Вместе у них было 90 тысяч воинов. Сколько солдат в каждой армии. (30 тыс и 60 тыс).
3) В столовую привезли 4 мешка сахара и 6 мешков муки, всего 500 кг.
Причем вместимость мешков была одинаковая. Найдите сколько кг муки и кг сахара привезли в столовую? (200 и 300)
4) Для озеленения города было закуплено 200 штук кленов за 360 рублей
и 300 лип, стоимость которых в 2 раза больше. Сколько заплатили за клены и липы всего? (288.000)
5) Рабочему поручено изготовить за 10 часов – 30 деталей. Но он
экономил время, успевая делать 1 деталь за 15 минут. Сколько деталей сверх задания сделает рабочий за счет сэкономленного времени? (10 дет.)
6) Одна половина участка занята огородом, другая – садом и цветником.
Сад занимает 400 м2, цветник [pic] этой площадки. Чему равна площадь всего участка? (840 м2).
V. Задачи на соображение, логическое рассуждение.
1) Летела стая гусей: один гусь впереди, а два позади; один позади, а два впереди; один гусь между двумя и три в ряд. Сколько было всего гусей? (3 гуся, изобразить из по-разному).
2)По двору ходят куры и кролики, у всех вместе 20 голов и 52 ноги. Сколько всего кур и кроликов во дворе? (6 кроликов и 14 кур).
3) Сын спросил у отца, сколько ему лет. Отец ответил: «Если к моим годам прибавить полсотни и еще 5 лет, то мне будет 100 лет». Сколько лет отцу? (45 лет).
4) Лестница состоит из 15 ступеней. На какую ступеньку надо встать, чтобы быть на середине лестницы? (на восьмую).
5) На уроке физкультуры ученики выстраивались в линейку на расстоянии 1 м друг от друга. Вся линейка растянулась на 25 м. Сколько было учеников? (26 учеников).
6) Миша захотел узнать, сколько лет его дедушке. Дедушка ответил: «Догадайся сам. Если из наибольшего двузначного числа вычесть 90, результат увеличить в три раза и прибавить 73, то получится число моих лет». Сколько лет дедушке? (100 лет).
7) В древнехакасском государстве тархан (вельможа) младше цзян-цзеня (генерала), а цзян-цзюн младше кагана (государя). Кто младше, тархан или каган?
VI. Задачи типа: «Продолжи ряд».
1) Числовой тест.
2, 4, 6, 8, …
3, 6, 12, …
4, 9, 16, 25, …
20, 18, 16, 14, …
2, 3, 4, 9, 16, …
1, 4, 16, 64, …
5, 10, 15, 20, …
11, 13, 15, 17, …
9, 10, 11, 12, …
81, 27, 9, …
2) Фигурный текст.
1. Какая геометрическая фигура здесь лишняя?
2. Слева четыре фигуры, образующие ряд. Справа пять фигур. Найди среди них ту, которая подходит в левый ряд пятой.
3) Найди фигуру в правой части, которая так относилась бы к третьей
фигуре, слева, как вторая относится к первой.
4) Какой фигуры недостает?
VII. Задачи на доказательство.
1) Восстанови пропущенные цифры в записи сложения:
*54 *2* 5*6
1*4 2*3 *5*
468 997 690
2) Восстанови пропущенные цифры в записи вычитания:
*9* 7*8 *2*
1*3 *2* 1*3
271 584 369
3) Восстанови пропущенные цифры в записи умножения и деления:
4*0:2=220
9**:3=300
28x*=84
*9:3=13
9*:15=6
22x1*=264
4) Восстанови пропущенные цифры в записи умножения:
3* *4 ** 9*
* * 5 *
**7 4*6 8* *76
5) Найди цифровое значение букв в этой условной записи сложения и умножения:
авж бё
да е
ажз аеб
VIII. Задачи с различной степенью наглядности решения.
1) Пассажир, проехав третью часть пути, заснул. Когда он проснулся, ему осталось ехать еще половину того пути, что он проехал спящим. Какую часть всего пути он проспал?
2) Сколько весит кирпич, если он весит один килограмм плюс полкирпича? (2 кг).
3) Банка с керосином весит 8 кг. Из нее вылили половину керосина, после чего банка стала весить 4,5 кг. Определить вес банки (1 кг).
4) Два грузовика в одно время выехали из пункта А в пункт Б и обратно (без остановки). Первый грузовик двигался все время с одной и той же скоростью вдвое меньшей, чем первый, но зато обратно со скоростью вдвое большей, чем первый. Какой грузовик раньше вернется в пункт А? (оба вернутся в одно и тоже время).
5) Дочери 8 лет, матери 38 лет. Через сколько лет мать будет втрое старше дочери? (через 7 лет).
6) Каковы должны быть размеры квадрата, чтобы его пример численно равняется его площади? (4).
7) Высота сосны 20 метров. По ней ползет улитка. Каждый день поднимается на 2 метра вверх и каждую ночь спускаясь на 1 м вниз. За сколько дней улитка поднимется на вершину сосны?
Высокий уровень
| х | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| у | 1 | 4 | 9 | 16 | 25 |
|
|
|
|
Средний уровень
Умножение.
Проанализируйте зависимость между переменными х и у.
| х | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| у | 1 | 4 | 9 | 16 | 25 |
|
|
|
|
Приложение №2
Низкий уровень
Усвоение смысла умножения.
Проанализируйте зависимость между переменными х и у, назовите формулы.
| х | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| у | 1 | 4 | 9 | 16 | 25 |
|
|
|
|
Очень низкий уровень
Умножение.
Проанализируйте зависимость между переменными х и у. Во сколько раз увеличилось число 2? 3? Во сколько раз нужно увеличилось 6?
| х | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| у | 1 | 4 | 9 | 16 | 25 |
|
|
|
|
Высокий уровень
| х | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| у | 3 | 6 | 11 | 18 | 27 | 38 |
|
|
|
Средний уровень
Умножение.
Проанализируйте зависимость между переменными х и у.
| х | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| у | 1 | 4 | 9 | 16 | 25 |
|
|
|
|
Приложение №2
Низкий уровень
Усвоение смысла умножения.
Проанализируйте зависимость между переменными х и у, назовите формулы.
| х | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| у | 1 | 4 | 9 | 16 | 25 |
|
|
|
|
Очень низкий уровень
Умножение.
Проанализируйте зависимость между переменными х и у. Во сколько раз увеличилось число 2? 3? Во сколько раз нужно увеличилось 6?
| х | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| у | 1 | 4 | 9 | 16 | 25 |
|
|
|
|



 Получите свидетельство
Получите свидетельство Вход
Вход






















 Материал по математике по теме "Использование проблемных ситуаций на уроках математики в развитии творческого мышления младших школьников" (1.11 MB)
Материал по математике по теме "Использование проблемных ситуаций на уроках математики в развитии творческого мышления младших школьников" (1.11 MB)
 0
0 2377
2377 65
65 Нравится
0
Нравится
0


