Материал по математике «Формирование универсальных учебных действий у обучающихся 9 классов в процессе решения задач по теме «Проценты»»

Учитель

Зенина О.П.

Класс

9 класс

Раздел

Системы уравнений как математические модели реальных ситуаций

Результаты

обучения

по разделу

Личностные

Метапредметные

Предметные

Умение ясно, точно, грамотно излагать свои мысли в устной и письменной речи, понимать смысл поставленной задачи;

умение контролировать процесс и результат учебной математической деятельности; развивать критичность мышления;

умение выделить нравственный аспект поведения и соотнести поступки и события с принятыми этическими принципами.

Умение видеть математическую задачу в контексте проблемной ситуации в окружающей жизни;

умение находить в различных источниках информацию, необходимую для решения математических проблем;

умение самостоятельно ставить цели, выбирать и создавать алгоритмы для решения учебных математических проблем;

умение планировать и осуществлять деятельность, направленную на решение задач исследовательского характера.

Понимать и использовать в речи терминологию: отыскание процента от числа, числа по его проценту, процентное содержания одного числа от другого.

Уметь переводить проценты в десятичную дробь, обыкновенные и десятичные дроби в проценты. Решать основные задачи на проценты, в том числе задачи с практическим содержанием. Применять различные способы решения основных задач на проценты.

Приводить примеры задач на нахождение процента от числа, числа по его проценту, процентного содержания одного числа от другого.

Обнаруживать и уст­ранять ошибки логи­ческого (в ходе реше­ния) и арифметиче­ского (в вычислении) характера; самостоя­тельно выбирать способ решения задачи.

Анализировать и осмысливать текст задач, аргументировать и презентовать решения.

Система задач

Олимпиадные

Практико-ориентированные

Творческие

исследовательские

1. Саша за весну похудел на 20%, за лето поправился на 30%, за осень похудел на 20%, за зиму поправился на 10%. Как изменился его вес?

1. Вкладчик открыл счет в банке, внеся 2000 р. На вклад, годовой доход по которому составит 12%, и решил в течении 6 лет не брать процентные начисления. Какая сумма будет лежать на его счете через 6 лет?

1. М.В.Ломоносов тратил одну денежку на хлеб и квас. Когда цены выросли на 20%, на ту же денежку он приобретал полхлеба и квас. Хватит ли той же денежки хотя бы на квас, если цены вырастут еще на 20%?

2. Имеются два слитка золота с серебром. Процентное содержание золота в первом слитке в 2,5 раза больше, чем процентное содержание золота во втором слитке. Если сплавить оба слитка вместе, то получится слиток, в котором будет 40% золота. Найдите, во сколько раз первый слиток тяжелее второго, если известно, что при сплаве равных по весу частей первого и второго слитков получается сплав, в котором 35% золота.

2. Занятия ребенка в танцевальном кружке родители оплачивают в сбербанке, внося ежемесячно 350 р. Оплата должна производиться до 15 числа каждого месяца, после чего за каждый просроченный день начисляется пеня в размере 5 % от суммы оплаты занятий за один месяц. Сколько придется заплатить родителям, если они просрочат оплату на две недели.

2. Богатый сенатор, умирая, оставил жену в ожидании ребёнка. После смерти сенатора выяснилось, что на своё имущество, равное 350 талантам, он оставил следующее завещание: «В случае рождения сына отдать мальчику 60% состояния, 30% – матери, 10% – отдать в больницу, где родился сын; в случае же рождения дочери отдать девочке 30% состояния, матери – 60%, в больницу, в которой родилась дочь – 10%» У вдовы родились близнецы – мальчик и девочка. Такой возможности завещатель не предусмотрел. Как можно разделить имущество между тремя наследниками с наилучшим приближением к условию завещания?

1. Посевной участок под рожь имеет прямоугольную форму. В рамках реструктуризации колхозных земель одну сторону участка увеличили на 20%, а другую уменьшили на 20%. Изменится ли в результате урожай ржи, и если изменится, то на сколько?

3. Владелец дискотеки имел стабильный доход. В погоне за прибылью он увеличил цену билета на 25%. Количество посетителей резко уменьшилось, и он стал нести убытки. Тогда он вернулся к первоначальной цене билетов. На сколько процентов владелец дискотеки снизил новую цену билетов, чтобы она стала первоначальной?

3. Некто узнал о трёх изобретениях: одно из них экономит 30% топлива, другое – 45%, третье – 25%. Этот человек решил применить все три изобретения сразу, предполагая сэкономить

30% + 45% + 25% = 100% топлива.

Но разве это так? Сколько процентов экономии он получит на самом деле?

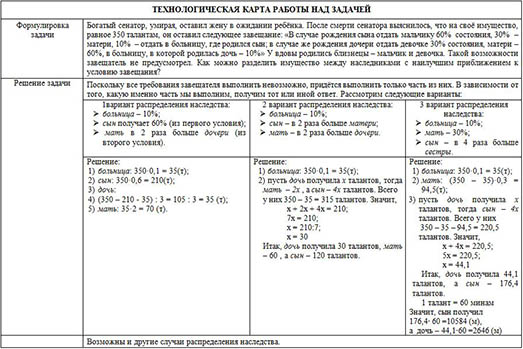
ТЕХНОЛОГИЧЕСКАЯ КАРТА РАБОТЫ НАД ЗАДАЧЕЙ

Формулировка задачи

Богатый сенатор, умирая, оставил жену в ожидании ребёнка. После смерти сенатора выяснилось, что на своё имущество, равное 350 талантам, он оставил следующее завещание: «В случае рождения сына отдать мальчику 60% состояния, 30% – матери, 10% – отдать в больницу, где родился сын; в случае же рождения дочери отдать девочке 30% состояния, матери – 60%, в больницу, в которой родилась дочь – 10%» У вдовы родились близнецы – мальчик и девочка. Такой возможности завещатель не предусмотрел. Как можно разделить имущество между наследниками с наилучшим приближением к условию завещания?

Решение задачи

Поскольку все требования завещателя выполнить невозможно, придётся выполнить только часть из них. В зависимости от того, какую именно часть мы выполним, получим тот или иной ответ. Рассмотрим следующие варианты:

1вариант распределения наследства:

• больница – 10%;

• сын получает 60% (из первого условия);

• мать в 2 раза больше дочери (из второго условия).

2 вариант распределения наследства:

• больница – 10%;

• сын – в 2 раза больше матери;

• мать – в 2 раза больше дочери.

3 вариант распределения наследства:

• больница – 10%;

• мать – 30%;

• сын – в 4 раза больше сестры.

Решение:

1. больница: 350·0,1 = 35(т);

2. сын: 350·0,6 = 210(т);

3. дочь:

4. (350 – 210 - 35) : 3 = 105 : 3 = 35 (т);

5. мать: 35·2 = 70 (т).

Решение:

1. больница: 350·0,1 = 35(т);

2. пусть дочь получила х талантов, тогда

мать – 2х , а сын – 4х талантов. Всего у них 350 – 35 = 315 талантов. Значит,

х + 2х + 4х = 210;

7х = 210;

х = 210:7;

х = 30

Итак, дочь получила 30 талантов, мать – 60 , а сын – 120 талантов.

Решение:

1. больница: 350·0,1 = 35(т);

2. мать: (350 – 35)·0,3 = 94,5(т);

1. пусть дочь получила х талантов, тогда сын – 4х талантов. Всего у них

350 – 35 – 94,5 = 220,5 талантов. Значит,

х + 4х = 220,5;

5х = 220,5;

х = 44,1

Итак, дочь получила 44,1 талантов, а сын – 176,4 талантов.

1 талант = 60 минам

Значит, сын получил

176,4∙ 60 =10584 (м),

а дочь – 44,1∙60 =2646 (м)

Возможны и другие случаи распределения наследства.

Основные этапы работы над задачей.

Цель этапа

Содержание педагогического взаимодействия

Деятельность

учителя

Деятельность обучающихся

Познавательная

Коммуникативная

Регулятивная

1. Постановка учебной задачи

Создание проблемной ситуации

1. Раздаёт текст задачи каждому ученику для анализа условия и предлагает поработать с текстом задачи.

2. Дает инструктаж к чтению текста: карандашом ставим пометки

• «+» – новая информация;

• «?» – непонятная информация.

3. Разделить текст на 3 смысловых абзаца, составить номинативный план;

4. Составите вопросы к двум последним абзацам.

1. Индивидуальная работа с текстом.

2. Новая информация «талант».

3. План:

• сенатор;

• завещание;

• распределение наследства;

4. Что получат наследники в каждом из трех рассмотренных случаях?

Слушают учителя; фронтально высказывают свою позицию;

на первый и второй пункт плана могут дать пояснения;

третий вопрос плана создает проблемную ситуацию

Понимают важность анализа условия; принимают учебную цель и формулируют проблему.

1. Исследование проблемы

Найти возможные варианты решения проблемной ситуации

1. Предлагает обучающимся поставить себя на место судьи и обсудить возможные варианты.

2. Фиксирует гипотезы.

Выдвигают возможные гипотезы фронтально:

• приоритет сыну;

• приоритет сравнению;

• приоритет матери.

• другие варианты.

Выражают свои мысли по поводу выдвинутой гипотезы, обосновывают её право на существование.

Планируют и прогнозируют своё исследование

1. Моделирование

Создать модель для решения

1. Предлагает каждому принять одну из гипотез, которая ему кажется самой подходящей

Разбиваются на группы по предпочтениям

Учебное сотрудничество; умение выражать свои мысли

Планируют свою работу

1. Поиск способа решения

Выбор способа решения

1. Предлагает установить тип задачи.

2. Какие правила могут нам пригодиться для решения задачи?

3. Какую модель можно использовать?

Каждая группа намечает план решения своей задачи

Владение

монологической и диалогической формами речи.

Выбор эффективного способа решения задачи

5. Решение задачи

Решить и записать решение.

1. Предлагает решить задачу и записать своё решение в тетради.

2. Подготовиться на доске представителю от каждой группы для представления своего решения.

1. Каждая группа сообща решает свою задачу и оформляет её.

2. Готовит своего представителя для выступления.

Умение выражать свои мысли аргументировать ответы.

Контроль и коррекция внутри группы.

6.Интерпритация полученных результатов

Анализ и оценка полученного ответа

1. Предлагает проанализировать полученные результаты.

2. Проясняет, что так как в третьем случае ответ не целое число, то возможно округление по законам математики или перевод в более мелкие денежные единицы: таланты в мины.

3. Предлагает провести сравнение результатов и попытаться найти решение с наилучшим приближением к условию завещания и обосновать его;

4. Просит обучающихся ответить на вопрос: «Как вы думаете, какой вариант из предложенных имел место быть в реальной истории и

почему?»

1.Выступление представителя каждой группы.

2.Обсуждение.

3.Выработка критериев сравнения:

• сколько условий завещания учтено;

• ответы;

• нравственный аспект.

Умение находиться в режиме активного слушания.

Разрешение конфликтных ситуаций.

Контроль, коррекция, оценка

ИНСТРУМЕНТАРИЙ ОЦЕНКИ СФОРМИРОВАННОСТИ

УНИВЕРСАЛЬНЫХ УЧЕБНЫХ ДЕЙТВИЙ (на примере двух задач)

Задание

Деятельность учащегося *

Познавательная

Коммуникативная

Регулятивная

1. Представьте, что похожая ситуация происходит в наши дни. Как распределить наследство? (задачи нет есть ситуация)

Ученик должен понимать, что возникают проблемы:

1. Будет ли вообще рассматриваться завещание, где не предусмотрен данный случай?

2. Нужно знать законы или обратиться к помощи специалистов.

3 Задача не может быть решена без дополнительной информации.

Умеет точно и ясно выражать и аргументировать свои мысли.

Умеет составить план действий по добыче информации:

1. Спрошу у родителей или знакомого юриста.

2. Поручу узнать родителям.

3. Найду информацию в интернете

Решает задачу.

1. Некто узнал о трёх изобретениях: одно из них экономит 30% топлива, другое – 45%, третье – 25%. Этот человек решил применить все три изобретения сразу, предполагая сэкономить

30% + 45% + 25% = 100% топлива. Сколько процентов экономии он получит на самом деле?

1.Постановка проблемы:

• можно ли получить 100% экономии топлива?

• как получить процент экономии?

• актуальность этой темы в свете экологических проблем.

2. Проанализировав условие понимают, что важным условием является тот факт, что эффективность каждого не зависит от применения другого. Так как если эта зависимость есть, то процент будет другим.

3. Самостоятельное решение

1. Обучающийся должен уметь объяснить почему нельзя получить 100% экономии (энергия не может возникнуть «из ничего», машина без бензина не поедет).

2. Обучающийся проводит цепочку рассуждений по анализу решения.

1. Самостоятельно поставил цель.

2. Составил план решения.

3. Решил задачу.

Критерии

Соответствует

Соответствует

частично

Не
соответствует

1. Система задач по разделу включает:

• не менее 3-х олимпиадных задач;

• не менее 3-х практико-ориентированных задач;

• не менее 3-х творческих /исследовательских задач.

2

2

2

1

1

1

0

0

0

1. По предлагаемому разделу сформулированы результаты обучения:

• личностные;

• метапредметные;

• предметные.

2

2

2

1

1

1

0

0

0

1. Представленная технологическая карта работы над задачей содержит:

• обоснованное решение задачи;

• основные этапы работы над задачей в соответствии с компонентами универсальных учебных действий.

2

2

1

1

0

0

1. Описанная деятельность учителя направлена на формирование универсальных учебных действий учащихся

3

1

0

1. Сконструированная деятельность учащихся отражает процесс присвоения ими компонентов универсальных учебных действий

3

1

0

1. Разработанный инструментарий оценки однозначно определяет сформированность универсальных учебных действий у учащихся:

• познавательных;

• коммуникативных;

• регулятивных.

2

2

2

1

1

1

0

0

0

Всего баллов:

Количество баллов

Оценочное суждение

21 – 28 баллов

Результат сформирован

менее 21 балла

Результат не сформирован