Название: ”Алгоритмы решения задач теории чисел в Maple”
ФИО: Колесникова Анастасия Юрьевна.
Должность: Студентка
Место работы: Мордовский Государственный Педагогический Институт имени М.Е.Евсевьева
Возраст:2-3 курс
Большинство функций Maple для исcледований в области теории чисел содержатся в модуле numtheory. Для его подключения необходимо дать команду with(numtheory): .
Округление, целые и дробные части
Функция floor(x) округляет число x вниз, ceil(x) округляет число вверх, функция round(x) округляет x до ближайшего целого, функция trunc(x) возвращает floor(x) для положительных x и -floor(-x) – для отрицательных. Функция frac(x) возвращает дробную часть числа x.
Для нахождения частного при целочисленном делении используется функция iquo, для вычисления остатка от деления – функция irem. У этих функций два параметра: делимое и делитель.
Примеры:
iquo(100,3);
33
irem(100,1);
1
Также можно выполнять действия в кольце вычетов по заданному модулю. Для этого используется оператор mod у которого левый операнд – вычисляемое выражение, правый операнд – модуль, по которому проводятся вычисления. Пример нахождения обратного элемента для числа 57 в кольце вычетов по модулю 179 и проверка правильности этого вычисления:
1/57 mod 179;
22
irem(%*57,179);
1
Проверка на простоту, разложение на множители, построение простых чисел
Для проверки числа на простоту используется функция isprime, которая возвращает true, если число простое и false – если составное. Для разложения числа на множители используются функции ifactor и ifactors. Первая функция возвращает результат в виде произведения степеней простых чисел, вторая – в виде списка простых чисел и их степеней. Все эти функции работают значительно эффективней простого подбора делителей, проверка на простоту осуществляется быстрее полного разложения на множители.
Для построения простых чисел используются функции prevprime, nextprime, ithprime. Функция prevprime(n) возвращает наибольшее простое число, которое меньше n, функция nextprime(n) возвращает наименьшее простое число, которое больше n. Функция ithprime(n) возвращает n-е простое число.
Для нахождения случайного простого числа следует использовать эти функции вместе с функцией rand(), которая возвращает псевдослучайное 12-значное натуральное число. Для инициализации генератора псевдослучайных чисел необходимо использовать функцию randomize().
isprime(7!);
false
ifactor(7!);
(2)4(3)2(5)(7)
ifactors(7!);
[1, [[2, 4], [3, 2], [5, 1], [7, 1]]]
nexprime(7!);
5051
nextprime(rand());
427419669163
Специальные функции
Функция divisors(n) возвращает список всех натуральных делителей данного целого числа.
Функия tau(n) (тау-функция) возвращает количество делителей числа n.
Функия sigma(n) (сигма-функция) возвращает сумму делителей делителей числа n. Функция sigma[k](n) возвращает сумму k-х степеней делителей числа n.
Функция pi(n) (пи-функция) возвращает количество простых чисел, не превосходящих n.
Функция phi(n) (фи-функция Эйлера) возвращает количество чисел, меньших n и взаимно простых с n.
Вычисление суммы ряда и произведений.
Конечные и бесконечные суммы 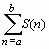 вычисляются командой прямого исполнения sum и отложенного исполнения Sum. Аргументы этих команд одинаковые: sum(expr, n=a..b), где expr – выражение, зависящее от индекса суммирования, a..b – пределы индекса суммирования, указывающие, что суммировать следует от n=a до n=b.
вычисляются командой прямого исполнения sum и отложенного исполнения Sum. Аргументы этих команд одинаковые: sum(expr, n=a..b), где expr – выражение, зависящее от индекса суммирования, a..b – пределы индекса суммирования, указывающие, что суммировать следует от n=a до n=b.
Если требуется вычислить сумму бесконечного ряда, то в качестве верхнего предела вводится infinity.
Аналогичным образом вычисляются произведения 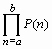 командами прямого product(P(n),n=a..b) и отложенного действийProduct P(n),n=a..b).
командами прямого product(P(n),n=a..b) и отложенного действийProduct P(n),n=a..b).
Примеры:
1. Найти полную и N-частичную суммы ряда, общий член которого равен: an=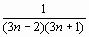 .
.
restart: a[n]:=1/((3*n-2)*(3*n+1));
an:=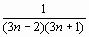
S[N]:=Sum(a[n], n=1..N)=sum(a[n], n=1..N);
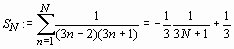
S:=limit(rhs(S[N]), N=+infinity);
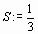
2. К какой функции сходится степенной ряд: 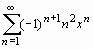 ?
?
Sum((-1)^(n+1)*n^2*x^n, n=1..infinity)=
sum((-1)^(n+1)*n^2*x^n, n=1..infinity);
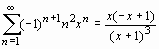 .
.
3. Найти сумму степенного ряда 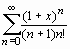 .
.
Sum((1+x)^n/((n+1)*n!), n=0..infinity)=
sum((1+x)^n/((n+1)*n!), n=0..infinity);
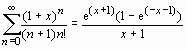
4. Найти сумму биномиального ряда 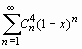 .
.
Sum(binomial(n,4)*(1-x)^n, n=1..infinity)=
sum(binomial(n,4)*(1-x)^n, n=1..infinity);
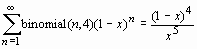
5. Вычислить бесконечное произведение: 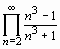
Product((n^3-1)/(n^3+1),n=2..infinity)=
product((n^3-1)/(n^3+1), n=2..infinity);
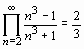 .
.
Разложение функции в степенной ряд и ряд Тейлора.
Разложение функции f(x) в степенной ряд в окрестности точки а
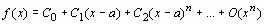
осуществляется командой series(f(x), x=a, n), где а – точка, в окрестности которой производится разложение, n – число членов ряда.
Аналогичного действия команда taylor(f(x), x=a, n) раскладывает функции f(x) в окрестности точки x=a до порядка n-1 по формуле Тейлора.
Команды series и taylor выдают результат, имеющий тип series. Для того, чтобы иметь возможность дальнейшей работы с полученным разложением, его следует преобразовать в полином с помощью команды convert(%,polynom).
Функцию многих переменных f(x1,…,xn) можно разложить в ряд Тейлора по набору переменных (x1,…,xn) в окрестности точки (a1,…,an) до порядка n с помощью команды mtaylor(f(x), [x1,…,xn], n). Эта команда находится в стандартной библиотеке, поэтому перед использованием должна быть вызвана readlib(mtaylor).
Примеры:
1. Разложить в степенной ряд 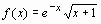 в окрестности х0=0, удерживая 5 первых членов.
в окрестности х0=0, удерживая 5 первых членов.
f(x)=series(exp(-x)*sqrt(x+1), x=0, 5);
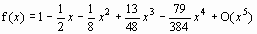
2. Разложить 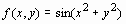 в ряд Тейлора в окрестности точки (0, 0) до 6-ого порядка.
в ряд Тейлора в окрестности точки (0, 0) до 6-ого порядка.
readlib(mtaylor):
f=mtaylor(sin(x^2+y^2), [x=0,y=0], 7);
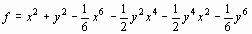
Создание собственных процедур. Разложение функции в ряд Фурье.
В Maple имеется возможность создавать собственные процедуры. Процедура начинается с заголовка. Заголовок состоит из имени процедуры (его пользователь определяет сам), далее следует обязательный оператор присваивания := и служебное слово proc, после которого в круглых скобках через запятую указываются формальные параметры процедуры.
Во избежании неполадок работы процедуры, рекомендуется в строке заголовка процедуры описывать переменные, которые будут использоваться только внутри тела процедуры (они называются локальными переменными). Для этого используется служебное слово local, после которого через запятую перечисляются локальные переменные.
После заголовка следует основное тело процедуры, состоящее из составленных пользователем команд, причем последняя команда будет выводить окончательный результат выполнения процедуры. Процедура должна обязательно оканчиваться служебным словомend.
Общий вид процедуры (стандартный синтаксис):
name:=proc(var1, var2, …) local vloc1, vloc2,…;
expr1;
expr2;
……………
exprn;
end;
В Maple нет команды, позволяющей производить разложение функции в тригонометрический ряд Фурье. Однако можно создать собственную процедуру разложения ряд Фурье. Пусть требуется разложить на интервале [x1, x2] 2l-периодическую функцию f(x). Тогда ряд Фурье имеет вид:
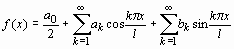 ,
,
где l=(x2- x1)/2;
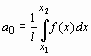 ;
; 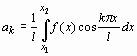 ;
; 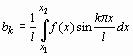 .
.
Получить первые n членов ряда Фурье можно с помощью следующей процедуры:
fourierseries:=proc(f,x,x1,x2,n) local k, l,
a, b, s;
l:=(x2-x1)/2;
a[0]:=int(f,x=x1..x2)/l;
a[k]:=int(f*cos(k*Pi*x/l),x=x1..x2)/l;
b[k]:=int(f*sin(k*Pi*x/l),x=x1..x2)/l;
s:=a[0]/2+sum(a[k]*cos(k*Pi*x/l)+
b[k]*sin(k*Pi*x/l), k=1..n);
end;
Порядок обращения к этой процедуре такой: fourierseries(f,x,x1,x2,n), где f – имя функции, разложение которой требуется найти, где х – имя независимой переменной, где х1, x2 – интервал разложения, где n – число членов ряда.


 Получите свидетельство
Получите свидетельство Вход
Вход


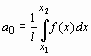 ;
; 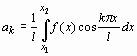 ;
; 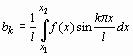 .
.








 Материал к уроку информатики "Алгоритмы решения задач теории чисел в Maple" (58 КB)
Материал к уроку информатики "Алгоритмы решения задач теории чисел в Maple" (58 КB)
 0
0 864
864 28
28 Нравится
0
Нравится
0



