Лекция по теме "Непрерывность функции. Классификация точек разрыва"

Лекция № 2

Тема. Непрерывность функции. Классификация точек разрыва

Цели:

• обобщить и расширить знания студентов о функции и свойствах числовой функции; формировать умение анализировать функцию, делать выводы о непрерывности функции и определять вид точек разрыва.

• продолжить развитие способностей к аналитическому и алгебраическому мышлению.

• продолжить воспитание у студентов познавательного интереса к математике, ответственности, чувства долга, академической самостоятельности.

Ход занятия

1. Организационный момент

1. Актуализация знаний

Непрерывность - одно из основных свойств функций. Решение о том, непрерывна данная функция или нет, позволяет судить о других свойствах исследуемой функции. Поэтому так важно исследовать функции на непрерывность.

К понятию непрерывной функции математика пришла, изучая в первую очередь различные законы движения. Пространство и время бесконечны, и зависимость, например, пути s от времени t, выраженная законом s = f(t), даёт пример непрерывной функции f(t). Непрерывно изменяется и температура нагреваемой воды, она также является непрерывной функцией от времени: T = f(t). Непрерывна и линия, если её можно начертить, не отрывая карандаш от бумаги. Эта линия и является графиком непрерывной функции.

1. Изучение нового материала

Определение: функция непрерывна в точке  , если предел функции в данной точке равен значению функции в этой точке:  .

Определение детализируется в следующих условиях:

1) Функция должна быть определена в точке  , то есть должно существовать значение  .

2) Должен существовать общий предел функции  . Это подразумевает существование и равенство односторонних пределов:  .

3) Предел функции в данной точке должен быть равен значению функции в этой точке:  .

Если нарушено хотя бы одно из трёх условий, то функция теряет свойство непрерывности в точке  .

Непрерывность функции на интервале формулируется остроумно и очень просто: функция непрерывна на интервале  , если она непрерывна в каждой точке данного интервала.

В частности, многие функции непрерывны на бесконечном интервале  , то есть на множестве действительных чисел  . Это линейная функция, многочлены, экспонента, синус, косинус и др. И вообще, любая элементарная функция непрерывна на своей области определения, так, например, логарифмическая функция   непрерывна на интервале  .

Классификация точек разрыва

Примечание: точка разрыва – это всегда отдельно взятая точка – не бывает «несколько точек разрыва подряд», то есть, нет такого понятия, как «интервал разрывов».

Данные точки в свою очередь подразделяются на две большие группы: разрывы первого рода и разрывы второго рода. У каждого типа разрыва есть свои характерные особенности, которые мы рассмотрим прямо сейчас:

Точка разрыва первого рода

Если в точке   нарушено условие непрерывности и односторонние пределы конечны, то она называется точкой разрыва первого рода.

Изобразим на чертеже график функции  :

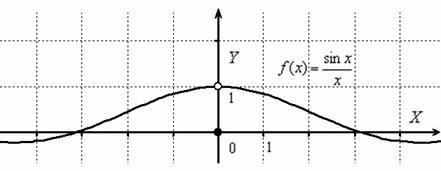
Данная функция непрерывна на всей числовой прямой, кроме точки  . И в самом деле, знаменатель же не может быть равен нулю. Однако в соответствии со смыслом предела – мы можем бесконечно близко приближаться к «нулю» и слева и справа, то есть, односторонние пределы существуют и, очевидно, совпадают:
 (Условие №2 непрерывности выполнено).

Но функция не определена в точке  , следовательно, нарушено Условие №1 непрерывности, и функция   терпит разрыв в данной точке.

Разрыв такого вида (с существующим общим пределом) называют устранимым разрывом. Почему устранимым? Потому что функцию можно доопределить в точке разрыва:

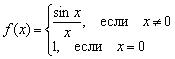
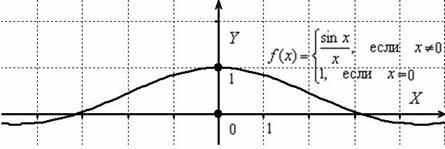
Выполним формальную проверку:
1)   – функция определена в данной точке;
2)   – общий предел существует;
3)   – предел функции в точке равен значению данной функции в данной точке.

Таким образом, все три условия выполнены, и функция непрерывна в точке   по определению непрерывности функции в точке.

В прочем, можно доопределить функцию нехорошим способом, например  :

Любопытно, что здесь выполнены первые два условия непрерывности:
1)   – функция определена в данной точке;
2)   – общий предел существует.

Но третий рубеж не пройден:  , то есть предел функции в точке не равен значению данной функции в данной точке.

Таким образом, в точке   функция терпит разрыв.

Второй случай носит название разрыва первого рода со скачком.

Рассмотрим кусочную функцию

и выполним её чертёж. Как построить график?

Очень просто. На полуинтервале   чертим фрагмент параболы   (зеленый цвет), на интервале   – отрезок прямой   (красный цвет) и на полуинтервале   – прямую   (синий цвет).

При этом в силу неравенства   значение   определено для  квадратичной функции   (зелёная точка), и в силу неравенства  , значение   определено для линейной функции   (синяя точка):

Сейчас нас будет интересовать только точка  . Исследуем её на непрерывность:

1)   – функция определена в данной точке.

2) Вычислим односторонние пределы.

Слева у нас красный отрезок прямой, поэтому левосторонний предел: 

Справа – синяя прямая, и правосторонний предел: 

В результате получены конечные числа, причем они не равны. Поскольку односторонние пределы конечны и различны:  , то наша функция терпит разрыв первого рода со скачком.

Логично, что разрыв не устраним – функцию действительно не доопределить и «не склеить», как в предыдущем примере.

Точки разрыва второго рода

Обычно к данной категории относят все остальные случаи разрыва. Чаще всего имеет место бесконечный разрыв – когда левосторонний или правосторонний, а чаще, оба предела бесконечны.

И , конечно же, самая напрашивающаяся картинка – гипербола в точке ноль. Здесь оба односторонних предела бесконечны:  , следовательно, функция   терпит разрыв второго рода в точке  .

Исследуем на непрерывность точку   по стандартной схеме:

1) Функция не определена в данной точке, поскольку знаменатель обращается в ноль.

Конечно, можно сразу сделать вывод о том, что функция терпит разрыв в точке  , но хорошо бы классифицировать характер разрыва, что часто требуется по условию. Для этого:

2) Вычислим односторонние пределы:

Напоминаю, что под записью   понимается бесконечно малое отрицательное число, а под записью   – бесконечно малое положительное число.

Односторонние пределы бесконечны, значит, функция   терпит разрыв 2-го рода в точке  . Ось ординат является вертикальной асимптотой для графика.

Н е редка ситуация, когда оба односторонних предела существуют, но бесконечен только один из них, например:
Это график функции  .

Исследуем на непрерывность точку  :

1) Функция не определена в данной точке.

2) Вычислим односторонние пределы:

Левосторонний предел конечен и равен нулю (в саму точку мы «не заходим»), но правосторонний предел бесконечен и оранжевая ветка графика бесконечно близко приближается к своей вертикальной асимптоте, заданной уравнением   (чёрный пунктир).

Таким образом, функция   терпит разрыв второго рода в точке  .

Как и для разрыва 1-го рода, в самой точке разрыва функция может быть определена. Например, для кусочной функции

смело ставим чёрную жирную точку в начале координат. Справа же – ветка гиперболы, и правосторонний предел бесконечен.

Как исследовать функцию на непрерывность?

Исследование функции на непрерывность в точке проводится по схеме, которая состоит в проверке трёх условий непрерывности:

Пример 1 Исследовать функцию   на непрерывность. Определить характер разрывов функции, если они существуют. Выполнить чертёж.

Решение:

1) Под прицел попадает единственная точка  , в которой функция не определена.

2) Вычислим односторонние пределы:

Односторонние пределы конечны и равны.

Таким образом, в точке   функция терпит устранимый разрыв.

Как выглядит график данной функции?

Хочется провести упрощение  , и вроде бы получается обычная парабола. НО исходная функция не определена в точке  , поэтому обязательна следующая оговорка:

Выполним чертёж:
Ответ: функция непрерывна на всей числовой прямой кроме точки  , в которой она терпит устранимый разрыв.

4. Подведение итогов занятия

• функция непрерывна в точке k, если предел функции в данной точке равен значению функции в этой точке: 

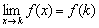
• Если в точке k нарушено условие непрерывности и односторонние пределы конечны, то она называется точкой разрыва первого рода,

• когда левосторонний или правосторонний, а чаще, оба предела бесконечны, то имеет место разрыв второго рода.

Всегда во время анализа на непрерывность необходимо помнить, что большинство известных нам функций непрерывны. К ним относятся линейная, квадратичная, показательная и тригонометрические функции.

5. Домашнее задание выучить теоретический материал, изложенный в конспекте