ПредметГеометрия
Класс10
Тема урока: КООРДИНАТЫ ВЕКТОРА В ПРОСТРАНСТВЕ. ДЕЙСТВИЯ НАД ВЕКТОРАМИ В КООРДИНАТАХ
Цели урока:Изучить, что такое “вектор в пространстве", как определяются координаты, вектора, если известны координаты его начала и конца, научитесь решать задачи, связанные с вектором.
Обобщить свои знания о векторах в координатах, узнаете о сложении векторов, вычитании векторов, умножении вектора на число, а также научитесь выполнять эти действия.
Тип урока: Изучения нового материала.
ХОД УРОКА
1. Организационный момент.
Приветствие учащихся, проверка готовности класса к уроку, организация внимания учащихся, раскрытие общих целей урока и плана его проведения.
2. Этап актуализации.
3. Формирование новых понятий и способов действия.
КООРДИНАТЫ ВЕКТОРА В ПРОСТРАНСТВЕ
В пространстве, как и на плоскости, вектором называется величина, которая задается своей длиной и направлением. Вектор изображатеся направленным отрезком, длина которого равна длине вектора. Буквально так же, как и на плоскости, определяются основные понятия для векторов в пространстве: абсолютная величина вектора, направление вектора, равенство векторов.
Но это не простое повторение, а обобщение, распространение свойств двумерной геометрии на трехмерную. Если в планиметрии для задания вектора достаточно указать две его координаты, то в стереометрии — три координаты.
Определение.Координатами вектора 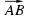 , начало которого точка A(x1,y1,z1), а конец — точка В(х2, у2, z2), называются числа a1=х2-x1, a2=y2-y1, a3=z2-z1.
, начало которого точка A(x1,y1,z1), а конец — точка В(х2, у2, z2), называются числа a1=х2-x1, a2=y2-y1, a3=z2-z1.
Записывают такой вектор, указывая его координаты: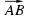 (a1 а2, а3) или
(a1 а2, а3) или 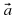 (a1 а2, а3).
(a1 а2, а3).
Например, если точкиА(4; 0; 3) и B(0; 6; 4) — начало и конец направленного отрезка 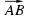 , тогда
, тогда
а1 = 0 - 4 = -4, а2 = 6- 0 = 6, а3= 4 - 3 = 1.
Значит, направленному отрезку 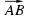 соответствует вектор
соответствует вектор 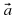 (-4; 6; 1) (рис. 67).
(-4; 6; 1) (рис. 67).
Так же, как и на плоскости, равные векторы имеют соответственно равные координаты и, обратно, векторы с соответственно равными координатами равны. Это дает основание говорить о том, что любой вектор можно отложить от любой точки пространства.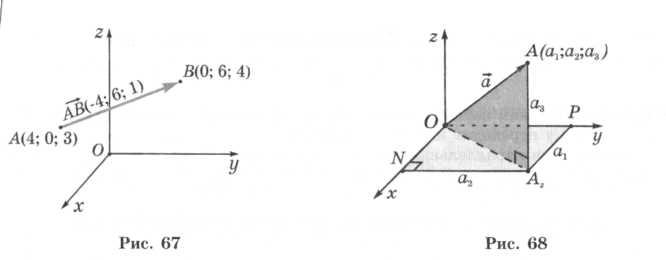
Длину вектора 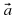 (a1 а2, а3) можно выразить через его координаты. Отложим вектор
(a1 а2, а3) можно выразить через его координаты. Отложим вектор 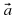 от начала координат (рис. 68). Тогда четырехугольник OPAN — прямоугольник. Его стороны равны а1и а2, поэтому ОАz2 = а12 + а22. В прямоугольном треугольнике ОА2А второй катет Аz А = а3 иОА2 = ОА2г + а32 = а12 + а22+а32. Отсюда |
от начала координат (рис. 68). Тогда четырехугольник OPAN — прямоугольник. Его стороны равны а1и а2, поэтому ОАz2 = а12 + а22. В прямоугольном треугольнике ОА2А второй катет Аz А = а3 иОА2 = ОА2г + а32 = а12 + а22+а32. Отсюда |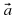 | =
| = 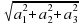
Длина любого ненулевого вектора — число положительное. Длина нулевого вектора равна нулю.
Вспомним, что два вектора, лежащих на одной прямой или параллельных прямых, называют коллинеарными. Коллинеарные векторы бывают сонаправлены(а b) или противоположно направлены (а
b) или противоположно направлены (а b). Если векторы ON и ОМколлинеарны, то точки О, N, М лежат на одной прямой. Нулевые векторы не имеют направлений и считаются коллинеарными к любому вектору.
b). Если векторы ON и ОМколлинеарны, то точки О, N, М лежат на одной прямой. Нулевые векторы не имеют направлений и считаются коллинеарными к любому вектору.
ДЕЙСТВИЯ НАД ВЕКТОРАМИ В КООРДИНАТАХ
Действия над векторами в пространстве осуществляются аналогично тому, как они определялись для векторов на плоскости.
Определение.Суммой векторов a (a1 а2, а3) и b(b1b2, b3) называется вектор а + b с координатами (а1 + b1; а2 + b2; а3 + b3)
Для любых векторов а , b и с справедливы равенства:
а+b=b+а — переместительный закон сложения;
а + (b + с) = (а+b) + с — сочетательный закон сложения.
Чтобы доказать эти свойства, достаточно сравнить соответствующие
координаты левой и правой частей каждого векторного равенства.
Для любых трех точек А, В, С в пространстве имеет место векторное равенство 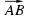 +
+ 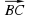 =
= 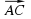 .
.
Действительно, для любых трех точек A(a1 а2, а3), B(b1b2, b3), C(c1, с2, с3) 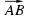 (b1– а1; b2 - а2; b3 - а3) и
(b1– а1; b2 - а2; b3 - а3) и 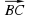 (с1 - bг; с2 - b2, с3 - b3).
(с1 - bг; с2 - b2, с3 - b3).
Отсюда 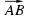 +
+ 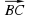 =
= 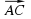 (с1– а1; с2 - а2; с3 - а3).
(с1– а1; с2 - а2; с3 - а3).
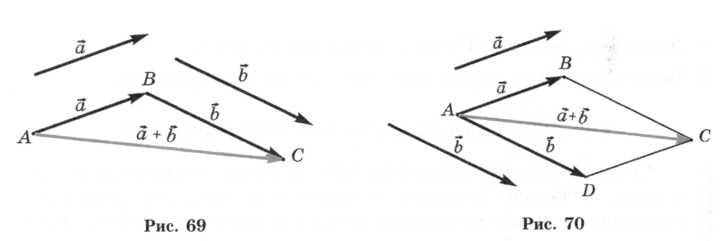
Геометрически сумму двух векторов пространства можно находить, пользуясь правилам треугольника (рис. 69).
Также применяется и правило параллелограмма. Оно часто используется в физике.
Если ABCD — параллелограмм (рис. 70), то 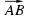 +
+ 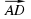 =
= 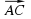 .
.
Чтобы найти сумму нескольких векторов, используем правило многоугольника. Например, если в пространстве даны точкиА, В, С, D, Е, F, то всегда
АВ + ВС +CD + DE + EF = AF.
Определение.Два вектора, сумма которых равна нулевому вектору, называются противоположными.
Из определения следует, что у противоположных векторов соответствующие координаты имеют противоположные знаки.
Определение.Разностью векторов а и b называется такой вектор с , который в сумме с вектором b дает вектор а .
Если а (а1; а2; а3) и b(b1; b2; b3), то -
=
(а1–b1;а2 - b2; а3–b3).
Определение.Произведением вектора 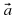 (a1; а2; a3) на число k называется вектор
(a1; а2; a3) на число k называется вектор
k = (kа1; k а2; kа3).
Из определения вытекают следующие свойства:
k(
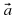 +
+ ) =k
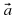 + k
+ k,
(т + n) •
=т
+п
и равенство | k •
| = | k |•|
| (здесь k, т, п — числа).
Ненулевые векторы а и bколлинеарные тогда и только тогда, когданайдется такое число х, что выполняется равенство = х
. При этом число х единственно.
4. Применение. Формирование умений и навыков.стр50. № 113-118
5.Этап информации о домашнем задании.п.п.20 стр48. №119, 120
6.Подведение итогов урока.

 Получите свидетельство
Получите свидетельство Вход
Вход












 Координаты вектора в пространстве. действия над векторами в координатах (47.18 KB)
Координаты вектора в пространстве. действия над векторами в координатах (47.18 KB)
 0
0 2796
2796 133
133 Нравится
0
Нравится
0


