Коодинатный и векторный метод в планиметрии

Координатный и векторный

методы в планиметрии

Основные формулы

-нулевой вектор

В

-противоположные векторы

С

-правило треугольника

А

С

В

- правило параллелограмма

D

А

В

-правило вычитания

С

А

- признак коллинеарности векторов

и

- скалярное произведение векторов

и

- квадрат вектора равен квадрату его длины

- абсолютная величина( длина) вектора

Основные формулы

Пусть на плоскости даны точки две прямые

, имеющие угловые коэффициенты и

- расстояние между точками А и В

-уравнение окружности с центром в точке М( а;b ) и радиусом R

- угловой коэффициент прямой АВ

- уравнение прямой проходящей через точки А и В

- условие параллельности двух прямых

- условие перпендикулярности двух прямых

- тангенс угла между двумя прямыми

- координаты точки, делящей отрезок АВ в отношении λ˃0

- координаты середины отрезка АВ

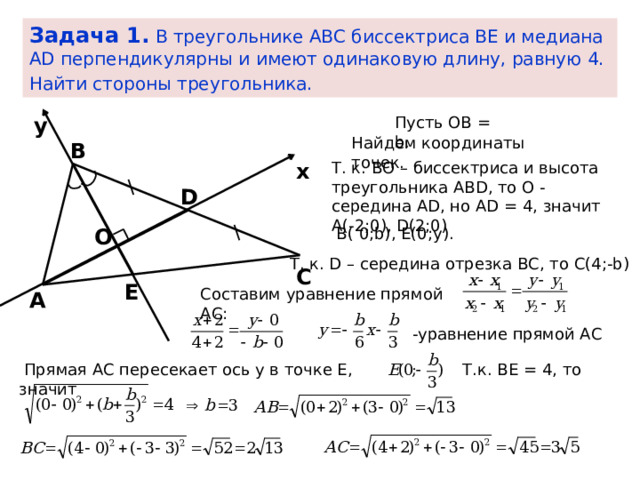
Задача 1. В треугольнике АВС биссектриса ВЕ и медиана АD перпендикулярны и имеют одинаковую длину, равную 4. Найти стороны треугольника.

Пусть ОВ = b.

y

Найдем координаты точек.

В

Т. к. ВО – биссектриса и высота треугольника ABD, то О - середина AD, но AD = 4, значит А(-2;0), D(2;0)

x

D

В( 0;b), Е(0;у).

O

Т. к. D – середина отрезка ВС, то С(4;-b)

С

Е

Составим уравнение прямой АС:

А

-уравнение прямой АС

Прямая АС пересекает ось у в точке Е, значит

Т.к. ВЕ = 4, то

Задача 2. Внутри правильного треугольника имеется

точка, удаленная от его вершин на 5, 6 и 7. Найдите площадь этого треугольника.

y

В

Пусть АМ=6, ВМ= 5, СМ=7

5

М

6

7

x

А

С

Задача 3. На сторонах AB и AD квадрата ABCD взяты

точки К и M так, что 3AK = 4AM = AB. Докажите, что прямая KM касается окружности, вписанной в квадрат.

y

Пусть АВ = 12, тогда

К

АК= 4, АМ=3, РО= R= 6

В

А

Х

М

М( 0;3 ), К( 4;6 ), О( 6;0 )

Составим уравнение прямой, проходящей через две точки М и К:

x

Р

О

-уравнение прямой МК

D

C

Составим уравнение окружности с центром О(6;0) и R=6

Убедимся, что окружность и прямая имеют единственную общую точку

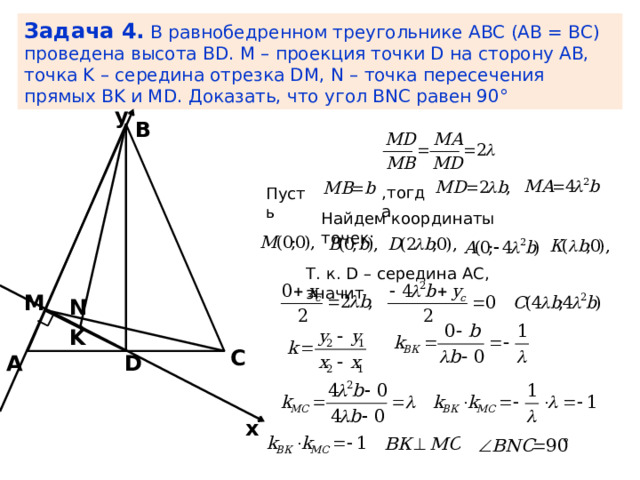
Задача 4. В равнобедренном треугольнике ABC (AB = BC) проведена высота BD. М – проекция точки D на сторону AB, точка K – середина отрезка DM, N – точка пересечения прямых BK и MD. Доказать, что угол BNС равен 90°

y

В

,тогда

Пусть

Найдем координаты точек:

Т. к. D – середина АС, значит

M

N

K

С

D

А

x

Задача 5. Расстояние между параллельными прямыми равно 6. На одной из них лежит вершина С, на другой – основание АВ равнобедренного треугольника АВС. Известно, что AB = 16 . Найти расстояние между центрами окружностей, одна из которых вписана в треугольник АВС, а вторая касается данных параллельных прямых и боковой стороны треугольника АВС

y

С

6

АС=10 по теореме Пифагора

О 2

О 3

О 1

x

А

В

Найдем координаты точек:

8

-8

О

С(0;6), В(8;0), О 1 (0;8/3), О 2 (а;3)

- уравнение окружности с центром О 2 (а;3) и R=3

или

Уравнение прямой ВС:

Задача 6 . В треугольнике ABC точка N лежит на стороне AB и AN = 3NB. Медиана AM пересекается с СN в точке O. Найти AB, если AM = CN = 7 и ∠ NOM= 60°.

В

N

M

O

А

C