Конус жана анын түрлөрү боюнча маалымат

КОНУС

Конокбаева К.М.

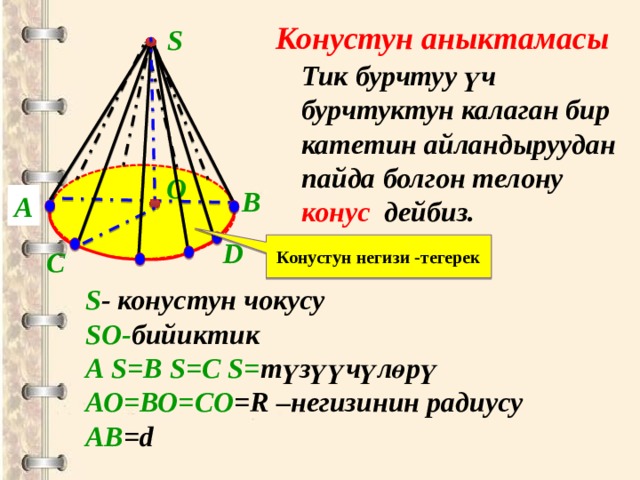
Конустун аныктамасы

S

Тик бурчтуу үч бурчтуктун калаган бир катетин айландыруудан пайда болгон телону конус дейбиз.

О

В

А

D

Конустун негизи -тегерек

С

S - конустун чокусу

SО- бийиктик

А S=В S=С S= түзүүчүлөрү

АО=ВО=СО =R –негизинин радиусу

АВ =d

Турмушта кездешүүчү конус формасындагы нерселер

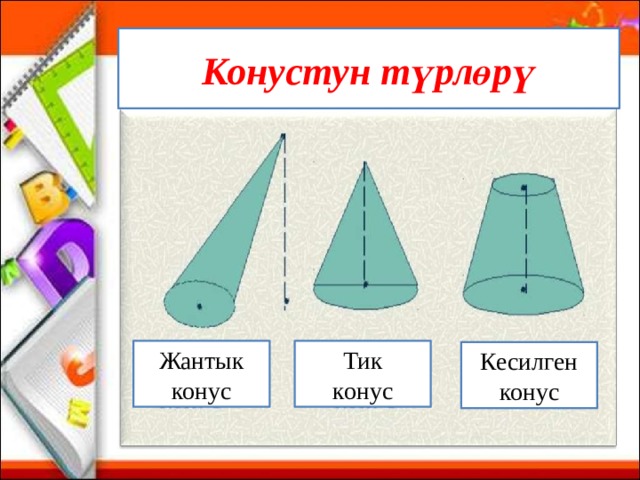
Конустун түрлөрү

Жантык конус

Тик

конус

Кесилген конус

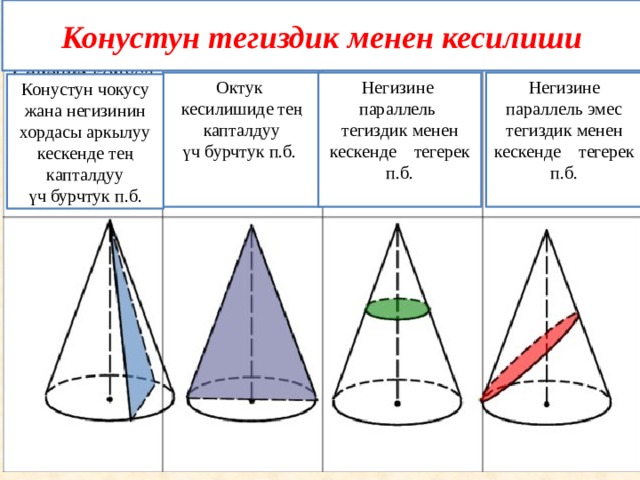
Конустун тегиздик менен кесилиши

Октук

Негизине параллель эмес тегиздик менен кескенде тегерек п.б.

Негизине параллель тегиздик менен кескенде тегерек п.б.

кесилишиде тең капталдуу

үч бурчтук п.б.

Конустун чокусу жана негизинин хордасы аркылуу кескенде тең капталдуу

үч бурчтук п.б.

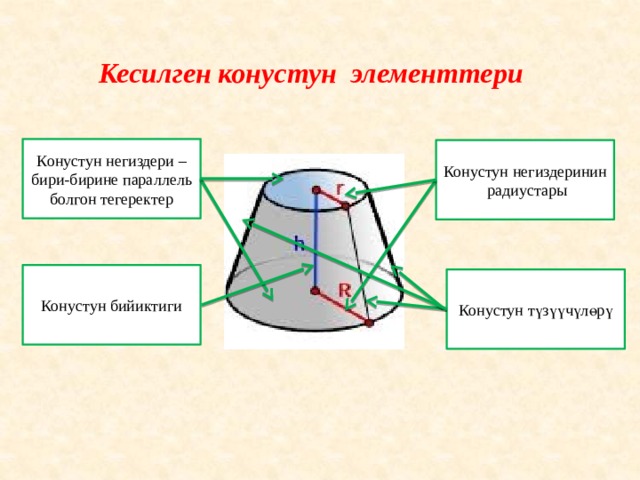
Кесилген конустун элементтери

Конустун негиздери – бири-бирине параллель болгон тегеректер

Конустун негиздеринин радиустары

Конустун бийиктиги

Конустун түзүүчүлөрү

Бетинин аянты

• S т.б = πR(R + L)
• S к.б. = πRL
• S н. = πR 2

Кесилген конус

• S т.б. = π(R + r) L + π (R 2 + r 2 )
• S т.б. = π(R + r)L

Маселе

Конустун радиусу 0,6 дм., бийиктиги 0,8 дм. Конустун түзүүчүсүн жана октук кесилишинин аянтын тапкыла.

Берилди:

АО=R= 0,6 дм.

S

SО =h= 0,8 дм.

=?дм².

АS=е =?дм.

е

Чыгаруу:

SО =h

АSО

АО =R

АS² = (0,8)²+(0,6)²

АS² = SО²+АО²

=1(дм²)

В

А

АS= 1дм.

О

АВ = d = 2 R

= 2 · 0,6

= 1 ,2 дм.

= 0,5· R · h

= 0,5·1,2 · 0,8 дм.

= 0,5·1,2 · 0,8 дм².

= 0,48дм².

АS=е =1дм.

=48 дм².

Жообу:

Үй тапшырма:

Бекбоев И.Б., Бөрүбаев А.А.

Айылчиев А.А.

Геометрия 10-11- класс

§ 29,30,31.

90- бет №4, №5.

92-бет №1, №2