Министерство общего и профессионального образования Ростовской области государственное бюджетное профессиональное образовательное учреждение
Ростовской области
«Белокалитвинский гуманитарно-индустриальный техникум»
КОНТРОЛЬНО-ИЗМЕРИТЕЛЬНЫЕ МАТЕРИАЛЫ
ДЛЯ проведения текущего КОНТРОЛЯ
ПО УЧЕБНОЙ ДИСЦИПЛИНЕ
ОУД.10 Математика: алгебра и начала математического анализа; геометрия
(индекс и наименование)
для студентов I курса
специальностей
23.02.03 Техническое обслуживание и ремонт автомобильного транспорта, укрупненная группа специальностей
08.02.09 Монтаж, наладка и эксплуатация электрооборудования промышленных и гражданских зданий
09.02.05 Прикладная информатика (по отраслям)
46.02.01 Документационное обеспечение управления и архивоведение;
40.02.01 Право и организация социального обеспечения
(код, шифр) (наименование)
Белая Калитва
2015
| РАССМОТРЕНО цикловой комиссией математических и общих естественнонаучных дисциплин |
|
| Протокол №___ от «____»______20___ |
| Председатель ЦК |
| ______________/Конькова Е.Б./ |
| Составители: | Шматко Г.В., преподаватель ГБПОУ РО «БГИТ» |
|
| Смиренская О.В., преподаватель ГБПОУ РО «БГИТ» |
ПАСПОРТ КОНТРОЛЬНЫХ ИЗМЕРИТЕЛЬНЫХ МАТЕРИАЛОВ (КИМ)
1. Область применения комплекта КИМ:
КИМ предназначен для текущего контроля и оценки результатов освоения отдельных разделов и тем общеобразовательной учебной дисциплины «Математика: алгебра и начала математического анализа; геометрия» по специальностям технического и социально-экономического профилей студентами I курса.
2. Форма контроля: контрольная работа
3. Метод контроля: письменный контроль
4. Структура работы:
Текущий контроль освоения общеобразовательной учебной дисциплины «Математика: алгебра и начала математического анализа; геометрия» осуществляется посредством выполнения студентами письменных контрольных работ. Рабочей программой их предусмотрено 11.
«Степени и корни»;
«Основы тригонометрии»;
«Степенная функция»;
«Показательная функция»;
«Логарифмическая функция»;
«Тригонометрические функции»;
«Производная и ее геометрический смысл»;
«Применение производной»;
«Тригонометрические уравнения»;
«Прямы и плоскости в пространстве»;
«Площади поверхностей и объемы геометрических тел»;
По блоку «Алгебра и начала математического анализа» общеобразовательной учебной дисциплины «Математика: алгебра и начала математического анализа; геометрия» письменные контрольные работы проводятся в традиционной форме. Каждая контрольная работа состоит из четырех вариантов заданий. В каждом варианте содержится пять заданий различной степени сложности (три первых задания обязательного уровня и еще 2 дополнительного уровня).
По блоку «Геометрия» письменные контрольные работы проводятся в форме тестирования. Каждая контрольная работа состоит из четырех вариантов. Каждый вариант состоит из заданий, которые поделены на три уровня сложности: уровень А, уровень В и уровень С.
| Наименование работы | Число заданий
| Максимальный первичный балл | Тип заданий |
| «Алгебра и начала математического анализа» |
| 1. «Степени и корни»; | 5 | - | Задания с развернутым ответом. |
| 2.«Основы тригонометрии» | 5 | - | Задания с развернутым ответом. |
| 3. «Степенная функция» | 5 | - | Задания с развернутым ответом. |
| 4. «Показательная функция»; | 5 | - | Задания с развернутым ответом. |
| 5. «Логарифмическая функция» | 5 | - | Задания с развернутым ответом. |
| 6. «Тригонометрические функции» | 5 | - | Задания с развернутым ответом. |
| 7. «Производная и ее геометрический смысл» | 5 | - | Задания с развернутым ответом. |
| 8. «Применение производной» | 5 | - | Задания с развернутым ответом. |
| 9. «Тригонометрические уравнения» | 5 | - | Задания с развернутым ответом. |
| «Геометрия» |
| 1. «Прямы и плоскости в пространстве» | 24 | 32 |
|
| Уровень А | 19 | 1 | Задания с кратким ответом |
| Уровень В | 2 | 2 | Задания с развернутым ответом. |
| Уровень С | 3 | 3 | Задания с развернутым ответом. |
| 2. «Площади поверхностей и объемы геометрических тел» | 15 | 31 |
|
| Уровень А | 5 | 1 | Задания с кратким ответом |
| Уровень В | 4 | 2 | Задания с развернутым ответом. |
| Уровень С | 6 | 3 | Задания с развернутым ответом. |
5. Распределение заданий по объектам контроля и оценки:
| Наименование объектов контроля и оценки (освоенные основные виды деятельности студентов) | Показатели оценки результата | №№ заданий для проверки |
| Раздел 2. Корни, степени, логарифмы Контрольная работа «Степени и корни» |
Преобразование числовых и буквенных выражений содержащих степени, применяя свойства; Преобразование числовых и буквенных выражений содержащих радикалы; Перевод корня n-й степени в степень с дробным показателем и наоборот; Нахождение значения степени; Выполнение преобразований выражений, применяя формулы, связанные со свойствами степеней; Решение показательных уравнений. | Производит вычисление алгебраических выражений, содержащих степени и радикалы; Демонстрирует умение преобразовывать буквенные алгебраические выражения, используя свойства степеней и свойства действий с корнями. Демонстрирует решение простейших показательных уравнений. Сравнивает числа, содержащие степени. | № 1
№ 2,4
№ 3
№ 5
|
| Раздел 3. Прямые и плоскости в пространстве Контрольная работа «Прямые и плоскости в пространстве» |
| Формулирование определений, признаков и свойств параллельных и перпендикулярных плоскостей, двугранных и линейных углов; Построение углов между прямыми, прямой и плоскостью, плоскостями по описанию, распознавание их на моделях; Применение признаков и свойств расположения прямых и плоскостей при решении задач; Изображение на рисунках перпендикуляров и наклонных к плоскости, прямых, параллельных плоскостей, углов между прямой и плоскостью, обоснование построений; Решение задач на вычисление геометрических величин; Определение и вычисление расстояний в пространстве; Применение формул и теорем планиметрии для решения задач; | Демонстрирует знание основных аксиом, определений, теорем темы «Прямые и плоскости в пространстве» Строит углы между прямыми, прямой и плоскостью, между плоскостями. Изображает на рисунках перпендикуляры и наклонные к плоскости, прямые, параллельные плоскости. Демонстрирует умение решать задач на вычисление геометрических величин. Применяет формулы и теоремы планиметрии для решения задач. | № 1-24
№ 20 - 24
|
| Раздел 6 Основы тригонометрии Контрольная работа «Основы тригонометрии» |
| Измерение радианного метода измерения углов вращения и их связи с градусной мерой; Применение основных тригонометрических тождеств для вычисления значений тригонометрических функций по одной из них; Изображение углов вращения на окружности, соотношение величины угла с его расположением; Формулирование определений тригонометрических функций для углов поворота и для острых углов прямоугольного треугольника; Изучение основных формул тригонометрии: формул сложения, удвоения, преобразования суммы тригонометрических функций в произведение и наоборот, применение этих формул при вычислении значения тригонометрического выражения и упрощении его; Ознакомление со свойствами симметрии точек на единичной окружности и применение их для вывода формул приведения; Решение по формулам и по тригонометрическому кругу простейших тригонометрических уравнений. | Демонстрирует нахождение положения точки единичной окружности, соответствующей данному углу поворота точки P(1;0) и нахождение координаты полученной точки, а также демонстрирует знание определения тригонометрических функций и их значений. Выполняет вычисление значений тригонометрических функций по одной из них с использованием основного тригонометрического тождества. Демонстрирует знание и умение использовать основные свойства и формулы при упрощении тригонометрических выражений и доказательстве тождеств. Показывает решение простейших тригонометрических уравнений. | № 1
№ 2
№ 3,4
№ 5
|
| Раздел 7 Функции и графики и Раздел 12. Уравнения и неравенства Контрольная работа «Степенная функция» |
Ознакомление с определением функции, формулирование его, нахождение области определения и области значений функции; Ознакомление с понятием графика, определение принадлежности точки графику функции, определение вида графика функции по ее формуле; Построение и чтение графиков функций; Вычисление значения функции по значению аргумента; Построение графиков степенных функций; Изучение понятия обратной функции; Решение рациональных, иррациональных, показательных, тригонометрических уравнений; Решение уравнений с применением всех приемов; Решение неравенств и их систем с применением различных способов. | Используя знания об основных свойствах степенной функции, демонстрирует нахождение области определения функции. Демонстрирует построение графика степенной функции, использую ее основные свойства. Демонстрирует знание понятия и алгоритма нахождения обратной функции и ее основные свойства. Демонстрирует решение иррациональных уравнений и неравенств, используя алгоритм решения и свойства степенной функции. | № 1,2,3
№ 2
№ 3
№ 4,5 |
| Раздел 7 Функции и графики и Раздел 12. Уравнения и неравенства Контрольная работа «Показательная функция» |
Ознакомление с определением функции, формулирование его, нахождение области определения и области значений функции; Построение и чтение графиков функций; Использование свойств функций для сравнения значений степеней и логарифмов; Использование свойств и графиков функций для решения уравнений; Решение уравнений с применением всех приемов; Решение неравенств и их систем с применением различных способов. | Производит построение графиков показательной функции, демонстрирует знание основных свойств показательной функции. Сравнивает числа, содержащие степени, используя свойства возрастания и убывания показательной функции. Приводит решение показательных уравнений и неравенств, используя алгоритм решения с применением различных способов. Приводит решение показательных уравнений и неравенств, используя алгоритм решения с применением различных способов. Приводит решение показательных неравенств и систем показательных уравнений с применением свойств показательных функций и применением различных способов и приемов; | № 1
№ 2
№ 3
№ 4,5 |
| Раздел 7 Функции и графики и Раздел 12. Уравнения и неравенства Контрольная работа «Логарифмическая функция» |
Построение и чтение графиков логарифмических функций; Использование свойств функций для сравнения значений степеней и логарифмов; Определение области допустимых значений логарифмического выражения; Выполнение преобразование выражений, применяя формулы, связанные со свойствами степеней и логарифмов; Решение логарифмических уравнений по известным алгоритмам с применением всех приемов; Решение логарифмических неравенств по известным алгоритмам с применением различных способов. | Демонстрирует построение графика логарифмической функции и определение значений функции по изменяющемуся значению аргумента. Оценивает значение логарифма и приводит обоснованное сравнение значений логарифма с использованием свойств возрастания и убывания логарифмической функции. Приводит решение логарифмических уравнений и неравенств по известным алгоритмам с использованием различных приемов. | № 1
№ 2
№ 3,4 |
| Раздел 8. Многогранники и круглые тела. Контрольная работа «Площади поверхностей и объемы геометрических тел» |
| Описание и характеристики различных видов многогранников, их элементов и свойств; Вычисление линейных элементов и углов в пространственных конфигурациях; Ознакомление с видами тел вращения, формулирование их определений и свойств; Изображение тел вращения, их разверток, сечений; Приведение доказательных рассуждений при решении задач; Изображение многогранников и круглых тел, выполнение рисунка по условию задачи; Ознакомление с понятиями площади поверхности и объема; Решение задач на вычисление площадей поверхностей и объемов геометрических тел; | Изображает многогранники и их элементы. Изображает тела вращения и их элементы, сечения тел вращения. Вычисляет площади поверхностей и объемы многогранников. Вычисляет площади поверхностей и объемы тел вращения.
| № 1, 2, 3, 6, 7,11 № 4, 5, 8, 9, 10
№ 1, 2, 3, 6, 7,11 № 4, 5, 8, 9, 10 |
| Раздел 9. Начала математического анализа. Контрольная работа «Производная и ее геометрический смысл» |
| Изучение и формулирование геометрического и механического смысла производной; Изучение алгоритма вычисления производной на примере вычисления мгновенной скорости и углового коэффициента касательной; Составление уравнения касательной в общем виде; Изучение правил дифференцирования, таблицы производных элементарных функций, применение их для дифференцирования функций и составления уравнения касательной. | Демонстрирует умение находить производные функций, используя правила дифференцирования. Показывает умение находить значение производной функции в конкретной точке. Демонстрирует знание геометрического и физического смысла производной функции. Записывает уравнение касательной к графику функции. Находит ускорение точки, движущейся по заданному закону. Находит промежутки, в которых производная функции положительна, отрицательна. | № 1-5
№1,2
№3,4,5
№3
№4
№5 |
| Раздел 9. Начала математического анализа. Контрольная работа «Применение производной» |
| Исследование функции, заданной формулой, с помощью производной; Установление связи свойств функции и производной по их графикам; Применение производной для решения задач на нахождение наибольшего, наименьшего значения и на нахождение экстремума. | Находит экстремумы функции. Находит промежутки возрастания и убывания функции. Исследует с помощью производной поведение функции на промежутке и строит ее график. Находит наибольшее и наименьшее значение функции на заданном промежутке. Демонстрирует применение производной для решения задач на нахождение наименьшей площади и периметра геометрических фигур. | №1 №2
№3
№4
№5 |
| Раздел 12 Уравнения и неравенства Контрольная работа «Тригонометрические уравнения» |
| Решение по формулам и по тригонометрическому кругу простейших тригонометрических уравнений; Применение общих методов решения уравнений и неравенств (приведение к линейному, квадратному, метод разложения на множители, замены переменной) при решении тригонометрических уравнений и неравенств; Нанесение решений простейших тригонометрических уравнений и неравенств на единичную окружность;
| Представляет решение простейших тригонометрических уравнений. Демонстрирует решение простейших тригонометрических уравнений и отбор корней на указанном промежутке. Показывает решение тригонометрических уравнений, применяя общие методы и алгоритмы решения подобных уравнений. Демонстрирует знание и умение использовать основные свойства и формулы при упрощении тригонометрических выражений, показывает решение тригонометрических уравнений и неравенств с применением общих методов решения и отбором корней с помощью единичной окружности. | №1
№2
№3
№ 4,5
|
6. Система оценивания отдельных заданий и работы в целом:
«Алгебра и начала математического анализа»
«Степени и корни»;
«Основы тригонометрии»;
«Степенная функция»;
«Показательная функция»;
«Логарифмическая функция»;
«Тригонометрические функции»;
«Производная и ее геометрический смысл»;
«Применение производной»;
«Тригонометрические уравнения»;
|
Критерии оценивания
| Баллы |
| Максимальный балл - 3 |
| Получил правильный ответ и привел полное его обоснование | 3 балла |
| Получил правильный ответ, но решение имеет незначительные недочеты, или в процессе решения допущена ошибка вычислительного или логического характера | 2 балла
|
| Существенно приблизился к правильному конечному результату или в результате нашел лишь часть правильного ответа |
| Решение начато ложным путем, но в дальнейшем отдельные этапы решения выполнены правильно (выполнены тождественные преобразования, решено простейшее уравнение и т.д.) | 1 балл |
| Решение не соответствует ни одному из приведенных выше критериев | 0 баллов |
Критерии оценки контрольной работы
| Отметка | Число баллов, необходимое для получения отметки |
| « 5» (отлично) | 15 |
| « 4» (хорошо) | 12-14,9 |
| « 3» (удовлетворительно) | 9-11,9 |
| « 2 « (неудовлетворительно) | Менее 9 |
«Геометрия»
Контрольная работа «Прямые и плоскости в пространстве».
Критерии оценки контрольной работы
| Задания | Баллы | Примечание |
| 1 - 19 | 19 | Каждый правильный ответ 1 балл |
| 20-21 | 4 | Каждый правильный ответ 2 балла |
| 22-24 | 9 | Каждый правильный ответ 3 балла |
| Итого | 32 |
|
Шкала перевода баллов в отметки
| Отметка | Число баллов, необходимое для получения отметки |
| « 5» (отлично) | 26 - 32 |
| « 4» (хорошо) | 22 - 23 |
| « 3» (удовлетворительно) | 16 - 21 |
| « 2 « (неудовлетворительно) | менее 16 |
Контрольная работа «Площади поверхностей и объемы геометрических тел»
Критерии оценки контрольной работы
| Задания | Баллы | Примечание |
| 1 – 5 | 10 | Каждый правильный ответ 2 балл |
| 6 – 9 | 12 | Каждый правильный ответ 3 балла |
| 10 – 11 | 8 | Каждый правильный ответ 4 балла |
| Итого | 30 |
|
Шкала перевода баллов в отметки
| Отметка | Число баллов, необходимое для получения отметки |
| « 5» (отлично) | 20 – 30 (не менее одного задания из уровня С) |
| « 4» (хорошо) | 16 – 25 (не менее двух заданий из уровня В) |
| « 3» (удовлетворительно) | 10 – 15 |
| « 2 « (неудовлетворительно) | менее 10 |
7. Ресурсы, необходимые для проведения контроля и оценки:
Во время проведения письменных контрольных работ у каждого обучающегося должны быть следующие материалы и оборудование:
8. Норма времени:
На выполнение работы отводится 45 минут.
СОДЕРЖАНИЕ КИМ.
Контрольная работа «Корни и степени»
Вариант №1
1. Вычислите:
| 1) 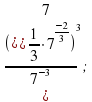 | 2) 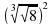
|
2. Упростите выражение
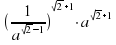
3. Решите уравнение
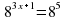
4. Сократите дробь
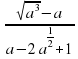
5. Сравните числа
Вариант №2
1. Вычислите:
| 1) 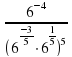 | 2) 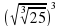
|
2. Упростите выражение
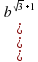
3. Решите уравнение
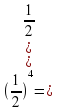
4. Сократите дробь
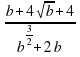
5. Сравните числа
Вариант №3
1. Вычислите:
| 1) 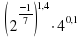 | 2) 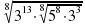
|
2. Упростите выражение
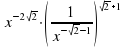
3. Решите уравнение
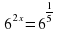
4. Сократите дробь
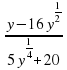
5. Сравните числа
Вариант №4
1. Вычислите:
| 1) | 2) 
|
2. Упростите выражение
3. Решите уравнение

4. Сократите дробь

5. Сравните числа
Контрольная работа «Степенная функция»
Вариант № 1
Найдите область определения функции:
а)  ; б)
; б) 
Постройте график функции  . Найдите ее область определения и множество значений.
. Найдите ее область определения и множество значений.
Найдите функцию, обратную данной, ее область определения и множество значений:  .
.
Решите уравнение:
а)  б)
б)  .
.
Решить неравенство 
Вариант № 2
Найдите область определения функции:
а)  ; б)
; б) 
Постройте график функции  . Найдите ее область определения и множество значений.
. Найдите ее область определения и множество значений.
Найдите функцию, обратную данной, ее область определения и множество значений:  .
.
Решите уравнение:
а)  б)
б)  .
.
Решить неравенство 
Вариант № 3
Найдите область определения функции:
а)  б)
б) 
Постройте график функции  . Найдите ее область определения и множество значений.
. Найдите ее область определения и множество значений.
Найдите функцию, обратную данной, ее область определения и множество значений:  .
.
Решите уравнение:
а)  б)
б) 
Решить неравенство 
Вариант № 4
Найдите область определения функции:
а)  б)
б) 
Постройте график функции  . Найдите ее область определения и множество значений.
. Найдите ее область определения и множество значений.
Найдите функцию, обратную данной, ее область определения и множество значений:  .
.
Решите уравнение:
а)  б)
б) 
Решить неравенство 
Контрольная работа «Показательная функция»
Вариант № 1
Изобразите схематически график функции  и опишите по графику ее свойства.
и опишите по графику ее свойства.
Сравните числа:
а)
Решите уравнение:
а)  б)
б) 
Решите неравенство: 
Решите систему уравнений:
Вариант № 2
Изобразите схематически график функции  и опишите по графику ее свойства.
и опишите по графику ее свойства.
Сравните числа:
а)
Решите уравнение:
а)  б)
б) 
Решите неравенство: 
Решите систему уравнений:
Вариант № 3
Изобразите схематически график функции  и опишите по графику ее свойства.
и опишите по графику ее свойства.
Сравните числа:
а)
Решите уравнение:
а) б) 
Решите неравенство:
Решите систему уравнений:
Вариант № 4
Изобразите схематически график функции и опишите по графику ее свойства.
Сравните числа:
а)
Решите уравнение:
а)  б)
б) 
Решите неравенство:
Решите систему уравнений:
Контрольная работа «Логарифмическая функция»
Вариант № 1
Построить график функции  . Как изменяется y, когда x возрастает от
. Как изменяется y, когда x возрастает от  до 8?
до 8?
Вычислить: а)  б)
б) 
в)
Сравнить числа:
Решить уравнение: а)  б)
б) 
Решить неравенство:
Вариант № 2
Построить график функции  . Как изменяется y, когда x возрастает от
. Как изменяется y, когда x возрастает от  до 16?
до 16?
Вычислить: а)  б)
б)
в)
Сравнить числа:
Решить уравнение: а) б) 
Решить неравенство:
Вариант № 3
Построить график функции  . Как изменяется y, когда x возрастает от
. Как изменяется y, когда x возрастает от  до 4?
до 4?
Вычислить: а)  б)
б)
в)
Сравнить числа:
Решить уравнение: а) б)
Решить неравенство:
Вариант № 4
Построить график функции  . Как изменяется y, когда x убывает от
. Как изменяется y, когда x убывает от  до
до  ?
?
Вычислить: а)  б)
б) 
в)
Сравнить числа: 
Решить уравнение: а)  б)
б)
Решить неравенство:
Контрольная работа «Прямые и плоскости в пространстве».
1 вариант
Уровень А.
У треугольника основание равно 18 см. Чему равна средняя линия треугольника?
Основания трапеции равны 12см и 7см. Чему равна средняя линия трапеции?
Разность двух углов параллелограмма равна 40°. Найдите его углы.
Могут ли быть перпендикулярны к одной плоскости две стороны одного треугольника?
Верно ли, что если три данные точки лежат в одной плоскости, то они не лежат на одной прямой?
Даны точкиА, В, С и D. Плоскость α проходит через прямую АВ, но не проходит через точку С. Прямые AD и BC пересекаются в точке В. Сколько данных точек лежит в плоскости α?
Верно ли, что если концы отрезка лежат в данной плоскости, то и его середина лежит в этой плоскости?
Определите взаимное расположение прямых а иb, если прямаяа лежит в плоскости α, а прямая bпересекает плоскость α в точке, не лежащей на прямой а.
Определите взаимное расположение прямой а и плоскости α , если а || b, и прямая b пересекает плоскость α?
Поставьте вместо пропуска слова «прямой» или «плоскости» так, чтобы данное утверждение было верным: «Две прямые, параллельные некоторой . . . , параллельны».
Верно ли, что плоскость, перпендикулярная к данной прямой, перпендикулярна к любой плоскости, содержащей эту прямую?
Из точкиА к плоскости  проведены перпендикуляр
проведены перпендикуляр  и наклонная
и наклонная  . В плоскости
. В плоскости  проведена прямая
проведена прямая  , перпендикулярная к
, перпендикулярная к  . Назовите плоскость, перпендикулярную к плоскости
. Назовите плоскость, перпендикулярную к плоскости  .
.
Из точки  , не лежащей в плоскости треугольника
, не лежащей в плоскости треугольника  и равноудалённой от его вершин, к плоскости
и равноудалённой от его вершин, к плоскости  проведён перпендикуляр
проведён перпендикуляр  . Определите вид треугольника
. Определите вид треугольника  , если точка О лежит на стороне
, если точка О лежит на стороне  .
.
Верно ли, что две прямые, перпендикулярные к одной плоскости, параллельны?
Может ли прямая, перпендикулярная к плоскости, быть параллельна прямой, лежащей в этой плоскости?
Даны прямые  и
и  , и плоскость
, и плоскость  . Определите угол между данными прямыми, если
. Определите угол между данными прямыми, если  ||
|| .
.
 - перпендикуляр к плоскости прямоугольника
- перпендикуляр к плоскости прямоугольника  . Назовите отрезок, изображающий расстояние от точки
. Назовите отрезок, изображающий расстояние от точки  до прямой
до прямой  .
.
Через сторону  треугольника
треугольника  проведена плоскость
проведена плоскость  .
.  - перпендикуляр к плоскости
- перпендикуляр к плоскости  . Назовите угол между прямой
. Назовите угол между прямой  и плоскостью
и плоскостью  .
.
Верно ли, что расстояние между параллельными плоскостями равно расстоянию от любой прямой одной плоскости до другой плоскости?
Уровень В.
Перекладина длиной 5 м лежит своими концами на двух вертикальных столбах высотой 3 м
и 6 м. Каково расстояние между основаниями столбов?
Из точки А к плоскости проведены перпендикуляр и наклонная, длина которой 20 см. Угол между наклонной и плоскостью равен 60°. Найдите длину перпендикуляра.
Уровень С.
Расстояние от точки М до каждой из вершин правильного треугольника ABCравно 4см. Найдите расстояние от точки Mдо плоскости ABC, если AB = 6см.
Расстояние от точкиМ до сторон квадрата равно13см. Найдите расстояние от точки М до плоскости квадрата, если сторона квадрата равна 10см.
Из точки к плоскости проведены две наклонные. Первая наклонная равна 20см и образует с плоскостью угол 30°. Длина второй наклонной  см. Какой угол образует с плоскостью вторая наклонная?
см. Какой угол образует с плоскостью вторая наклонная?
2 вариант
Уровень А.
У треугольника основание равно 10 см. Чему равна средняя линия треугольника?
Основания трапеции равны 13см и 4см. Чему равна средняя линия трапеции?
Величины двух углов параллелограмма относятся как 7:11. Найдите эти углы.
Могут ли быть перпендикулярны к одной плоскости две стороны трапеции?
Могут ли две плоскости иметь общую точку, но не иметь общей прямой?
Плоскости CBD и EDC пересекаются по прямой а. Назовите две точки, лежащие на прямой а.
Три прямые пересекаются в точке А. Через данную точку необходимо провести плоскость, содержащую ровно две из трёх данных прямых. Сколько таких плоскостей можно провести?
Дана плоскость  и прямые а, bи с. Известно, что одна из данных прямых параллельна плоскости
и прямые а, bи с. Известно, что одна из данных прямых параллельна плоскости  . Назовите эту прямую, еслиа || с, прямые bи с пересекаются, а прямая с лежит в плоскости
. Назовите эту прямую, еслиа || с, прямые bи с пересекаются, а прямая с лежит в плоскости  .
.
Поставьте вместо пропуска слова «прямая» или «плоскость» так, чтобы данное утверждение было верным: «Если некоторая . . . параллельна каждой из двух данных прямых, то данные прямые могут пересекаться».
Верно ли, что если две прямые в пространстве не пересекаются, то они параллельны?
Может ли расстояние от точки до плоскости изображаться двумя различными отрезками?
Дан прямоугольный треугольник  с гипотенузой
с гипотенузой  .
.  - перпендикуляр к плоскости треугольника. Назовите линейный угол двугранного угла между плоскостями
- перпендикуляр к плоскости треугольника. Назовите линейный угол двугранного угла между плоскостями  и
и  .
.
Верно ли, что три взаимно перпендикулярные прямые определяют в пространстве три взаимно перпендикулярные плоскости?
Верно ли, что прямая перпендикулярна к плоскости, если она перпендикулярна к двум прямым этой плоскости?
Могут ли две скрещивающиеся прямые быть перпендикулярными к одной плоскости?
Даны прямые  ,
,  и
и  , и плоскость
, и плоскость  . Укажите среди данных прямых прямую, перпендикулярную к двум другим, если
. Укажите среди данных прямых прямую, перпендикулярную к двум другим, если  ||
|| ,
,  лежит в плоскости
лежит в плоскости  .
.
Точка D – середина гипотенузы  прямоугольного треугольника
прямоугольного треугольника  .
.  - прямая, перпендикулярная к плоскости
- прямая, перпендикулярная к плоскости  . Назовите отрезки, равные отрезку
. Назовите отрезки, равные отрезку  .
.
 - перпендикуляр к плоскости треугольника
- перпендикуляр к плоскости треугольника  . Назовите наибольшую сторону треугольника, если
. Назовите наибольшую сторону треугольника, если  .
.
Могут ли две прямые, образующие с данной плоскостью неравные углы, быть параллельными?
Уровень В.
Какой длины нужно взять перекладину, чтобы её можно было положить концами на две
вертикальные опоры высотой 4 м и 8 м, поставленные на расстоянии 3 м одна от другой?
Из точки А к плоскости проведены перпендикуляр и наклонная. Длина наклонной4 см, а длина перпендикуляра  см. Найдите угол между наклонной и плоскостью.
см. Найдите угол между наклонной и плоскостью.
Уровень С.
Расстояние от точкиК до каждой из вершин квадрата ABCDравно 5см. Найдите расстояние от точки Kдо плоскости ABC, если AB =3 см.
см.
Точка М находится на одинаковом расстоянии от всех сторон правильного треугольника со стороной 12см и удалена от плоскости треугольника на 6см. Найдите расстояние от точки М до сторон треугольника.
Из точки к плоскости проведены две наклонные. Первая наклонная равна 12см и образует с плоскостью угол 30°. Проекция второй наклонной 8см. Найдите длину второй наклонной.
3 вариант
Уровень А.
У треугольника основание равно 16 см. Чему равна средняя линия треугольника?
Основания трапеции равны 15см и 6см. Чему равна средняя линия трапеции?
Углы треугольника пропорциональны числам 3:7:8. Определить наибольший угол треугольника.
Могут ли быть перпендикулярны к одной плоскости две стороны одного ромба?
ТочкаА не лежит в плоскости KMN. Назовите прямую пересечения плоскостей AMN и AKM.
Верно ли, что если через четыре точки проходит плоскость, то такая плоскость – единственная?
Даны точкиА, В, С и D. Плоскость α проходит через точкиВ, С и D, но не проходит через точку А. Назовите три из данных точек, которые могут лежать на одной прямой.
Определите взаимное расположение прямой а и плоскости α , если в плоскости α не существует прямой, пересекающей а.
Верно ли, что две прямые, параллельные одной плоскости, параллельны?
Поставьте вместо пропуска слова «прямая» или «плоскость» так, чтобы данное утверждение было верным: «Если некоторая . . . пересечена тремя данными параллельными прямыми, то данные прямые лежат в одной плоскости».
 - перпендикуляр к плоскости треугольника
- перпендикуляр к плоскости треугольника  . Назовите угол между прямой
. Назовите угол между прямой  и плоскостью
и плоскостью  .
.
Может ли расстояние между двумя параллельными рёбрами куба быть больше длины его ребра?
Может ли расстояние между плоскостями оснований параллелепипеда быть больше длины любого его ребра?
ТочкаО – центр окружности, описанной около треугольника  .
.  - прямая, перпендикулярная к плоскости
- прямая, перпендикулярная к плоскости  . Назовите отрезки, равные отрезку
. Назовите отрезки, равные отрезку  .
.
Верно ли, что любая из трёх взаимно перпендикулярных прямых перпендикулярна к плоскости двух других прямых?
Могут ли пересекаться две плоскости, перпендикулярные к одной прямой?
Даны прямые  ,
,  ,
,  ,
,  и плоскость
и плоскость  . Укажите среди данных прямых параллельные, если
. Укажите среди данных прямых параллельные, если  и
и  лежат в
лежат в  ,
,  .
.
Точка  - точка пересечения диагоналей ромба
- точка пересечения диагоналей ромба  .
.  - перпендикуляр к плоскости ромба. Назовите отрезок, изображающий расстояние от точки
- перпендикуляр к плоскости ромба. Назовите отрезок, изображающий расстояние от точки  до прямой
до прямой  .
.
Верно ли, что отрезок, изображающий расстояние междускрещивающимися прямыми, является перпендикуляром к каждой из них?
Уровень В
Перекладина длиной 10 м лежит своими концами на двух вертикальных столбах высотой 13 м и 7 м. Каково расстояние между основаниями столбов?
Из точки А к плоскости проведены перпендикуляр и наклонная, длина которой 10 см. Угол между наклонной и плоскостью равен 30°. Найдите длину перпендикуляра.
Уровень С.
Точка О – центр квадрата со стороной 4см. АО – перпендикуляр к плоскости квадрата, АО= см. Найдите расстояние от точки А до вершин квадрата.
см. Найдите расстояние от точки А до вершин квадрата.
Точка М находится на одинаковом расстоянии от всех сторон правильного треугольника и удалена от плоскости треугольника на  см. Угол между перпендикуляром и наклонной, проведенными из точки М к плоскости треугольника, равен 60°.Найдите сторону этого треугольника.
см. Угол между перпендикуляром и наклонной, проведенными из точки М к плоскости треугольника, равен 60°.Найдите сторону этого треугольника.
Из точки к плоскости проведены две наклонные. Первая наклонная равна  см и образует с плоскостью угол 45°. Длина второй наклонной 13см. Найдите проекцию второй наклонной.
см и образует с плоскостью угол 45°. Длина второй наклонной 13см. Найдите проекцию второй наклонной.
4 вариант
Уровень А.
У треугольника основание равно 22 см. Чему равна средняя линия треугольника?
Основания трапеции равны 17см и 8см. Чему равна средняя линия трапеции?
В равнобедренном треугольнике ABC с основанием AC внешний угол у вершины A равен 150o. Найти угол  ABC.
ABC.
Могут ли быть перпендикулярны к одной плоскости две стороны квадрата?
В пространстве даны прямая и точка. Сколько различных плоскостей можно через них провести?
Могут ли три прямые, пересекающиеся в одной точке, определять в пространстве ровно две плоскости?
Даны точкиА, В, С, Dи Е. Плоскость α проходит через точки А и В, но не проходит через точки С,D и Е. Среди данных точек назовите точку, которая не может лежать на прямой AD.
Верно ли, что если одна из двух параллельных прямых лежит в некоторой плоскости, то и вторая прямая лежит в этой плоскости?
Дана плоскость  и прямые а, bи с, причём две из трёх данных прямых параллельны. Назовите параллельные прямые, если прямаяа лежит в плоскости
и прямые а, bи с, причём две из трёх данных прямых параллельны. Назовите параллельные прямые, если прямаяа лежит в плоскости  , b||
, b|| , а прямая с пересекает плоскость
, а прямая с пересекает плоскость  .
.
Поставьте вместо пропуска слова «параллельны», «пересекаются» или «скрещиваются» так, чтобы данное утверждение было верно на плоскости, но неверно в пространстве: «Если две прямые не имеют общих точек, то они . . .».
Из точкиА к плоскости  проведены перпендикуляр
проведены перпендикуляр  и наклонная
и наклонная  . В плоскости
. В плоскости  через точку С проведена прямая l, перпендикулярная к
через точку С проведена прямая l, перпендикулярная к  . Назовите ещё две прямые, перпендикулярные к l.
. Назовите ещё две прямые, перпендикулярные к l.
Верно ли, что плоскости  и
и  , проходящие через перпендикулярные прямые
, проходящие через перпендикулярные прямые  и
и  соответственно, также перпендикулярны?
соответственно, также перпендикулярны?
 - перпендикуляр к плоскости прямоугольника
- перпендикуляр к плоскости прямоугольника  . Назовите линейный угол двугранного угла между плоскостями
. Назовите линейный угол двугранного угла между плоскостями  и
и  .
.
 - прямая, перпендикулярная к плоскости равностороннего треугольника
- прямая, перпендикулярная к плоскости равностороннего треугольника  . Назовите отрезок, равный отрезку
. Назовите отрезок, равный отрезку  .
.
Верно ли, что длина перпендикуляра меньше длины наклонной, проведённой из той же точки?
Может ли угол между прямой и плоскостью быть тупым?
 - перпендикуляр к плоскости треугольника
- перпендикуляр к плоскости треугольника  . Определите вид треугольника
. Определите вид треугольника  , если
, если  .
.
Может ли прямая пересекать параллельные плоскости под разными углами?
Через сторону  прямоугольника
прямоугольника  проведена плоскость
проведена плоскость  .
.  - перпендикуляр к плоскости
- перпендикуляр к плоскости  . Назовите угол между прямой
. Назовите угол между прямой  и плоскостью
и плоскостью  .
.
Уровень В.
Какой длины нужно взять перекладину, чтобы её можно было положить концами на две
вертикальные опоры высотой 12 м и 24 м, поставленные на расстоянии 9 м одна от другой?
Из точки А к плоскости проведены перпендикуляр и наклонная. Наклонная образует с плоскостью угол 45°, а длина перпендикуляра  см. Найдите длину наклонной.
см. Найдите длину наклонной.
Уровень С.
Расстояние от точкиК до каждой из вершин квадрата ABCDравно 5см. Найдите расстояние от точки Kдо плоскости квадрата, если диагональ квадрата равна 6см.
Периметр правильного треугольника равен  см, а расстояние от точки М до каждой из сторон треугольника равно 10см. Найдите расстояние от точки М до плоскости треугольника.
см, а расстояние от точки М до каждой из сторон треугольника равно 10см. Найдите расстояние от точки М до плоскости треугольника.
Из точки к плоскости проведены две наклонные. Первая наклонная равна  см и образует с плоскостью угол 30°. Угол между перпендикуляром и второй наклонной 45°. Найдите длину второй наклонной.
см и образует с плоскостью угол 30°. Угол между перпендикуляром и второй наклонной 45°. Найдите длину второй наклонной.
Контрольная работа «Основы тригонометрии»
Вариант № 1
Вычислить: а)  ; б)
; б)  .
.
Вычислить:
Упростить выражение: а) 
б)
Докажите тождество:
Решите уравнение: 
Вариант № 2
Вычислить: а)  ; б)
; б)  .
.
Вычислить:
Упростить выражение: а) 
б)
Докажите тождество:
Решите уравнение: 
Вариант № 3
Вычислить: а)  ; б)
; б)  .
.
Вычислить:
Упростить выражение: а) 
б)
Докажите тождество: 
Решите уравнение: 
Вариант № 4
Вычислить: а)  ; б)
; б)  .
.
Вычислить:
Упростить выражение: а) 
б)
Докажите тождество:
Решите уравнение: 
Контрольная работа «Тригонометрические уравнения»
Вариант № 1
Решить уравнение:
 ;
;

Найти корни уравнения  на отрезке
на отрезке 
Решить уравнение:


Найдите наибольший отрицательный корень уравнения: 
Решить неравенство: 
Вариант № 2
Решить уравнение:
 ;
;

Найти корни уравнения  на отрезке
на отрезке 
Решить уравнение:

-
Найдите наибольший отрицательный корень уравнения: 
Решить неравенство: 
Вариант № 3
Решить уравнение:
 ;
;

Найти корни уравнения  на отрезке
на отрезке 
Решить уравнение:


Найдите наибольший отрицательный корень уравнения: 
Решить неравенство: 
Вариант № 4
Решить уравнение:
 ;
;

Найти корни уравнения  на отрезке
на отрезке 
Решить уравнение:

-
Найдите наибольший отрицательный корень уравнения: 
Решить неравенство: 
Контрольная работа «Площади поверхностей и объемы геометрических тел»
1вариант
Уровень А.
Ребро куба равно 5см. Найдите площадь боковой поверхности и объем куба.
Найти объем прямой призмы, в основании которой лежит ромб с диагоналями 10см и 18см, а боковое ребро равно 5см.
Сторона основания правильной треугольной пирамиды равна 4см, а высота 6см. Найдите объем пирамиды.
Найдите площадь боковой поверхности и объем цилиндра с высотой, равной 3см и диаметром 6см.
Найдите площадь полной поверхности конуса, образующая которого равна 10см, а в осевое сечение – правильный треугольник.
Уровень В.
Основание прямой призмы - прямоугольный треугольник с катетом 5 см и гипотенузой 13 см. Высота призмы равна 10 см. Найдите объём призмы.
В правильной треугольной пирамиде апофема равна 2см и образует с высотой пирамиды угол 60°. Найдите площадь боковой поверхности пирамиды.
Высота цилиндра равна 4 см, расстояние между осью цилиндра и параллельной ей плоскостью сечения равно 3 см, а площадь сечения 32 см2. Найдите площадь боковой поверхности цилиндра.
Найдите объем конуса, если диагональ квадрата, описанного вокруг основания конуса, равна  см, а высота конуса равна 6см.
см, а высота конуса равна 6см.
Уровень С.
Площадь сечения, не проходящего через центр шара, равна 16π см2. Найдите площадь поверхности и объем шара, если расстояние от центра шара до секущей плоскости равно 5м.
Апофема правильной треугольной пирамиды равна l и образует с высотой пирамиды угол β. Найдите объем пирамиды.
2вариант
Уровень А.
Основание прямой треугольной призмы – прямоугольный треугольник с катетами 3см и 4см. Высота призмы 10см. Найдите площадь полной поверхности призмы.
В основании прямой призмы лежит равнобедренная трапеция с основаниями 4см и 10см и боковой стороной 5см. Боковое ребро призмы равно 10см. Найдите площадь полной поверхности призмы.
Основание пирамиды – прямоугольный треугольник с катетами 6см и 8см. Высота пирамиды равна 10см. Найдите объем пирамиды.
Осевое сечение цилиндра – квадрат со стороной 8см. Найдите площадь боковой поверхности и объем цилиндра.
Площадь основания конуса равна 25π см2, а его образующая 10см. Найдите площадь боковой поверхности конуса.
Уровень В.
Основание прямой призмы – треугольник со сторонами 5см, 5см и 6см. Диагональ меньшей боковой грани образует угол 45° с боковым ребром призмы. Найдите объем призмы.
Апофема правильной треугольной пирамиды равна 6см, а радиус окружности, вписанной в ее основание, равен  см. Найдите площадь боковой поверхности пирамиды.
см. Найдите площадь боковой поверхности пирамиды.
Высота цилиндра равна 10см. В нижнем основании цилиндра на расстоянии  см от центра проведена хорда, которую видно из центра этого основания под углом 60°. Найдите объем цилиндра.
см от центра проведена хорда, которую видно из центра этого основания под углом 60°. Найдите объем цилиндра.
Найдите объем конуса, если сторона правильного треугольника, вписанного в основание конуса, равна 6см, а высота конуса равна 8см.
Уровень С.
Линия пересечения сферы и плоскости, удаленной от центра на 12см, имеет длину 10π см. Найдите площадь поверхности и объем шара.
В правильной треугольной пирамиде боковое ребро равно b, а плоский угол при вершине пирамиды равен 2β. Найдите площадь полной поверхности пирамиды.
3вариант
Уровень А.
Основание прямой треугольной призмы – прямоугольный треугольник с катетами 5см и 12см. Боковое ребро призмы 8см. Найдите объем призмы.
В основании прямой призмы лежит прямоугольник со сторонами 8см и 6см. Боковое ребро призмы равно 10см. Найдите площадь полной поверхности призмы.
Основанием пирамиды является ромб с острым углом 30° и стороной 4см. Найдите объем пирамиды, если ее высота равна 15см.
Диагональ осевого сечения цилиндра равна 10см и образует с плоскостью основания угол 30°. Найдите объем цилиндра.
Образующая конуса равна 14см, угол при вершине осевого сечения равен 60°. Найдите площадь полной поверхности конуса.
Уровень В.
В основании прямой призмы лежит треугольник со сторонами 7см, 5см и 6см. Диагональ большей боковой грани образует угол 45° с ребром при основании призмы. Найдите объем призмы.
Апофема правильной треугольной пирамиды равна 6см, а плоский угол при вершине 90°. Найдите площадь боковой поверхности пирамиды.
Радиус цилиндра равен 10см. Параллельно оси цилиндра на расстоянии 8см от нее проведено сечение, диагональ которого равна 13см. Найдите объем цилиндра.
Найдите объем конуса, если сторона правильного треугольника, описанного вокруг основания конуса, равна  см, а высота конуса равна 10см.
см, а высота конуса равна 10см.
Уровень С.
Сечение сферы плоскостью, удаленной от ее центра на 15см, имеет площадь 64π см2. Найдите площадь поверхности и объем шара.
В правильной треугольной пирамиде боковое ребро равно b и образует с высотой пирамиды угол α. Найдите объем пирамиды.
4вариант
Уровень А.
В основании призмы лежит ромб со стороной 5см и острым углом 30°. Высота призмы 6см. Найдите объем призмы.
В основании прямой призмы лежит прямоугольник со стороной 6см и диагональю 10см. Боковое ребро призмы равно 10см. Найдите площадь боковой поверхности призмы.
Основанием пирамиды является ромб с диагоналями 6см и 9см. Найдите объем пирамиды, если ее высота равна 11см.
Диагональ осевого сечения цилиндра равна 12см и образует с основанием угол 60°. Найдите площадь боковой поверхности цилиндра.
Найдите площадь полной поверхности конуса, образующая которого равна 8см и наклонена к основанию под углом 60°.
Уровень В.
В правильной треугольной призме диагональ боковой грани образует со стороной основания угол 30° и равна 4см. Найдите объем призмы.
Радиус окружности, описанной около основания правильной четырехугольной пирамиды, равен  см, а апофема – 10см. Найдите площадь боковой поверхности пирамиды.
см, а апофема – 10см. Найдите площадь боковой поверхности пирамиды.
Высота цилиндра равна 6см. В нижнем основании цилиндра на расстоянии  см от центра проведена хорда, которую видно из центра этого основания под углом 90°. Найдите объем цилиндра.
см от центра проведена хорда, которую видно из центра этого основания под углом 90°. Найдите объем цилиндра.
Найдите объем конуса, если сторона квадрата, вписанного в основание конуса равна 4см, а высота конуса равна 5см.
Уровень С.
Линия пересечения сферы и плоскости, удаленной от центра на 12см, имеет длину 32π см. Найдите площадь поверхности и объем шара.
В правильной треугольной пирамиде боковое ребро равно b, а плоский угол при основании пирамиды равен β. Найдите площадь полной поверхности пирамиды.
Контрольная работа «Производная и ее геометрический смысл»
Вариант № 1
Найти производную функции:
 ;
;
 ;
;
 ;
;

Найти значение производной функции  в точке
в точке  , если .
, если .
Записать уравнение касательной к графику функции в точке  .
.
Точка движется прямолинейно по закону  . Найдите ее ускорение в момент времени
. Найдите ее ускорение в момент времени  (координата
(координата  измеряется в сантиметрах, время t – в секундах).
измеряется в сантиметрах, время t – в секундах).
Найти значения  , при которых значения производной функции
, при которых значения производной функции  положительны.
положительны.
Вариант № 2
Найти производную функции:
 ;
;
 ;
;
 ;
;

Найти значение производной функции  в точке
в точке  , если .
, если .
Записать уравнение касательной к графику функции  в точке
в точке  .
.
Точка движется прямолинейно по закону  . Найдите ее ускорение в момент времени
. Найдите ее ускорение в момент времени  (координата
(координата  измеряется в сантиметрах, время t – в секундах).
измеряется в сантиметрах, время t – в секундах).
Найти значения  , при которых значения производной функции
, при которых значения производной функции  положительны.
положительны.
Вариант № 3
Найти производную функции:
 ;
;
 ;
;
 ;
;

Найти значение производной функции  в точке
в точке  , если .
, если .
Записать уравнение касательной к графику функции  в точке
в точке  .
.
Точка движется прямолинейно по закону  . Найдите ее ускорение в момент времени
. Найдите ее ускорение в момент времени  (координата
(координата  измеряется в сантиметрах, время t – в секундах).
измеряется в сантиметрах, время t – в секундах).
Найти значения  , при которых значения производной функции отрицательны.
, при которых значения производной функции отрицательны.
Вариант № 4
Найти производную функции:
 ;
;
 ;
;
 ;
;

Найти значение производной функции  в точке
в точке  , если .
, если .
Записать уравнение касательной к графику функции  в точке
в точке  .
.
Точка движется прямолинейно по закону  . Найдите ее скорость в момент времени
. Найдите ее скорость в момент времени  (координата
(координата  измеряется в метрах, время t – в секундах).
измеряется в метрах, время t – в секундах).
Найти значения  , при которых значения производной функции
, при которых значения производной функции  отрицательны.
отрицательны.
Контрольная работа «Применение производной»
Вариант № 1
Найти экстремумы функции: 
Найти промежутки возрастания и убывания функции:
Построить график функции  +3 на отрезке
+3 на отрезке 
Найти наибольшее и наименьшее значения функции на отрезке 
Среди прямоугольников, сумма длин трех сторон у которых равна 20, найти прямоугольник наибольшей площади.
Вариант № 2
Найти экстремумы функции: 
Найти промежутки возрастания и убывания функции: 
Построить график функции  на отрезке
на отрезке 
Найти наибольшее и наименьшее значения функции  на отрезке
на отрезке 
Из всех прямоугольников с диагональю 18 см найдите прямоугольник с наименьшей площадью.
Вариант № 3
Найти экстремумы функции: 
Найти промежутки возрастания и убывания функции: 
Построить график функции  на отрезке
на отрезке 
Найти наибольшее и наименьшее значения функции  на отрезке
на отрезке 
Из всех прямоугольников, площадь которых равна 9см2, найти прямоугольник с наименьшим периметром.
Вариант № 4
Найти экстремумы функции: 
Найти промежутки возрастания и убывания функции: 
Построить график функции  на отрезке
на отрезке 
Найти наибольшее и наименьшее значения функции  на отрезке
на отрезке 
Среди прямоугольников с площадью 25 см2 найдите прямоугольник с наименьшим периметром.
ЭТАЛОНЫ ОТВЕТОВ.
Контрольная работа «Прямые и плоскости в пространстве».
|
| 1 Вариант | 2 Вариант | 3 Вариант | 4 Вариант |
| 1 | 9см | 5 см | 8 см | 1 см |
| 2 | 9,5см | 8,5 см | 10,5 см | 12,5 см |
| 3 | 70°, 110° | 70°, 110° | 80° | 120° |
| 4 | нет | да | да | да |
| 5 | нет | нет | AM | 1 или бесконечное множество |
| 6 | A, B, D | C, D | да | нет |
| 7 | да | 3 | B, C, D | B |
| 8 | скрещивающиеся | a | параллельны | да |
| 9 | пересекаются | плоскость | нет | a, b |
| 10 | прямой | нет | прямая | параллельны |
| 11 | да | нет | 
| BC, AB |
| 12 | (АВС) | 
| да | нет |
| 13 | прямоугольный | да | нет | 
|
| 14 | да | нет | DA, DC | OB |
| 15 | нет | нет | да | да |
| 16 | 90° | с | нет | нет |
| 17 | SD | DB, DC | b, c | прямоугольный |
| 18 | 
| AC | SO | нет |
| 19 | да | нет | да | 
|
| 20 | 4 м | 5 м | 8 м | 15 м |
| 21 |  см см | 60° | 5 см | 8 см |
| 22 | 2 см | 4 см | 4см | 4 см |
| 23 | 12 см |  см см |  см см
| 8 см |
| 24 | 45° | 10 см | 12 см | 6 см |
Контрольная работа «Площади поверхностей и объемы геометрических тел»
|
| 1 Вариант | 2 Вариант | 3 Вариант | 4 Вариант |
|
| Уровень А |
| 1 | 100 см2, 125 см3 | 132 см2 | 240см3 | 75см3 |
| 2 | 450 см3 | 296 см2 | 376 см2 | 280 см2 |
| 3 |  см3 см3
| 80 см3 | 40см3 | 99см3 |
| 4 | 18π см2, 27π см3 | 64π см2, 128π см3 | 18,75π см3 |  см2 см2
|
| 5 | 75π см2 | 50π см2 | 147π см2 | 48π см2 |
|
| Уровень В |
| 6 | 300 см3 | 60 см2 |  см3 см3 |  см3 см3 |
| 7 | 18 см2 | 54 см2 | 108 см2 | 120 см2 |
| 8 | 40π см2 | 40π см3 | 500π см3 | 24π см2 |
| 9 | 8π см3 | 32π см3 |  см3 см3 |  см3 см3 |
|
| Уровень С |
| 10 | 164π см2,  см3 см3 | 676π см2,  см3 см3 | 1156π см2,  см3 см3 | 1600π см2,  см3 см3 |
| 11 | 
| | | |


 Получите свидетельство
Получите свидетельство Вход
Вход



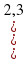 и
и 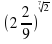
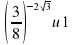
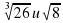
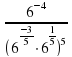
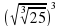
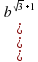
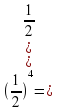
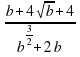
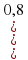 и
и 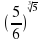
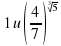
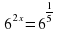
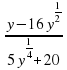
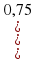 и
и 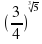









 Контрольно-измерительные материалы для проведения текущего контроля по математике (0.19 MB)
Контрольно-измерительные материалы для проведения текущего контроля по математике (0.19 MB)
 0
0 3182
3182 668
668 Нравится
0
Нравится
0



