Контрольная работа "Тела вращения"

3 вариант(2 уровень)

1. Осевое сечение цилиндра – квадрат, длина диагонали которого равна 15 см. Найдите радиус основания цилиндра

2. Площадь осевого сечения цилиндра равна дм², а площадь основания цилиндра равна 36 дм². Найдите высоту цилиндра.

3. Длина образующей конуса равна 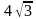см, а угол при вершине осевого сечения конуса равен 120⁰. Найдите площадь основания конуса

4. Стороны треугольника АВС касаются шара. Найдите радиус шара, если АВ=4 см, ВС=6 см, АС=8 см и расстояние от центра шара до плоскости треугольника АВС равно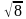

4 вариант(2 уровень)

1. Осевое сечение цилиндра – квадрат, длина диагонали которого равна 8 см. Найдите радиус основания цилиндра

2. Площадь осевого сечения цилиндра равна 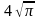дм², а площадь основания цилиндра равна 49 дм². Найдите высоту цилиндра.

3. Высота конуса равна 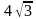см, а угол при вершине осевого сечения конуса равен 120⁰. Найдите площадь основания конуса

4. Стороны треугольника АВС касаются шара. Найдите радиус шара, если АВ=10 см, ВС=12 см, АС=14 см и расстояние от центра шара до плоскости треугольника АВС равно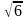

Вариант 1.(1 уровень)

1. Высота конуса равна 96, а диаметр основания — 56. Найдите образующую конуса.

2. Площадь боковой поверхности цилиндра равна , а высота — 8 . Найдите диаметр основания.

3. Диаметр основания конуса равен 60, а длина образующей — 50. Найдите площадь осевого сечения этого конуса.

4. Высота конуса равна 6 см, угол при вершине осевого сечения равен 120⁰. Найдите:

а) площадь сечения конуса плоскостью, проходящей через две образующие, угол между которыми 30⁰; б) площадь боковой поверхности конуса.

5. Осевое сечение цилиндра – квадрат, площадь основания цилиндра равна 16π см². Найдите площадь полной поверхности цилиндра.

Вариант 2.(1 уровень)

1. Высота конуса равна 64, а диаметр основания — 96. Найдите образующую конуса.

2. Площадь боковой поверхности цилиндра равна , а высота — 7 . Найдите диаметр основания.

3. Диаметр основания конуса равен 54, а длина образующей — 45. Найдите площадь осевого сечения этого конуса.

4. Радиус основания конуса равен 6 см, а образующая наклонена к плоскости основания под углом 30⁰. Найдите:

а) площадь сечения конуса плоскостью, проходящей через две образующие, угол между которыми 60⁰; б) площадь боковой поверхности конуса.

5. Осевое сечение цилиндра – квадрат, диагональ которого 4 см. Найдите площадь полной поверхности цилиндра.