Контрольная работа № 1 по теме «Геометрические тела»
I вариант
1. Дана правильная четырехугольная призма.
1.1. Постройте сечение призмы плоскостью, проходящей через диагональ нижнего основания и середину стороны верхнего основания. Установите вид получившегося сечения.
1.2. Вычислите площадь сечения, если боковое ребро призмы равно 4, диагональ основания равна 4![]() .
.
2. Основанием пирамиды является прямоугольный треугольник с катетами 6 и 8. Все боковые ребра пирамиды равны между собой и равны 10. Вычислите углы наклона боковых ребер к основанию.
3. Основания усеченной четырехугольной пирамиды – квадраты, а одно из боковых ребер перпендикулярно основанию. Установите вид всех ее боковых граней и соотношение их площадей, если высота усеченной пирамиды равна h и сторона нижнего основания больше стороны верхнего на h.
II вариант
1. Дана прямая треугольная призма, основанием которой является равнобедренный прямоугольный треугольник.
1.1. Постройте сечение призмы плоскостью, проходящей через гипотенузу верхнего и точку пересечения медиан нижнего основания. Установите вид сечения.
1.2. Вычислите площадь сечения, если гипотенуза основания равна 6, а угол наклона сечения к основанию равен 60.
2. В четырехугольной пирамиде все боковые грани одинаково наклонены к плоскости основания. Основанием пирамиды является квадрат со стороной 8. Вычислите углы наклона боковых граней к основанию, если высота пирамиды равна 4.
3. Усеченная пирамида получена из треугольной пирамиды, основанием которой является равносторонний треугольник, а одной из боковых граней – равнобедренный треугольник, перпендикулярный основанию. Найдите угол наклона большего бокового ребра усеченной пирамиды к основанию, если стороны оснований её равны 2 и 6, а высота усеченной пирамиды равна 6.
Контрольная работа № 2 по теме «Геометрические тела»
I вариант
1. Найдите радиус сечения шара плоскостью, которая проведена на расстоянии от центра, равном трети радиуса шара от его центра. Радиус шара равен a.
2. Развертка боковой поверхности цилиндра – квадрат, площадью 18. Вычислите площадь его осевого сечения. Ответ укажите с точностью до десятых.
3. Конус получен вращением прямоугольного равнобедренного треугольника вокруг оси симметрии. Под каким углом к основанию конуса проходит плоскость, содержащая вершину конуса и хорду основания, отсекающую дугу в 90?
II вариант
1. Три точки, лежащие на поверхности шара, являются вершинами прямоугольного треугольника с гипотенузой 12. На каком расстоянии от центра шара находится плоскость треугольника, если радиус шара равен 10.
2. Из четверти круга, радиусом a, сделали воронку в форме конуса. Во сколько раз образующая конуса будет больше радиуса основания?
3. Осевое сечение цилиндра – квадрат. Найдите отношение площади осевого сечения цилиндра к площади сечения цилиндра плоскостью, параллельной оси цилиндра и отстоящей от нее на расстояние, равное половине радиуса.
Контрольная работа по теме «Тригонометрические функции»
I вариант
1. Построить график функции y = 2 sin x на отрезке ![]() и указать для значений x, принадлежащих этому отрезку:
и указать для значений x, принадлежащих этому отрезку:
– множество значений функции;
– промежутки возрастания и убывания;
– точки максимумов и минимумов функции;
– нули функции;
– участки постоянного знака;
– количество корней уравнения 2 sin x = a в зависимости от a.
2. Дана функция y = sin 2x + 1.
2.1. Определите, обладает ли она свойствами четности, нечетности.
2.2. Докажите, что число является периодом этой функции.
2.3. Укажите промежутки убывания этой функции на отрезке ![]() .
.
3. Расположите числа в порядке убывания:
сos 1,6; cos 40; cos 280; cos 1000.
II вариант
1. Построить график функции y = cos x + 1 на отрезке ![]() и указать для значений x, принадлежащих этому отрезку:
и указать для значений x, принадлежащих этому отрезку:
– множество значений функции;
– промежутки возрастания и убывания;
– точки максимумов и минимумов функции;
– нули функции;
– участки постоянного знака;
– количество корней уравнения cos x + 1 = a в зависимости от a.
2. Дана функция y = 2 cos ![]() .
.
2.1. Исследуйте, обладает ли она свойствами четности, нечетности;
2.2. Докажите, что число 4 является периодом этой функции;
2.3. Укажите промежутки возрастания функции на отрезке [0; 9π].
3. Расположите числа в порядке возрастания:
sin 2; sin50; sin 190; sin 1200.
Контрольная работа № 1 по теме «Начала математического анализа»
I вариант
1. Вычислите производные функций и найдите значение производной в точке x = 1:
y = x5 + 3x3 – 12x2 + ![]() – 18; y =
– 18; y =  ; y =
; y = ![]() sin 2x; y =
sin 2x; y = ![]() ; y = e–x + 1 ln 2x.
; y = e–x + 1 ln 2x.
2. Найдите угловой коэффициент касательной, проведенной к графику функции y = cos 2x в точке с абсциссой x = ![]() .
.
3. Составьте уравнение касательной к графику функции y = x2 – 4, параллельной прямой y = x – 4.
II вариант
1. Вычислите производные функций и найдите значение производной при x = –1:
y = 3x4 – x3 – 3 ∙ ![]() + 5x + 9; y = 6
+ 5x + 9; y = 6![]() –
– ![]() ; y =
; y = ![]() cos 3x; y =
cos 3x; y = ![]() ; y = e2 – x ln (–2x).
; y = e2 – x ln (–2x).
2. Найдите угловой коэффициент касательной, проведенной к графику функции y = sin 0,5x в точке с абсциссой x = ![]() .
.
3. Составьте уравнение касательной к графику функции y = x2 + 2, параллельной прямой y = 2x.
Контрольная работа № 2 по теме «Начала математического анализа»
I вариант
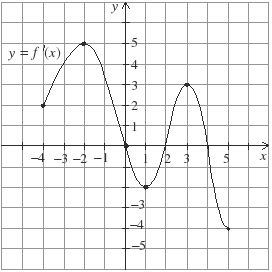
| 1. Дан график производной функции y = f′(x) на отрезке [–4; 5]. Укажите промежутки монотонности и точки экстремумов функции. |
|
2.Докажите, что функция y = ![]() монотонно убывает на каждом интервале, входящем в область определения функции.
монотонно убывает на каждом интервале, входящем в область определения функции.
3. Исследуйте функцию y = ![]() и постройте ее график.
и постройте ее график.
II вариант
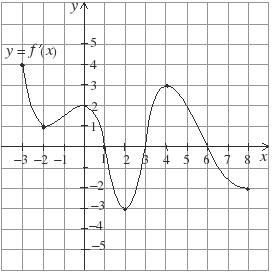
| 1. Дан график производной функции y = f′(x) на отрезке [–3; 8]. Укажите промежутки монотонности и точки экстремумов функции. |
|
2. Докажите, что функция y = ![]() монотонно убывает на каждом интервале, входящем в область определения.
монотонно убывает на каждом интервале, входящем в область определения.
3. Исследуйте функцию y = ![]() и постройте ее график.
и постройте ее график.
Контрольная работа № 3 по теме «Начала математического анализа»
I вариант
1. Проверьте, является ли функция y = –0,2 cos 5x + ![]() – 5x – 7 первообразной функции y = sin 5x –
– 5x – 7 первообразной функции y = sin 5x – ![]() .
.
2. Вычислите первообразную функции y = (2x – 1)4 – x3 – 3x + 1, график которой проходит через точку с координатами (1; 0).
3. Вычислите площадь фигуры, ограниченной линиями: y = 4 – x2, y = 3x, y = 0.
II вариант
1. Проверьте, является ли функция y = 3x2 + 2 ln x – 4 sin 0,5x – 5 первообразной функции y = 6x + ![]() – 2 cos 0,5x?
– 2 cos 0,5x?
2. Найдите первообразную функции y = (2 + 3x)4 – 4x2 + 3x – 2, график которой проходит через точку с координатами (–1; 0).
3. Вычислите площадь фигуры, ограниченной линиями: y = 4x – x2, y = x, y = 0.
Контрольная работа по теме «Измерения в геометрии»
I вариант
1. В цилиндр вписан шар. Найдите, во сколько раз объем цилиндра больше объема шара?
2. Вычислите объем и площадь поверхности прямоугольного параллелепипеда, диагональ которого равна 13, диагональ основания равна 5, а одна из сторон основания равна 3.
3. Вычислите объем и площадь поверхности конуса, разверткой боковой поверхности которого является полукруг с радиусом, равным 2.
II вариант
1. В шар, радиус которого равен 4, вписан цилиндр. Высота цилиндра равна радиусу шара. Найдите, во сколько раз объем шара больше объема цилиндра?
2. У прямоугольного параллелепипеда в основании квадрат со стороной 5![]() . Диагональ параллелепипеда наклонена к основанию под углом 60. Найдите площадь поверхности и объем параллелепипеда.
. Диагональ параллелепипеда наклонена к основанию под углом 60. Найдите площадь поверхности и объем параллелепипеда.
3. Осевое сечение конуса – равносторонний треугольник со стороной 2. Найдите объем и площадь поверхности конуса.
Контрольная работа по теме «Теория вероятности»
I вариант
1. Из 10 первых натуральных чисел случайно выбираются 2 числа. Вычислите вероятности следующих событий.
1.1. Одно из выбранных чисел – единица.
1.2. Оба числа четны.
2. Алфавит состоит из шести букв А, Б, В, Г, Д, Е и четырех цифр 0, 1, 2, 3. Вычислите вероятности следующих событий.
2.1. Случайным образом составленное трехбуквенное слово содержит 2 согласных буквы и одну цифру.
2.2. Случайным образом составленное трехбуквенное слово оказалось четным числом.
3. Внутри квадрата с вершинами (0; 0), (1; 0), (0; 1) и (1; 1) наугад выбирается точка M(x, y). Найдите вероятность события A = {(x; y) | x2 + y2 ≤ a2, a 0}.
II вариант
1. Алфавит состоит из шести букв А, Б, В, Г, Д, Е и четырех цифр 0, 1, 2, 3. Вычислите вероятности следующих событий.
1.1. В случайным образом составленном шестибуквенном слове чередуются буквы и цифры?
1.2. В пятибуквенном слове четыре буквы и цифра 1, причем буквы идут в алфавитном порядке.
2. Из 16 первых натуральных чисел случайно выбираются 2 числа. Вычислите вероятности следующих событий.
2.1. Ни одно из чисел не делится на 3.
2.2. Разность между большим и меньшим из выбранных чисел равна 5.
3. В случайный момент времени x [0; T] появляется радиосигнал длительностью t1. В случайный момент времени y [0; T] включается приемник на время t2 t1. Найдите вероятность обнаружения сигнала, если приемник настраивается мгновенно.
III вариант
1. Класс из 25 учеников можно разбить на 3 группы: 5 отличников, 6 двоечников, остальные учатся на 4 и 3. Выбираем наугад 2 учеников. Вычислите вероятности следующих событий.
1.1. Ученики из разных групп.
1.2. Ни один из них не является отличником.
2. Ученик знает ответы на 15 вопросов из 25. Он может сдавать зачет несколько раз. Предполагается, что его знания остаются на одном уровне и заданный один раз вопрос может быть задан повторно. Вычислите вероятности следующих событий.
2.1. Ученик сдаст зачет со второй попытки.
2.2. Число попыток будет не меньше 6. Пусть заданный один раз вопрос не может быть задан повторно.
2.3. Какова вероятность, что ученик сдаст зачет со второй попытки?
2.4. Какова вероятность, что число попыток будет не меньше 3?
3. Значения a и b равновозможны в квадрате |a| ≤ 1, |b| ≤ 1. Найдите вероятности события A = {корни квадратного трехчлена x2 + 2ax + b положительны}.
Контрольная работа № 1 по теме «Уравнения и неравенства»
I вариант
1. Решите уравнения:
2 cos 4x – 4 cos 2x = 1; ![]() ;
;
25x + 10 5x – 1 – 3 = 0; 11 – x –log2 x = 0;
x2 +9 ![]() = 0.
= 0.
2. Укажите корни уравнения sin2x – 0,5 sin 2x = 0, принадлежащие отрезку ![]() .
.
3. Определите, при каких значениях a уравнение 5х2 + 2ах +5 =0 имеет два различных отрицательных корня?
II вариант
1. Решите уравнения:
2 cos x + 8 sin![]() + 3 = 0;
+ 3 = 0; ![]() ;
;
9x + 3x + 1 – 4 = 0; ![]() ;
;
x2 – 16 ![]() = 0.
= 0.
2. Укажите корни уравнения 2 cos2x – sin 2x = 0, принадлежащие отрезку ![]() .
.
3. Определите, при каких значениях a уравнение х2 + ах + 9 = 0 имеет два различных положительных корня?
Контрольная работа № 2 по теме «Уравнения и неравенства»
I вариант
1. Решите неравенства:
![]() ;
; ![]() x + 1.
x + 1.
2. Найдите целые значения x, удовлетворяющие неравенству: log2 log0,5 (2x – 4) ≤ 2.
3. Решите систему: 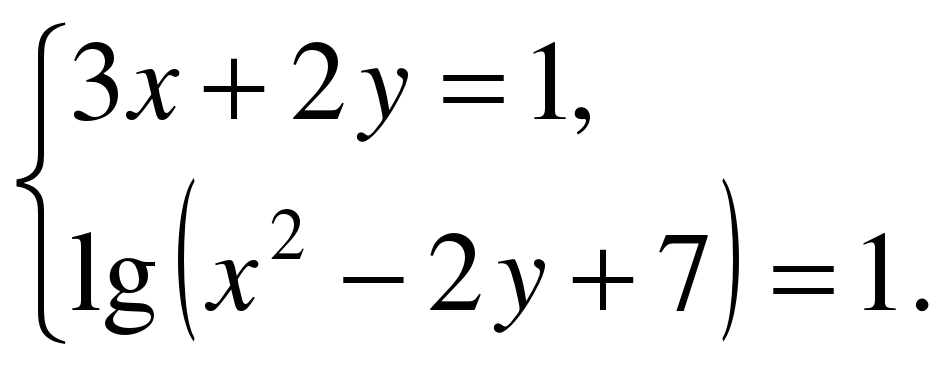 .
.
4. Решите уравнение: |2x – 1| + 6x = |2x – 4| + 15.
5. Определите, при каких целых значениях a система имеет единственное решение, причем x 0, y 0: ![]() .
.
II вариант
1. Решите неравенства:
![]() ;
; ![]()
2. Найдите целые значения x, удовлетворяющие неравенству: ![]() .
.
3. Решите систему: 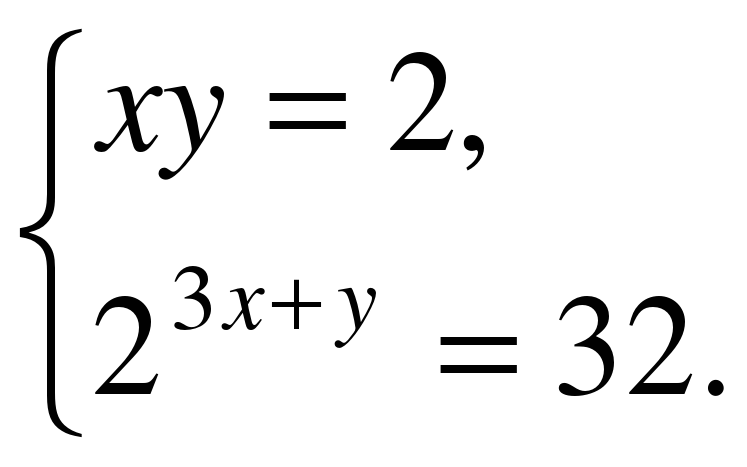
4. Решите уравнение: |x + 1| – 8x = |x – 5| + 4.
5. Определите, при каких целых значениях a система имеет единственное решение, причем x 0, y 0: 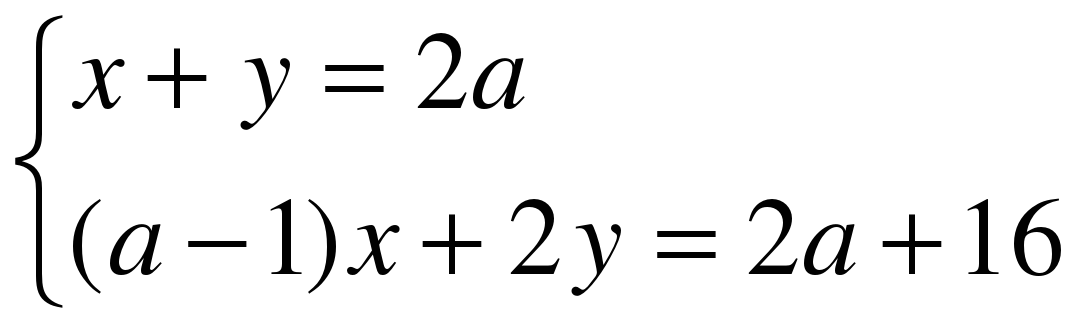 .
.

 Получите свидетельство
Получите свидетельство Вход
Вход











 Контрольная работа (79.45 KB)
Контрольная работа (79.45 KB)
 0
0 1848
1848 40
40 Нравится
0
Нравится
0


