Краткосрочный план
План урока (из опыта учителя)
| Раздел долгосрочного плана: 11.1А Показательные и логарифмические уравнения и неравенства | ГККП «Агротехнический колледж» | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Дата: | ФИО учителя: Башарина Ирина Дмитриевна | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Класс: курс 1 | Количество присутствующих: | отсутствующих: | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Направление | Естественно-математическое | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Тема урока | Показательные уравнения и их системы | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Цели обучения, которые достигаются на данном уроке (ссылка на учебную программу) | 11.2.2.6 - знать и применять методы решения показательных уравнений; 11.2.2.7 - уметь решать системы показательных уравнений; | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Цели урока | Все учащиеся будут:
Большинство учащихся
Некоторые
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Критерии оценивания | Учащийся:
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Языковые цели: | Учащиеся будут: • пояснять методы решения показательных уравнений; • пояснять методы решения системы показательных уравнений; Предметная лексика и терминология:
Серия полезных фраз для диалога/письма:
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Привитие ценностей | Уважение к себе и другим и сотрудничество – через работу в паре, в группе, академическая честность – при самостоятельной работе, открытость – учащиеся самостоятельно могут определить цели урока и задачи. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Связь с предметами | Информатика, физика, химия | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Навыки использования ИКТ | Развивать навыки работы с Active Inspire, Презентация в Power Point. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Предварительные знания | Решение линейных, квадратных, дробно – рациональных уравнений | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Ход урока: | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Запланированные этапы урока | Запланированная деятельность на уроке | Ресурсы | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Начало урока 0 - 3 мин | Приветствие. Психологический настрой: Перекличка с пожеланиями на творческую работу |
Вопросы закрытого типа
Листы с тестовыми вопросами
Слайды
Карточки с заданиями, бумажный и слайдовый материал
Листы с тестами
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Середина урока 4 – 24 мин | Актуализация опорных знаний (студенты предварительно разбиты н группы по 6 человек)
Формативное оценивание тестовых задний Дескрипторы: - определяет вид показательной функции - находит область определения показательной функции - находит область значения показательной функции - определяет график показательной функции по рисунку - использует свойства показательной функции
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Середина урока 25 – 55 мин | Изучение нового материала Эпиграф: Даны ряд уравнений назовите методы их решения: 1) 2) 3) 2х + 5 = 18 – 3х 4) - Чем отличается последнее уравнение от предыдущих (в левой стороне показательная функция) Тема нашего занятия: решение показательных уравнений и их систем. Мотивация. Многие задачи физики, химии решаются как показательные уравнения. Так например, Чтобы масса бактерий была равна 30 г, необходимо, чтобы прошло Wt= 20 · Опред. Показательным уравнение называют уравнение вида Например: Показательные уравнения после тождественных преобразований приводят к виду Если в Рассмотрим способы решения уравнений: (Работа на доске и в тетрадях вместе с учителем)
Примеры:
2 способ. Вынесение общего множителя за скобки
3способ. Введение новой переменной. 4 способ. Деление обеих частей уравнения на показательную функцию
5 способ. Графический способ решения
Решение систем уравнений
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Середина урока
56 – 85 мин | Закрепление изученного материала (работа в группах) Базовый уровень 1. 2. 3.
Средний уровень («Подумай, реши, поделись мыслями»)
Продвинутый уровень (метод «Объясни, спроси, проверь»)
ТЕСТ «Показательные уравнения» (приложение 4) Задания теста представлены в двух уровнях. Ӏ уровень – это задания на 1 – 2 шага. Для ответа на них учащимся достаточно знать правила, формулы, простейшие зависимости между компонентами математических действий. ӀӀ уровень включает более сложные задания на 2 – 4 шага, а их решение требует более широкого круга математических знаний, умений и навыков. Задания Ӏ уровня оцениваются: за правильный ответ выставляется 1 балл, за неправильный ответ – 0 баллов. На ӀӀ уровне: - за правильный ответ с письменными записями, которые не содержат ошибок, 2 балла; - за неполный или неправильный ответ, но имеется письменное решение, содержащее верный ход решения, выставляют 1 балл; - в остальных случаях 0 баллов.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Конец урока
86 - 90 мин | Домашнее задание. Подобрать и решить уравнения, решаемые 1-3 способами (3 уравнения) В конце урока рефлексия. Ответьте на вопросы: -почему уравнение вида -где в будущей профессии может пригодится составление и решение показательных уравнений
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Дифференциация – каким образом Вы планируете оказать больше поддержки? Какие задачи Вы планируете поставить перед более способными учащимися? | Оценивание – как Вы планируете проверить уровень усвоения материала учащимися? | Здоровье и соблюдение техники безопасности | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Дифференциация заключается в оказании индивидуальной поддержки учащемуся через подбор учебного материала и ресурсов с учетом индивидуальных способностей. | Взаимооценивание и самооценивание индивидуальной, групповой деятельности учащихся по разработанным дескрипторам. | Учитывать влияние освещения в классной комнате на зрение учащихся. Рационально по времени использовать интерактивную доску. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Приложение 1
Устный опрос: к уроку «Показательные уравнения»
1) какая функция называется показательной функцией?
2) какие из приведенных функций являются показательными
f(x) = ; f(x) = ; ?
3) назовите основание показательной функции
4) перечислить основные свойства данных функций
- область определения
- область значения
- какие из данных функций являются возрастающими, убывающими?
- какому рисунку соответствует график каждой из функций
5) укажите множество значений функций
f(x) =
f(x) = – 3
Приложение 2
Задания для групповой работы:
Выполнить соответствие, к результатам применить шифратор
1 группа. Представьте в виде степени с основанием 2
| 1 | -4 |
| 8 | -3 |
|
| -1 |
| 32 | 0 |
|
|
|
|
| 3 |
|
| 5 |
Шифратор
| -4 | -3 | -1 | 0 |
| 3 | 5 |
| М | Х | Е | А | Д | Р | И |
-
Группа. Возвести в степень
|
|
|
|
|
|
|
| 1 |
|
|
|
|
| 2 |
|
| 4 |
|
| 9 |
Шифратор
|
|
| 1 |
| 2 | 4 | 9 |
| А | П | Ф | О | Р | Г | И |
-
Группа. Вычислить.
| lg2 +lg500
| -1 |
|
| 0 |
|
| 1 |
|
| 2 |
|
| 3 |
|
| 4 |
|
|
|
|
|
|
|
|
|
| -1 | 0 | 1 | 2 | 3 | 4 |
| Н | В | М | О | Л | С |
Приложение 3.
Тест. Показательная функция
1 вариант
-
Какая из перечисленных функций является показательной функцией
-
f(x) = 5х
-
f(x) =
-
f(x) =
-
f(x) = 4
-
f(x)=
-
Выбрать область определения функции f(x) =
-
Х
R
-
-
х
-
х
-
х
-
какому промежутку принадлежит область значения функции f(x)= (
-
у
-
у
-
у
-
у
-
у
-
Какой из графиков является графиком функции f(x) = (
-
1
-
-
-
-
1 2
-
-
-
-
-
-
-
-
3 4
5.Сравнить значение m и n
(
-
m
m
m
4) m
m = n
Тест. Показательная функция
-
вариант
-
Какая из перечисленных функций является показательной функцией
-
f(x) = 3х
-
f(x) =
-
f(x) =
-
f(x) = 2
-
f(x)=
-
Выбрать область определения функции f(x) =
-
-
х
-
х
-
Х
R
-
х
-
какому промежутку принадлежит область значения функции f(x)= (
-
у
-
у
-
у
-
у
-
у
-
Какой из графиков является графиком функции f(x) = (
-
1
-
-
-
-
1 2
-
-
-
-
-
-
-
-
3 4
5.Сравнить значение m и n
(
-
m
m
m
m
m = n
Тест. Показательная функция
-
вариант
1. Какая из перечисленных функций является показательной функцией
1) f(x) = 7х
2) f(x) =
3) f(x) =
-
f(x) = 7
-
f(x)=
2. Выбрать область определения функции f(x) =
2) х
3) х
4) х
5)Х R
3. какому промежутку принадлежит область значения функции f(x)= (
-
у
-
у
-
у
-
у
-
у
4. Какой из графиков является графиком функции f(x) = (
-
1
-
-
-
-
1 2
-
4
5.Сравнить значение m и n
(
-
m
m
m
m
m = n
Тест. Показательная функция
-
вариант
1.Какая из перечисленных функций является показательной функцией
-
f(x) = 5х
-
f(x) =
-
f(x) =
-
f(x) = 3
-
f(x)=
2. Выбрать область определения функции f(x) =
2) х
3) х
4) Х R
5) х
3. какому промежутку принадлежит область значения функции f(x)= (
-
у
-
у
-
у
-
у
-
у
4.Какой из графиков является графиком функции f(x) = (
-
1
-
-
-
-
1 2
-
-
-
-
-
-
-
-
3 4
5.Сравнить значение m и n
(
-
m
m
m
m
m = n
Тест. Показательная функция
-
вариант
-
Какая из перечисленных функций является показательной функцией
-
f(x) = 2х
-
f(x) =
-
f(x) =
-
f(x) = 8
-
f(x)=
-
Выбрать область определения функции f(x) =
-
х
-
х
-
Х
R
-
х
-
какому промежутку принадлежит область значения функции f(x)= (
-
у
-
у
-
у
-
у
-
у
-
Какой из графиков является графиком функции f(x) = (
-
1
-
-
-
-
1 2
-
-
-
-
-
-
-
-
3 4
5.Сравнить значение m и n
(
-
m
m
m
m
m = n
Тест. Показательная функция
-
вариант
1. Какая из перечисленных функций является показательной функцией
-
f(x) = 3+х
-
f(x) =
-
f(x) =
-
f(x) = 3
-
f(x)=
2. Выбрать область определения функции f(x) =
-
х
-
х
-
Х
R
-
х
3. какому промежутку принадлежит область значения функции f(x)= (
-
у
-
у
-
у
-
у
-
у
4. Какой из графиков является графиком функции f(x) = (
-
-
-
4
5.Сравнить значение m и n
(
-
m
m
m
m
m = n
Приложение 4.
Тест. Решение показательных уравнений.
Ӏ уровень
1) Найти х, если =
.
А) 1; Б) 0; В) -1; Г) 2; Д) -2.
2) Найти корень уравнения = 64.
А) 4; Б) 3; В) 2; Г) 1; Д) 0.
3) Решить уравнение .
А) 0; Б) 3; В) 1; Г) -1; Д) 4.
4) При каком значении х
А) 2; Б) 0; В) -2; Г) 1; Д) -1.
5) Решить уравнение .
А) 1; Б) ; В)
; Г)
; Д)
.
6) Найти х, если .
А) 5; Б) 4; В) 6; Г) -4; Д) -6.
7) При каком значении х ?
А) -3; Б) 1; В) -2; Г) 2; Д) 3.
8) Решить уравнение .
А) 7; Б) 4; В) 1; Г) 5; Д) 2.
ӀӀ уровень
1) Найти х, если
А) 2; Б) 1; В) -1; Г) -2; Д) -3.
2) Указать число, которое является корнем уравнения
.
А) 3; Б) 4; В) 2; Г) -2; Д) -3.
3) Решить уравнение .
А) 3; Б) 1; В) 4 Г) -1; Д) 2.
4) При каком значении х ?
А) 3; Б) ; В)
; Г) 2; Д) 1.
5) Решить уравнение .
А) ; Б)
; В)
; Г) 0; Д) 1.
6) Найти х, если .
А) ; Б)
; В)
; Г) 4; Д) - 4.
7) Решить уравнение .
А) -1; Б) 1; В) -2; Г) 2; Д) 3.
7) Указать число, которое является корнем уравнения
А) 3; Б) -1; В) -2; Г) 2; Д) -3.

 Получите свидетельство
Получите свидетельство Вход
Вход




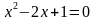
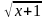 = 4
= 4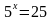
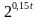 = 30
= 30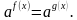 а
а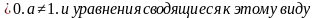
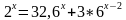 =16,
=16, 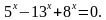
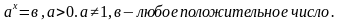
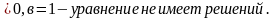
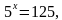 2)
2) 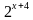 =8, 3) (
=8, 3) ( 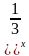 =81
=81 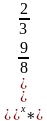
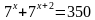 2)
2) 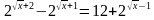
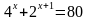
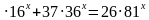
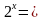 5
5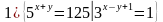
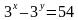
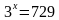
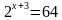
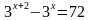









 Конспект занятия " Показательные уравнения" (248.58 KB)
Конспект занятия " Показательные уравнения" (248.58 KB)
 0
0 78
78 3
3 Нравится
0
Нравится
0




