Конспект урока: теорема Виета

УЧИТЕЛЬ: Д. П. АЛИМАСОВА АЛГЕБРА 8 КЛАСС УРОК № 52 23.01.2019

ТЕМА: ТЕОРЕМА ВИЕТА

Тип урока: урок изучения нового материала

Цель: создать условия для формирования у учащихся навыка решения квадратного уравнения с использованием теоремы Виета.

Планируемые результаты: учащийся научится: оперировать на базовом уровне понятиями: квадратное уравнение, корень квадратного уравнения, решение квадратного уравнения; проверять, является ли данное число решением уравнения; решать квадратные уравнения по формуле корней квадратного уравнения; составлять план решения задачи; выделять этапы решения задачи; учащийся получит возможность научиться: оперировать понятиями: квадратное уравнение, корень квадратного уравнения, составлять и решать квадратные уравнения, уравнения, к ним сводящиеся при решении задач других учебных предметов.

Оборудование: конспект урока, учебники, карточки с домашним заданием, компьютерная презентация.

Формы обучения: фронтальная, парная.

ХОД УРОКА

I. Организационный этап (1 мин)

Приветствие, проверка готовности к уроку. Проведение инструктажа.

II. Проверка домашнего задания (5 мин)

Фронтальный опрос по домашнему заданию (сверить полученные ответы в ходе решения уравнений из домашнего задания)

III. Целеполагание и мотивация учебной деятельности учащихся (2 мин)

Ребята, у нас сегодня будет очень важная тема. На прошлом занятии мы с Вами рассматривали особый вид уравнения и один из методов его решения. Сегодня рассмотрим еще один способ решения данного уравнения. Для того, чтобы усвоить эту тему что вам нужно делать? Зачем вам это нужно? Что необходимо делать, чтобы получить желаемый результат?

IV. Оглашение темы урока (1 мин)

СЛАЙД 1. Итак, тема урока «Теорема Виета». В связи с тем, что это новая тема, то у меня есть вопрос: верите ли Вы в то, что в конце этого урока каждый из вас сможет усвоить данную тему? Верите ли вы в то, что каждый из вас, при условии, что будет активно работать на уроке, сможет самостоятельно решить квадратное уравнение с помощью теоремы Виета? Верите ли вы в то, что каждый из вас в результате усвоенных знаний сможет с легкостью выполнить домашнее задание? Итак, приступим.

V. Актуализация опорных знаний и умений учащихся (7 мин)

СЛАЙД 2. Провести в виде беседы опрос по ключевым моментам прошлого урока:

Что такое приведенное квадратное уравнение?

Вспомним стандартный вид квадратного уравнения:

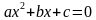
Если в этом уравнении каждое слагаемое поделить на число a, т.е. на число, стоящее перед 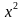, то у нас получится приведенное квадратное уравнение:

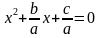
Т.е., приведенное квадратное уравнение – это уравнение, в котором перед старшим неизвестным стоит число 1, т.е. коэффициент равен 1. В таких случаях уравнение чаще всего записывают в таком виде:

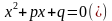
Под буквой 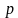подразумевается 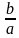, под буквой - .

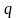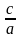СЛАЙД 3. О чем же говорит теорема Виета? Теорема Виета утверждает, что если есть корни квадратного уравнения (*), числа 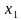и 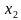, то в случае, если мы их сложим, то получим число противоположное числу 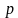, т. е. противоположное коэффициенту, стоящему при x. А если мы их перемножим, то получим число 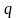, т.е. число равное свободному члену уравнения:

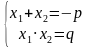
Данное утверждение и есть теорема Виета. Тут фигурная скобка показывает, что оба этих условия происходят одновременно. Существует так же обратная теорема Виета. В ней говорится, что если существуют какие-то два числа, такие, что их сумма будет равняться второму коэффициенту с противоположным знаком, а произведение – свободному члену, то эти два числа обязательно будут являться корнями этого квадратного уравнения. Обычно, не разделяют понятия «прямая» и «обратная» теорема Виета. Говорят просто: по теореме Виета. Некоторые люди умеют мгновенно находить корни квадратного уравнения, пользуясь теоремой Виета. Вам будет интересно узнать, как они это делают. Я сейчас вам открою этот секрет. Это не сложно, если к этому привыкнуть. Итак, давайте попробуем найти корни квадратного уравнения по теореме Виета. Подчеркну, что для использования теоремы Виета необходимо использовать очень важное условие: необходимо знать наверняка есть ли у уравнения корни. Т.е., что дискриминант больше или равен нулю.

Попробуем подобрать корни для такого уравнения:

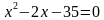
(уравнение записывается на доску, один человек к доске, остальные в тетрадях)

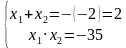
Давайте помечтаем. Какие числа нам при умножении друг на друга могут дать 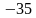? Это числа: 5 и -7, -5 и 7, 1 и -35, -1 и 35. Эти 4 комбинации мы с вами в уме сейчас быстренько и проверим. А проверять мы их будем, подставляя эти пары в равенство: 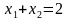. Т. о., ответом будет -5 и 7.

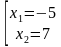
Ответ: -5 и 7.

Итак, если привыкнуть к применению теоремы Виета для решения квадратных уравнений, то на процесс нахождения решения будет уходить меньше времени, чем при применении формул нахождения корней квадратного уравнения.

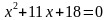
(уравнение записывается на доску, один человек к доске, остальные в тетрадях)

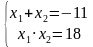
Давайте помечтаем. Какие числа нам при умножении друг на друга могут дать 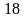? Это числа: 1 и -18, -18 и -1, 9 и 2, -2 и -9, 3 и 6, -6 и -3. Эти 6 комбинаций мы с вами в уме сейчас быстренько и проверим. А проверять мы их будем, подставляя эти пары в равенство: 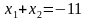. Т. о., ответом будет -2 и -9.

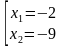
Ответ: -2 и -9.

VI. Первичное закрепление в знакомой ситуации (типовые) в измененной ситуации (конструктивные) (4 мин):

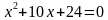
(учащиеся пытаются решить самостоятельно, затем один человек к доске, остальные проверяют полученное ими решение)

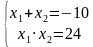
Существует много пар чисел, которые дают нам произведение 24. Мы их сейчас выпишем, обычно это делается в уме, и проверим какие из них дают в сумме -10. Числа: 1 и 24, -1 и -24, 2 и 12, -2 и -12, 4 и 6, -4 и -6, 3 и 8, - 3 и -8. Проверяем все эти комбинации, подставляя их будем в равенство: . Т. о., ответом будет -4 и -6.

Ответ: -4 и -6.

Все эти переборы делаются в уме. Если немного потренироваться, то можно все это решать быстро.

VII. Творческое применение и добывание знаний в новой ситуации (проблемные задания) (21 мин)

Есть один очень важный момент, о котором мы еще не упоминали и сейчас Вы о нем узнаете. Рассмотрим такое уравнение:

Если использовать теорему Виета, то должно выполнятся условие:

Т. е. сумма корней должна быть равна 1, а произведение 12. Но подобрать такие числа не выйдет. Потому, что корней просто не существует. Убедимся в этом, найдя дискриминант:

Т.е. корней нет. Теорема Виета для этого уравнения не применима.

Рассмотрим еще несколько заданий, в которых применяется теорема Виета.

СЛАЙД 4.

1. Составление квадратного уравнения с данными корнями

Нам даны корни:

Нужно составить квадратное уравнение с этими корнями.

(один человек у доски, остальные в тетрадях. Выполняем задание с комментариями и наводящими вопросами, приводящими к решению задачи)

Для этого находим число p, которое будет равняться противоположному числу сумме этих двух чисел.

Находим число q:

Получив эти числа, мы составляем приведенное квадратное уравнение:

СЛАЙД 5.

1. Составление квадратного уравнения с данными корнями.

Отличие от предыдущего в том, что корнями уравнения являются дробные числа.

Нужно составить квадратное уравнение с этими корнями.

(один человек у доски, остальные в тетрадях. Выполняем задание с комментариями и наводящими вопросами, приводящими к решению задачи)

Для этого находим число p, которое будет равняться противоположному числу сумме этих двух чисел.

Находим число q:

Получив эти числа, мы составляем приведенное квадратное уравнение:

Умножаем все слагаемые данного уравнения на 3. Получаем более элегантное уравнение:

Именно в таком виде принято записывать квадратное уравнение, составленное с помощью корней.

Следующий вид в котором используется теорема Виета, это задание в котором сообщается один из корней и указывают на уравнение в котором не хватает одного из коэффициентов.

СЛАЙД 6.

1. Найти недостающий коэффициент и второй корень уравнения:

Выписываем теорему Виета:

И нам остается выписать ответ:

б)

Выписываем теорему Виета:

И нам остается выписать ответ:

Ответ:

в)

Сначала перепишем квадратное уравнение в виде приведенного квадратного уравнения:

Выписываем для полученного уравнения теорему Виета:

И нам остается выписать ответ:

Ответ:

СЛАЙД 7.

4. Есть еще один вид заданий. В нем не дается ни первого корня, ни которого, а лишь сообщается, что один из них на 11 больше другого:

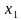на 11 больше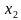

Выписываем для полученного уравнения теорему Виета:

Отдельно записываем, что первый корень больше второго на 11:

Мы получили три уравнения. Т.к. все эти условия должны выполняться одновременно, то мы можем выбрать те 2 уравнения, которые позволят нам найти искомые корни:

Из 7 класса мы знаем как решаются системы методом подстановки. Имеем:

Теперь найдем m:

Для этого вспомним, что у нас есть еще и третье уравнение из системы:

Ответ:

СЛАЙД 8.

VI. Сообщение домашнего задания и инструктаж (2 мин)

№ 585, 588, 594 (б, в, г), 595 (а, в, г)

VII. Рефлексия (2 мин)

СЛАЙД 9. Шел мудрец, а навстречу ему три человека, везли под горячим солнцем тележки с камнями для строительства Храма. Мудрец остановился и задал каждому по вопросу. У первого спросил: - Что ты делал целый день? И тот с ухмылкою ответил, что целый день возил проклятые камни. У второго спросил: «А ты что делал целый день?» - И тот ответил: «Я добросовестно выполнял свою работу». А третий улыбнулся его лицо засветилось радостью и удовольствием и он ответил «А я принимал участие в строительстве Храма»

-Ребята! Кто работал так как первый человек?

-Кто работал добросовестно?

-А кто принимал участие в строительстве Храма знаний? (Оцените себя)

5